Chapter: Mathematics (maths) : Fourier Transforms
Important Questions and Answers: Fourier Transforms
FOURIER TRANSFORMS
PART
–A
1. State Fourier integral theorem.
If f(x) is piece-wise continuously differentiable and absolutely integrable in (- ¥, ¥) then
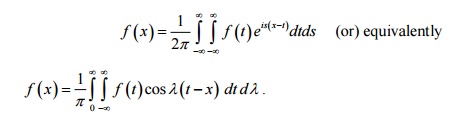
This
is known as Fourier integral theorem or Fourier integral formula.
2. Define Fourier transform pair (or)
Define Fourier transform and its inverse transform.
The complex (or infinite) Fourier transform of f(x)
is given by
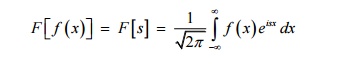
Then the function f(x) is the inverse Fourier
Transform of F(s) and is given by
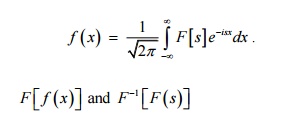
its also called Fourier Transform
Pairs.
3. Show
that f(x) = 1, 0 < x < ¥
cannot be represented by a Fourier integral.
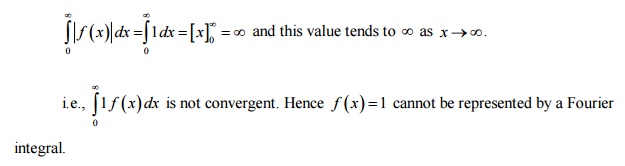
4. State and prove the linear property
of FT.
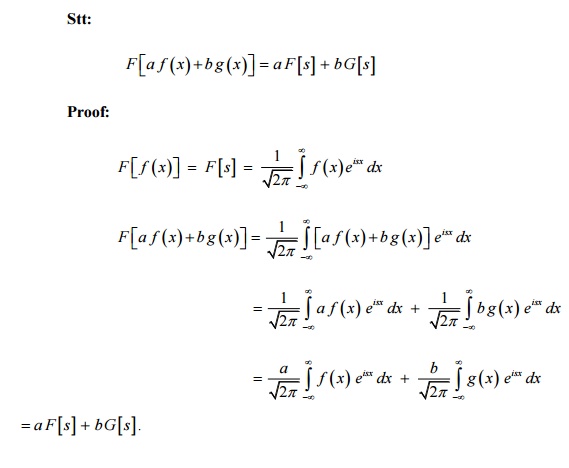
5. State and prove the Shifting property of FT.
Stt:
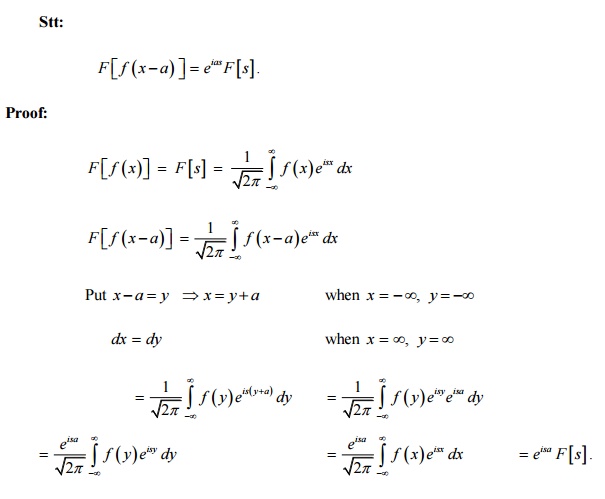
6. State and prove the Change of scale property of FT.
Stt:


8. State and prove the Modulation
property of FT. (OR) If Fourier transform of f(x) is F(s).
Prove that the Fourier transform of f
(x)cos ax is
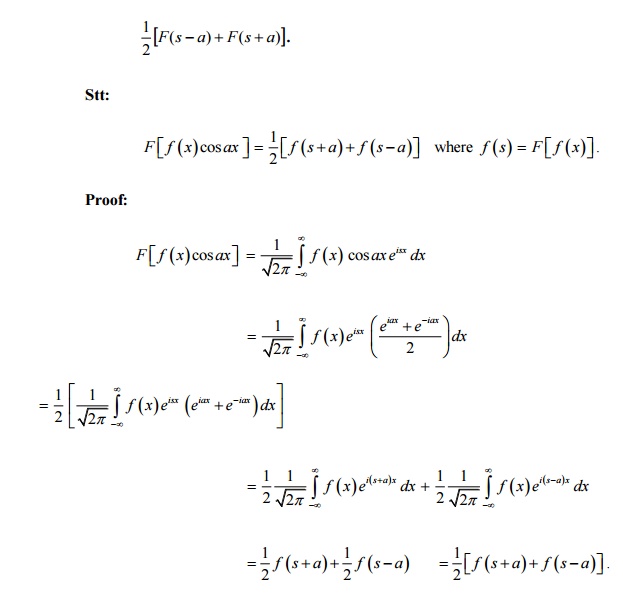
9. What is meant by self-reciprocal with
respect to FT?
If
the Fourier transform of f (x)is
obtained just by replacing x by s, then f
(x)is called
self-reciprocal with respect to FT.
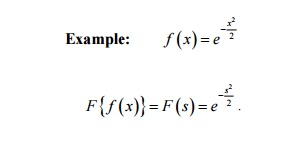

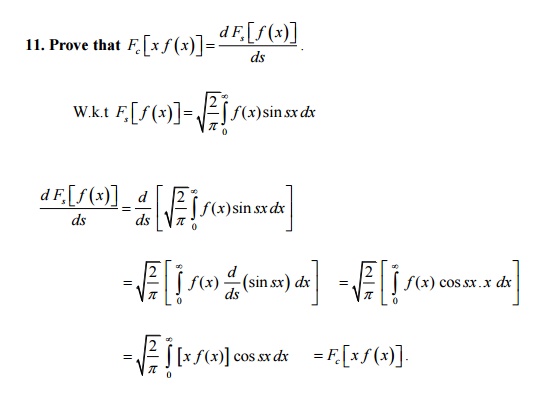
12. Define Fourier cosine transform
(FCT) pair.
The infinite Fourier cosine transform of f(x) is
defined by

13.
Find the Fourier Cosine transform
of f(x) =
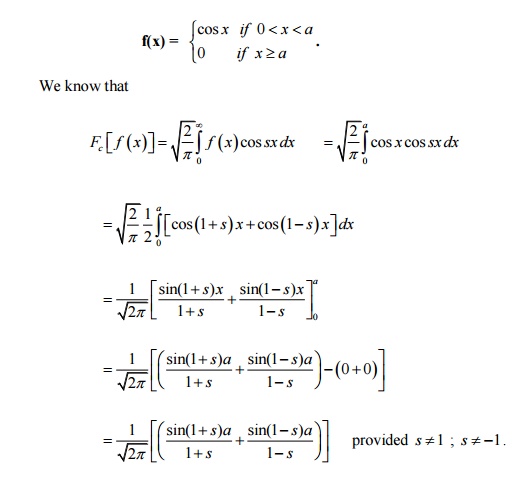
14. Find the Fourier Cosine transform of
e-ax , a > 0.
Given f
(x)=e-ax
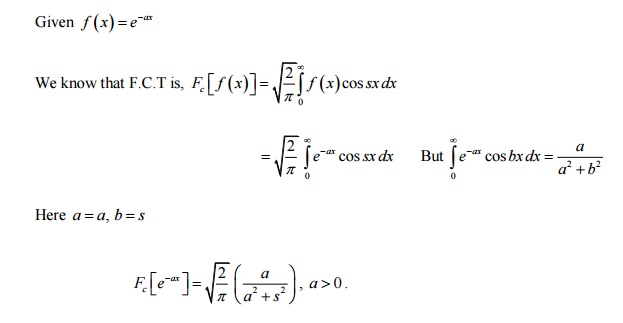
15. Find the Fourier Cosine transform of
e-x
.
We know that
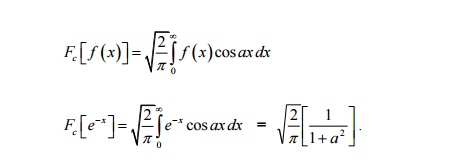
16. Define Fourier sine transform (FST)
pair.
The infinite Fourier sine transform of f(x) is
defined by

17.
Find the Fourier Sine transform of e-3x
.
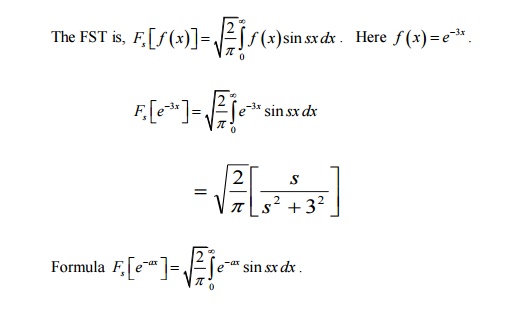
18.
Find the Fourier Sine transform of
f(x)= e-x
.
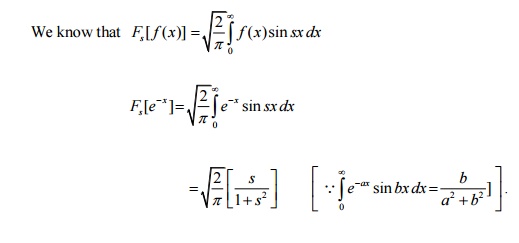
19. Find the Fourier Sine transform of 3e-2 x
.
Let f (x)=3e-2 x

20.
Find the Fourier Sine transform of
1/x.
We know that
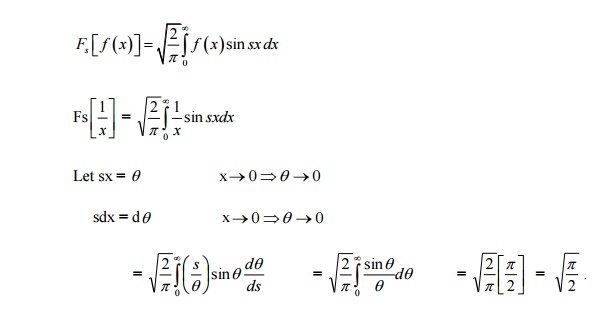
21.
State the Convolution theorem on
Fourier transform.

22.State
the Parseval’s formula or identity
If F s is the Fourier transform of
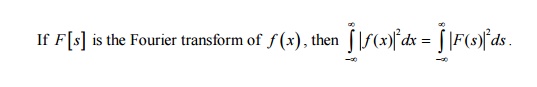
PART
B
1. State and prove the convolution
theorem for Fourier Transforms.
Statement:

PROOF: By convolution
of two functions:

F[( f *g
)(x)]=F(s)G(s)

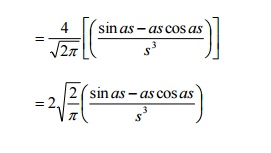
3. Show that e x2/2 is
reciprocal with respect to Fourier transforms
Solution:
Fourier transform:




6. Find the Fourier cosine transform of e-a2
x2
Solution:
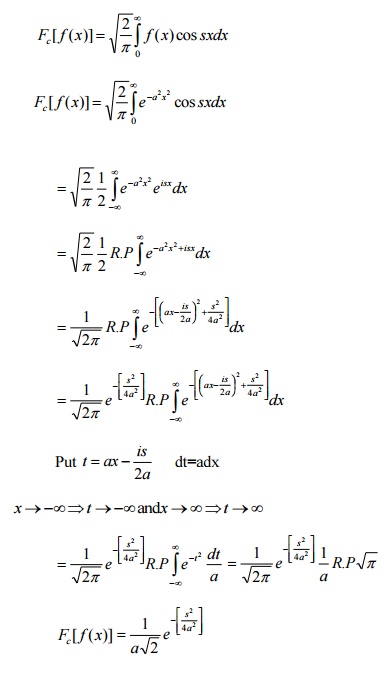




Related Topics