Chapter: Mathematics (maths) : Fourier Transforms
Fourier Transforms
FOURIER TRANSFORMS
1 INTRODUCTION
2 INTEGRAL TRANSFORMS
3 FOURIER INTEGRAL THEOREM
4 FOURIER TRANSFORMS AND ITS PROPERTIES
5 CONVOLUTION THEOREM AND PARSEVAL’S
THEOREM
6 FOURIER SINE AND COSINE TRANSFORMS
1 Introduction
This unit starts with integral
transforms and presents three well-known integral transforms, namely, Complex
Fourier transform, Fourier sine transform, Fourier cosine transform and their
inverse transforms. The concept of Fourier transforms will be introduced after
deriving the Fourier Integral Theorem. The various properties of these
transforms and many solved examples are provided in this chapter. Moreover, the
applications of Fourier Transforms in partial differential equations are many
and are not included here because it is a wide area and beyond the scope of the
book.
2 Integral Transforms
The integral transform f(s) of a
function f(x) is defined by
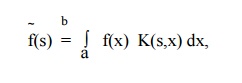
if the integral exists and is denoted by I{f(x)}. Here, K(s,x) is called the kernel of the transform. The kernel is a known function of „s‟ and „x‟. The function f(x) is called the inverse transform of f(s). By properly selecting the kernel in the definition of general integral transform, we get various integral transforms.
The following are some of the well-known transforms:
(i) Laplace Transform
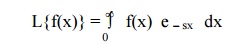
(ii)
Fourier Transform
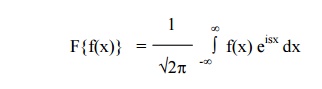
(iii) Mellin Transform
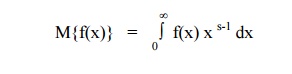
(iv) Hankel Transform
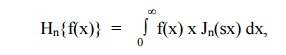
where Jn(sx) is the Bessel function of the first kind and order 'n'.
3
FOURIER INTEGRAL THEOREM
If f(x) is defined in the interval (-ℓ,ℓ), and the following conditions
(i) f(x) satisfies the Dirichlet‟s conditions in every interval (-ℓ,ℓ),


which is known as the Fourier integral of
f(x).
Note:
When f(x) satisfies the
conditions stated above, equation (3) holds good at a point of continuity. But
at a point of discontinuity, the value of the integral is (1/ 2) [f(x+0) +
f(x-0)] as in the case of Fourier series.
Fourier sine and cosine Integrals
The Fourier integral of f(x) is given by
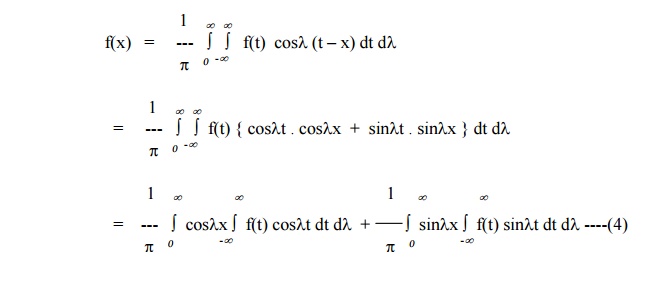
When f(x) is an odd function, f(t) coslt is odd while f(t) sinlt is even. Then the first integral of (4) vanishes
and, we get
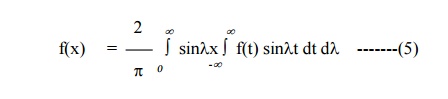
which is known as the Fourier sine integral.
Similarly, when f(x) is an even
function, (4) takes the form
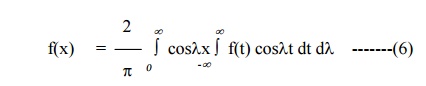
which is known as the Fourier cosine integral.
Complex form of Fourier Integrals
The Fourier integral of f(x) is given by
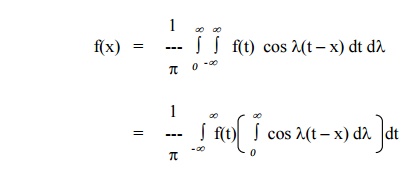
Since cos l(t
–x) is an even function of l,
we have by the property of definite integrals
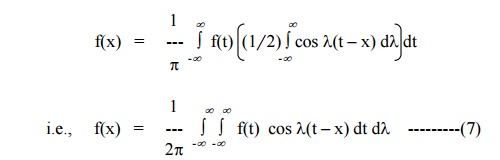
Similarly, since sin l(t
–x) is an odd function of l,
we have
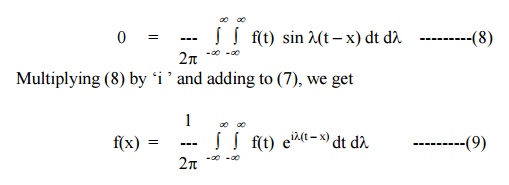
which is the complex form of the Fourier
integral.
4
Fourier Transforms and its properties
Fourier Transform
We know that the complex form of Fourier
integral is

The function F(s),
defined by (1), is called the Fourier Transform of f(x). The function
f(x), as given by (2), is called the inverse Fourier Transform of F(s).
The equation (2) is also referred to as the inversion formula.
Properties of Fourier Transforms
(1) Linearity Property
If
F(s) and G(s) are Fourier Transforms of f(x) and g(x) respectively, then
F{a f(x) + bg(x)} = a F(s) + bG(s),
where a and b are constants.
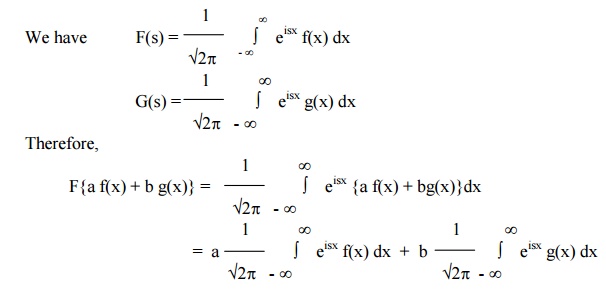
= a F(s) + bG(s) i.e,
F{a f(x) + bg(x)} = a F(s) + bG(s)
(2) Shifting
Property
(i)
If
F(s) is the complex Fourier Transform of f(x), then
F{f(x-a)} = eisa F(s).

(ii) If F(s) is the complex Fourier
Transform of f(x), then

(3) Change of scale property
If F(s) is the complex Fourier transform
of f(x), then
F{f(ax)} =1/a F(s/a), a ¹0.
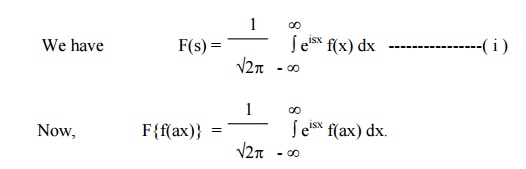
Put
ax = t, so that dx = dt/a.
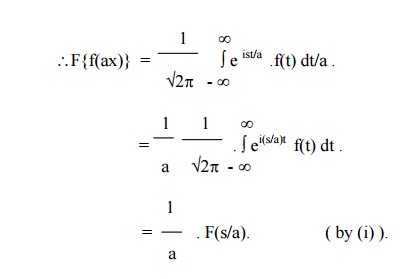
(4) Modulation theorem.
If F(s) is the complex Fourier transform
of f(x),
Then F{f(x) cosax} = ½{F(s+a) + F(s-a)}.

(5) nth derivative of the
Fourier Transform
If F(s) is the complex Fourier Transform of f(x),
Then F{xn f(x)} = (-i)n
dn/dsn .F(s).

(6) Fourier Transform of the derivatives
of a function.
If
F(s) is the complex Fourier Transform of f(x),
Then, F{f-isF(s) if„(x)}f(x)®0as x=® ±¥.


In general, the Fourier transform of the
nth derivative of f(x) is given by
F{f n(x)} = (-is)n
F(s),
provided-1 ‟the derivatives frst®„n±¥. vanish
as x
Property (7)
If F(s) is the complex Fourier Transform
of f(x), then F

Property (8)
If F(s) is the complex Fourier transform
of f(x),

Note: If F{f(x)} = F(s), then
F{f(-x)} = F(-s).
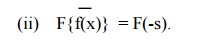
Example
1
Find the F.T of f(x) defined by
f(x) = 0 x<a
= 1 a<x<b
= 0 x>b.
The F.T of f(x) is given by
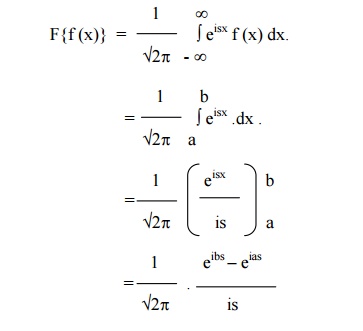
Example 2
Find the F.T of f(x) = x for |x
| =< a
= 0 for
|x | > a.

Example 3
Find the F.T of f(x) = eiax , 0 < x < 1
= 0 otherwise
The F.T of f(x) is given by
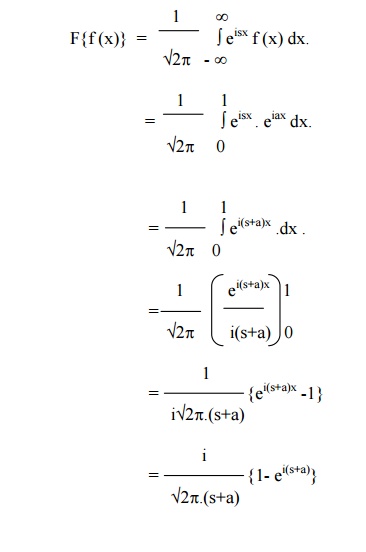

Note:
If the F.T of f(x) is f(s), the function
f(x) is called self-reciprocal. In the above example
e -x 2/ 2 is self-reciprocal under F.T.
Example 5
Find the F.T
of
f(x) = 1 for |x|<1.
= 0 for |x|>1.



5 Convolution Theorem . and Parseval’s Theorem
The convolution of two functions f(x)
and g(x) is defined as
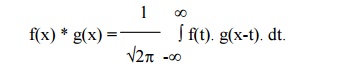
Convolution
Theorem for Fourier Transforms.
The Fourier Transform of the convolution
of f(x) and g(x) is the product of their Fourier Transforms,
i.e,
F{f(x) * g(x)} = F{f(x).F{g(x)}.
Proof:
F{f(x) * g(x)} = F{(f*g)x)}

Hence, F{f(x) * g(x)} = F{f(x).F{g(x)}.
Parseval’s
identity for Fourier
Transforms
If
F(s) is the F.T of f(x), then
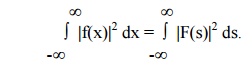
Proof:
By convolution theorem, we have
F{f(x)
* g(x)} = F(s).G(s).
Therefore, (f*g) (x) = F-1{F(s).G(s)}.

Example
6
Find
the F.T of f (x) = 1-|x|for |x|<1.
=
0 for |x|> 1


Example
7
Find the F.T of f(x) if
f(x) =
= 1 for |x|<a
=
0 for |x|>a>0.

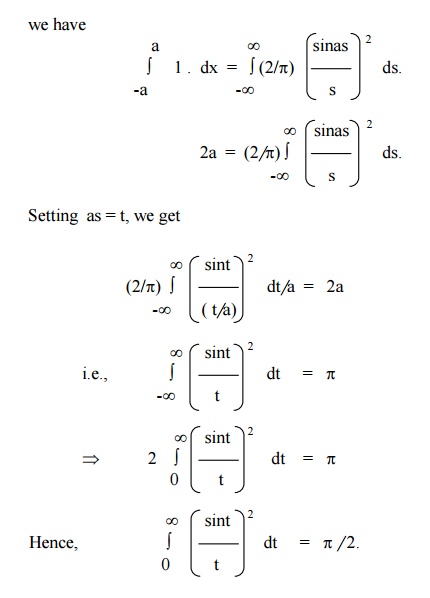
6 Fourier sine and cosine transforms:
Fourier sine Transform
We know that the Fourier sine integral
is

The function Fs(s),
as defined by (1), is known as the Fourier sine transform of f(x). Also
the function f(x), as given by (2),is called the Inverse Fourier sine
transform of Fs(s) .
Fourier cosine transform
Similarly, it follows from the Fourier
cosine integral
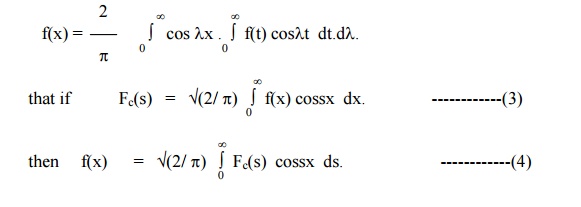
The function Fc(s),
as defined by (3), is known as the Fourier cosine transform of f(x).
Also the function f(x), as given by (4),is called the Inverse Fourier cosine
transform of Fc(s) .
Properties of Fourier sine and cosine
Transforms
If Fs(s) and
Fc(s) are the Fourier sine and cosine transforms of f(x)
respectively, the following properties and identities are true.
(1) Linearity property
Fs
[a f(x) + b g(x) ] = a Fs { f(x) } + b Fs { g(x) }.
and Fc [a f(x) + b g(x) ] = a Fc
{ f(x) } + b Fc { g(x) }.
(2) Change of scale property
Fs
[ f(ax) ] = (1/a) Fs [ s/a ].
and Fc [ f(ax) ] = (1/a) Fc
[ s/a ].
(3) Modulation
Theorem
i.
Fs [ f(x) sinax ] = (1/2) [ Fc
(s-a) - Fc (s+a)].
ii.
Fs [ f(x) cosax ] = (1/2) [ Fs
(s+a) + Fs (s-a)].
iii. Fc[
f(x) cosax ] = (1/2) [ Fc (s+a) + Fc (s-a) ].
iv. Fc[
f(x) sinax ] = (1/2) [ Fs (s+a) - Fs (s-a) ].
Proof
The Fourier sine transform of f(x)sinax
is given by
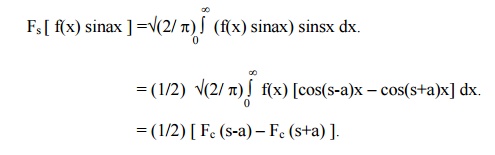
Similarly, we can prove the results (ii), (iii) & (iv).

Similarly, we can prove the second identity and the
other identities follow by setting g(x) = f(x) in the first identity.
Property
(5)
If Fs(s) and Fc(s) are the
Fourier sine and cosine transforms of f(x) respectively, then

Example
8
Find the Fourier sine and cosine
transforms of e-ax and hence deduce the inversion formula.
The Fourier sine transform of f(x) is given by









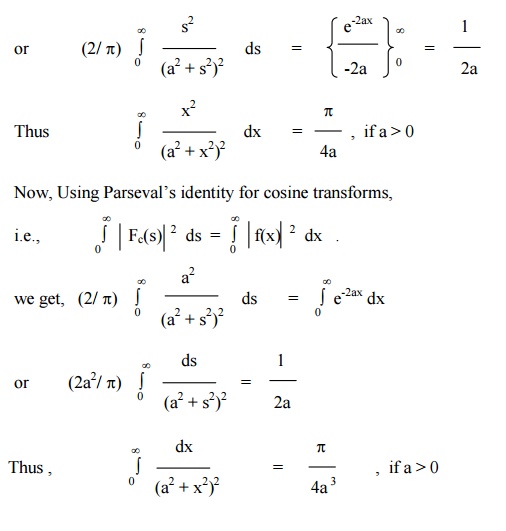
Related Topics