Chapter: Principles of Compiler Design : Syntax Analysis and Run-Time Environments
Writing a Grammar
WRITING
A GRAMMAR
A grammar consists of a number of
productions. Each production has an abstract symbol called a nonterminal
as its left-hand side, and a sequence of one or more nonterminal and terminal
symbols as its right-hand side. For each grammar, the terminal
symbols are drawn from a specified alphabet.
Starting from a sentence consisting of a
single distinguished nonterminal, called the goal symbol, a given
context-free grammar specifies a language, namely, the set of possible
sequences of terminal symbols that can result from repeatedly replacing any
nonterminal in the sequence with a right-hand side of a production for which
the nonterminal is the left-hand side.
REGULAR
EXPRESSION
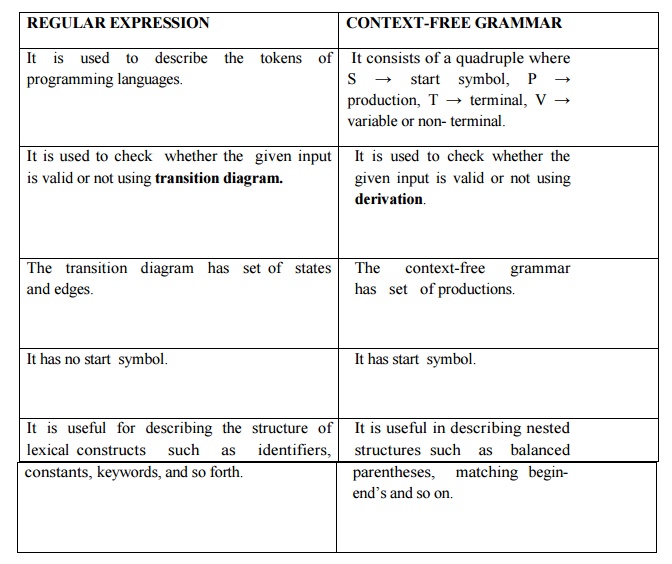
It is used to describe
the tokens of programming languages.
It is used to check
whether the given input is valid or not using transition d
The transition diagram
has set of states and edges.
It has no start symbol.
It is useful for
describing the structure of lexical constructs such asidentifiers,
constants, keywords, and so forth.
CONTEXT-FREE GRAMMAR
It consists of a
quadruple where S → start symbol, P → production, T → terminal, V → variable or
non- terminal.
It is used to check
whether the given input is valid or not using derivation.
The context-free
grammar has set of productions.
It has start symbol.
parentheses, matching
begin- end’s and so on.
There
are four categories in writing a grammar :
1.
Regular Expression Vs Context Free Grammar
2. Eliminating
ambiguous grammar.
3.
Eliminating left-recursion
4.
Left-factoring.
Each parsing method can handle grammars only of a
certain form hence, the initial grammar may have to be rewritten to make it
parsable.
Reasons
for using the regular expression to define the lexical syntax of a language
The lexical rules of a language are simple and RE
is used to describe them.Regular expressions provide a more concise and
easier to understand notation fortokens than grammars.
Ø Efficient
lexical analyzers can be constructed automatically from RE than from grammars.
Ø Separating
the syntactic structure of a language into lexical and nonlexical parts
provides a convenient way of modularizing the front end into two
manageable-sized components.
Eliminating
ambiguity:
Ambiguity of the grammar that produces more than one
parse tree for leftmost or rightmost derivation can be eliminated by re-writing
the grammar.
Consider this example, G: stmt→ifexprthenstmt|ifexprthenstmtelstmte|other
This grammar is ambiguous since the string if E1 then if E2 then S1 else S2
has the following two parse trees for leftmost derivation (Fig. 2.3)
To eliminate ambiguity, the following
grammar may be used: stmt→matched|unmatchedstmt_stmt
matched→ifexprstmtthenmatchedelsematchedtmt_stmt|other
unmatched→ifexprsthenmtstmt|ifexprthenmatchedelseunmatchedtmt_stmt
Eliminating
Left Recursion:
A grammar is said to be left
recursiveifithasanon-terminal Asuch that there is a derivation
A=>Aα for some string α. Top-down parsing methods cannot
handle
left-recursive grammars. Hence, left recursion can be eliminated as follows:
If there is→ aαA produc|βitioncan Abe
replaced with a s A→βA’
A’→αA’
| ε
without
changing the set of strings derivable from A.
Algorithm
to eliminate left recursion: Arrange the
non-terminals in some order A1, A2 . . . An.
1. fori:=
1 tondo begin
forj:=
1 toi-1 do begin replace each
production of the form Ai → Aj
γ by the
productions
Ai → δ1
γ
| δ2γ | . . . | δk γ
where
Aj → δ1 | δ2 | . . . | δk are all
the current Aj-productions;
end
eliminate
the immediate left recursion among the Ai-productions
end

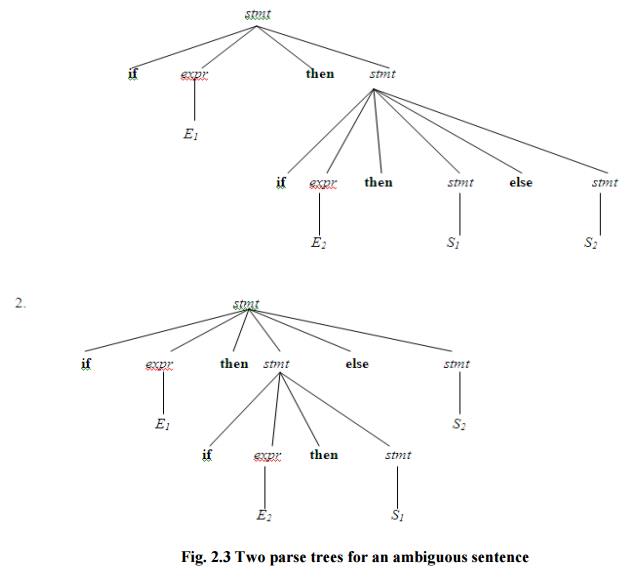
Fig.
2.3 Two parse trees for an ambiguous sentence
Left factoring:
Left
factoring is a grammar transformation that is useful for producing a grammar
suitable for predictive parsing. When it is not clear which of two alternative
productions to use to expand a non-terminal A, we can rewrite the A-productions
to defer the decision until we have seen enough of the input to make the right
choice.
If there is any→αβ1|production2αβ,itcan
beA rewritten as
A→αA’
A’→β1|2 β
Consider the grammar , G : S →
iEtS | iEtSeS | a
E→b
Left factored, this grammar becomes
S → iEtSS’ | a
S’ → eS |ε E → b
Related Topics