Chapter: Principles of Compiler Design : Syntax Analysis and Run-Time Environments

Context-Free Grammars

A Context-Free Grammar is a quadruple that consists of terminals,non-terminals, start symbol and productions.

CONTEXT-FREE GRAMMARS

A Context-Free Grammar is a quadruple that consists of terminals,non-terminals, start symbol and productions.

Terminals: These are the basic symbols from which strings are formed.

Non-Terminals: These are the syntactic variables that denote a set of strings.

These help to define the language generated by the grammar.

Start Symbol: Onenon-terminal in the grammar is denoted as the “Start-symbol” and the setof strings it denotes is the language defined by the grammar.

Productions : It specifies the manner in which terminals and non-terminals can be combinedto form strings. Each production consists of a non-terminal, followed by an arrow, followed by a string of non-terminals and terminals.

Example of context-free grammar:

The following grammar defines simple arithmetic expressions

: expr → expr op expr expr → (expr)

expr → - expr

expr → id

op → +

op → -

op → *

op → /

op → ↑

In this grammar,

v id + - * / ↑ ( ) are terminals.

expr , op are non-terminals.

expr is the start symbol.

Each line is a production.

Derivations:

Two basic requirements for a grammar are :

1. To generate a valid string.

2. To recognize a valid string.

Derivation is a process that generates a valid string with the help of grammar by replacing the non-terminals on the left with the string on the right side of the production.

Example : Consider the following grammar for arithmetic expressions :

E→E+E|E*E|(E)|-E| id

To generate a valid string - ( id+id ) from the grammar the steps are

1. E → - E

2. E → - ( E )

3. E → - ( E+E )

4. E → - ( id+E )

5. E → - ( id+id )

In the above derivation,

E is the start symbol

-(id+id) is therequiredsentence(only terminals).

Strings such as E, -E, -(E), . . . are called sentinel forms.

Types of derivations:

The two types of derivation are:

1. Left most derivation

2. Right most derivation.

 In leftmost derivations, the leftmost non-terminal in each sentinel is always chosen first for replacement.

In rightmost derivations, the rightmost non-terminal in each sentinel is always chosen first for replacement.

Example:

Given grammar G : E → E+E | E*E | ( E ) | - E | id Sentence to be derived : - (id+id)

Left Most Derivation

E→-E

E→-(E)

E→-(E+E)

E→-(id+E)

E→-(id+id)

Right Most Derivation

E→-E

E→-(E)

E→-(E+E)

E→-(E+id)

E→-(id+id)

String that appear in leftmost derivation are called left sentinel forms.

String that appear in rightmost derivation are called right sentinel forms.

Sentinels:

Given a grammar G with start symbol S, if S → α , where α may contain non-terminals or terminals, then α is called the sentinel form of G.

Yield or frontier of tree:

Each interior node of a parse tree is a non-terminal. The children of node can be a terminal or non-terminal of the sentinel forms that are read from left to right. The sentinel form in the parse tree is called yield or frontier of the tree.

Ambiguity:

A grammar that produces more than one parse for some sentence is said to be ambiguous

grammar.

Example : Given grammar G : E → E+E | E*E | ( E ) | - E | id

The sentence id+id*id has the following two distinct leftmost derivations:

E → E+ E

E → E* E

E → id + E

E→E+ E * E

E → id + E * E

E → id + id * E

E → id + id * id

The two corresponding trees are,

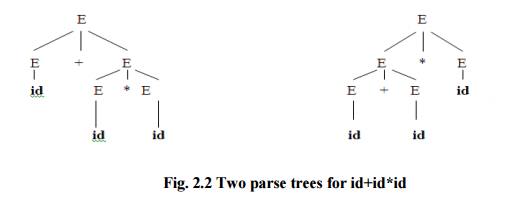
Fig. 2.2 Two parse trees for id+id*id

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

Principles of Compiler Design : Syntax Analysis and Run-Time Environments : Context-Free Grammars |