Top down parsing and Bottom up Parsing

PARSING

It is the process of analyzing a continuous stream of input in order to determine its grammatical structure with respect to a given formal grammar.

Parse tree:

Graphical representation of a derivation or deduction is called a parse tree. Each interior node of the parse tree is a non-terminal; the children of the node can be terminals or non-terminals.

Types of parsing:

1.     Top down parsing

2.     Bottom up parsing

Ø    Top-down parsing : A parser can start with the start symbol and try to transform it to the input string. Example : LL Parsers.

Ø     Bottom-up parsing : A parser can start with input and attempt to rewrite it

into the start symbol. Example : LR Parsers.

TOP-DOWN PARSING

It can be viewed as an attempt to find a left-most derivation for an input string or an attempt to construct a parse tree for the input starting from the root to the leaves.

Types -downoftopparsing :

1.   Recursive descent parsing

2.   Predictive parsing

RECURSIVE DESCENT PARSING

Typically, top-down parsers are implemented as a set of recursive functions that descent through a parse tree for a string. This approach is known as recursive descent parsing, also known as LL(k) parsing where the first L stands for left-to-right, the second L stands for leftmost-derivation, and k indicates k-symbol lookahead.

Therefore, a parser using the single-symbol look-ahead method and top-down parsing without backtracking is called LL(1) parser. In the following sections, we will also use an extended BNF notation in which some regulation expression operators are to be incorporated.

This parsing method may involve backtracking.

Example for :backtracking

Consider the grammar G : S → cAd

A→ab|a

and the input string w=cad.

The parse tree can be constructed using the following top-down approach :

Step1:

Initially create a tree with single node labeled S. An input pointer points to ‘c’, the first symbol of w. Expand the tree with the production of S.

Step2:

The leftmost leaf ‘c’ matches the first symbol of w, so advance the input pointer to the second symbol of w ‘a’ and consider the next leaf ‘A’. Expand A using the first alternative.

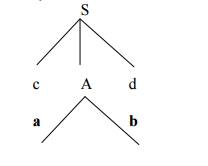
Step3:

The second symbol ‘a’ of w also matches with second leaf of tree. So advance the input pointer to third symbol of w ‘d’.But the third leaf of tree is b which does not match with the input symbol d.Hence discard the chosen production and reset the pointer to second backtracking.

Step4:

Now try the second alternative for A.

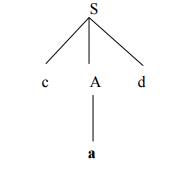
Now we can halt and announce the successful completion of parsing.

Predictive parsing

It is possible to build a nonrecursive predictive parser by maintaining a stack explicitly, rather than implicitly via recursive calls. The key problem during predictive parsing is that of determining the production to be applied for a nonterminal . The nonrecursive parser in figure looks up the production to be applied in parsing table. In what follows, we shall see how the table can be constructed directly from certain grammars.

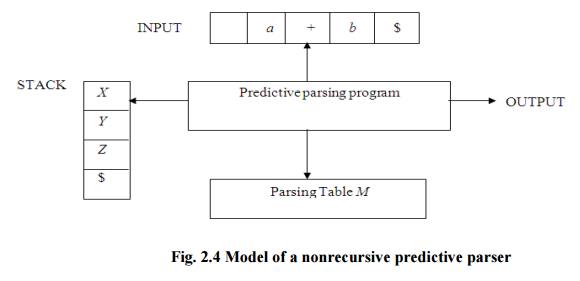
Fig. 2.4 Model of a nonrecursive predictive parser

A table-driven predictive parser has an input buffer, a stack, a parsing table, and an output stream. The input buffer contains the string to be parsed, followed by $, a symbol used as a right endmarker to indicate the end of the input string. The stack contains a sequence of grammar symbols with $ on the bottom, indicating the bottom of the stack. Initially, the stack contains the start symbol of the grammar on top of $. The parsing table is a two dimensional array M[A,a] where A is a nonterminal, and a is a terminal or the symbol $. The parser is controlled by a program that behaves as follows. The program considers X, the symbol on the top of the stack, and a, the current input symbol. These two symbols determine the action of the parser. There are three possibilities.

1 If X= a=$, the parser halts and announces successful completion of parsing.

2   If X=a!=$, the parser pops X off the stack and advances the input pointer to the next input symbol.

3   If X is a nonterminal, the program consults entry M[X,a] of the parsing table M. This entry will be either an X-production of the grammar or an error entry. If, for example, M[X,a]={X- >UVW}, the parser replaces X on top of the stack by WVU( with U on top). As output, we shall assume that the parser just prints the production used; any other code could be executed here. If M[X,a]=error, the parser calls an error recovery routine

Algorithm for Nonrecursive predictive arsing.

Input. A string w and a parsing table M for grammar G.

Output. If w is in L(G), a leftmost derivation of w; otherwise, an error indication.

Method. Initially, the parser is in a configuration in which it has $S on the stack with S, the start symbol of G on top, and w$ in the input buffer. The program that utilizes the predictive parsing table M to produce a parse for the input is shown in Fig.

set ip to point to the first symbol of w$. repeat

let X be the top stack symbol and a the symbol pointed to by ip. if X is a terminal of $ then

if X=a then

pop X from the stack and advance ip else error()

else

if M[X,a]=X->Y1Y2...Yk then begin pop X from the stack;

push Yk,Yk-1...Y1 onto the stack, with Y1 on top; output the production X-> Y1Y2...Yk

end

else error()

until X=$ /* stack is empty */

Predictive parsing table construction:

The construction of a predictive parser is aided by two functions associated with a grammar G :

3. FIRST

4. FOLLOW

Rules for first( ):

1. If X is terminal, then FIRST(X) is {X}.

2. If X → ε is a production, then add ε to FIRST(X).

3. If X is non-terminal and X → aα is a production then add a to FIRST(X).

4. If X is non-terminal and X → Y1 Y2…Yk is a production, then place a in FIRST(X) if for some i, a is in FIRST(Yi), and ε is in all of FIRST(Y1),…,FIRST(Yi-1);that is, Y1,….Yi-1=> ε. If ε is in FIRST(Yj) for all j=1,2,..,k, then add ε to FIRST(X).

Rules for follow( ):

1. If S is a start symbol, then FOLLOW(S) contains $.

2. If there is a production A → αBβ, then everything in FIRST(β) except ε is placed in

follow(B).

3. If there is a production A → αB, or a production A → αBβ where FIRST(β) contains

ε, then everything in FOLLOW(A) is in FOLLOW(B).

Algorithm for construction of predictive parsing table:

Input : Grammar G

Output : Parsing table M

Method :

1. For each production A → α of the grammar, do steps 2 and 3.

2. For each terminal a in FIRST(α), add A → α to M[A, a].

3. If ε is in FIRST(α), add A → α to M[A, b] for each terminal b in FOLLOW(A). If ε is in FIRST(α) and $ is in FOLLOW(A) , add A → α to M[A, $].

4. Make each undefined entry of M be error.

Example:

Consider the following grammar :

E→E+T|T

T→T*F|F

F→(E)|id

After eliminating left-recursion the grammar is

E →TE’

E’ → +TE’ | ε

T →FT’

T’ → *FT’ | ε

F → (E)|id

First( ) :

FIRST(E) = { ( , id}

FIRST(E’) ={+ , ε }

FIRST(T) = { ( , id}

FIRST(T’) = {*, ε }

FIRST(F) = { ( , id }

Follow( ):

FOLLOW(E) = { $, ) }

FOLLOW(E’) = { $, ) }

FOLLOW(T) = { +, $, ) }

FOLLOW(T’) = { +, $, ) }

FOLLOW(F) = {+, * , $ , ) }

Predictive parsing Table

Stack Implementation

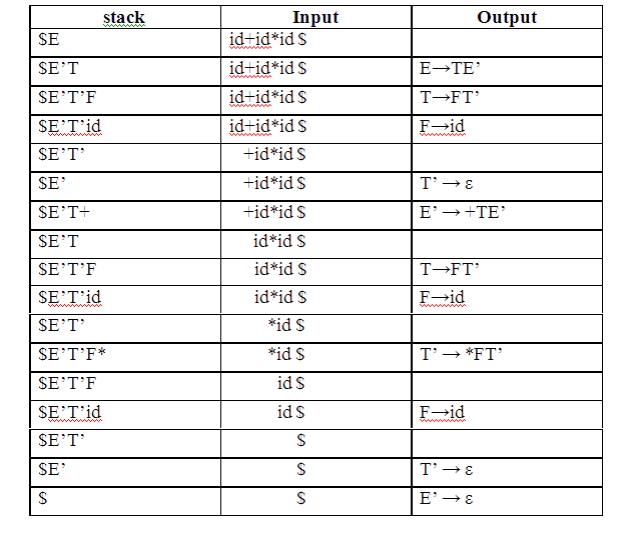
LL(1) grammar:

The parsing table entries are single entries. So each location has not more than one entry. This type of grammar is called LL(1) grammar.

Consider this following grammar:

S→iEtS | iEtSeS| a

E→b

After eliminating left factoring, we have

S→iEtSS’|a

S’→ eS | ε

E→b

To construct a parsing table, we need FIRST() and FOLLOW() for all the non-terminals.

FIRST(S) = { i, a }

FIRST(S’) = {e, ε }

FIRST(E) = { b}

FOLLOW(S) = { $ ,e }

FOLLOW(S’) = { $ ,e }

FOLLOW(E) = {t}

Parsing table:

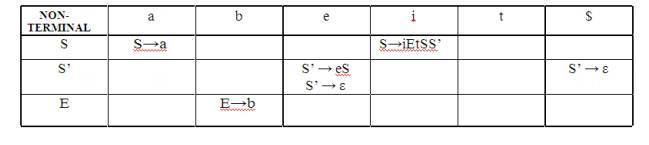
Since there are more than one production, the grammar is not LL(1) grammar.

Actions performed in predictive parsing:

1.  Shift

2.  Reduce

3.   Accept

4.   Error

Implementation of predictive parser:

1.   Elimination of left recursion, left factoring and ambiguous grammar.

2.  Construct FIRST() and FOLLOW() for all non-terminals.

3.  Construct predictive parsing table.

4.  Parse the given input string using stack and parsing table

BOTTOM-UP PARSING

Constructing a parse tree for an input string beginning at the leaves and going towards the root is called bottom-up parsing. A general type of bottom-up parser is a shift-reduce parser.

SHIFT-REDUCE PARSING

Shift-reduce parsing is a type of bottom-up parsing that attempts to construct a parse tree for an input string beginning at the leaves (the bottom) and working up towards the root (the top).

Example:

Consider the grammar:

S → aABe

A → Abc | b

B → d

The sentence to be recognized is abbcde.

REDUCTION (LEFTMOST)         RIGHTMOST DERIVATION

abbcde (A → b)    S → aABe 

aAbcde(A → Abc)         → aAde     

aAde (B → d)      → aAbcde  

aABe (S → aABe)          → abbcde  

S

The reductions trace out the right-most derivation in reverse.

Handles:

A handle of a string is a substring that matches the right side of a production, and whose reduction to the non-terminal on the left side of the production represents one step along the reverse of a rightmost derivation.

Example:

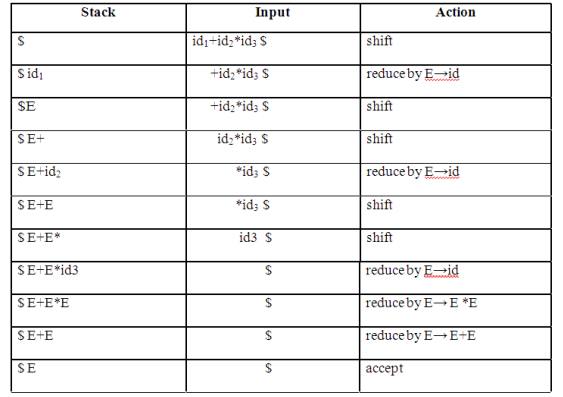
Consider the grammar:

E→E+E

E→E*E

E→(E)

E→id

And the input string id1+id2*id3

The rightmost derivation is :

E→E+E

→ E+E*E

→ E+E*id3

→ E+id2*id3

→ id1+id2*

In the above derivation the underlined substrings are called handles.

Handle pruning:

A rightmost derivation in reverse can be obtained by “handle pruning”. (i.e.) if w is a sentence or string of the grammar at hand, then w = γn, where γn is the nth rightsentinel form of

some rightmost derivation.

Actions in shift-reduce parser:

•   shift - The next input symbol is shifted onto the top of the stack.

•   reduce - The parser replaces the handle within a stack with a non-terminal.

•   accept - The parser announces successful completion of parsing.

•   error - The parser discovers that a syntax error has occurred and calls an error recovery routine.

Conflicts in shift-reduce parsing:

There are two conflicts that occur in shift-reduce parsing:

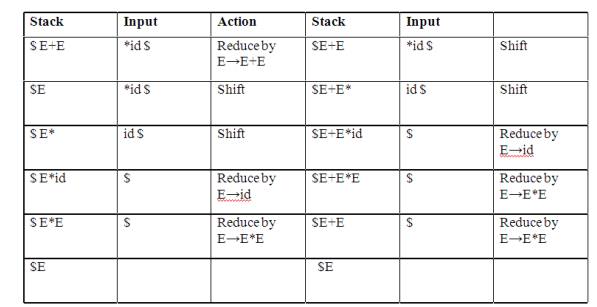
1. Shift-reduce conflict: The parser cannot decide whether to shift or to reduce.

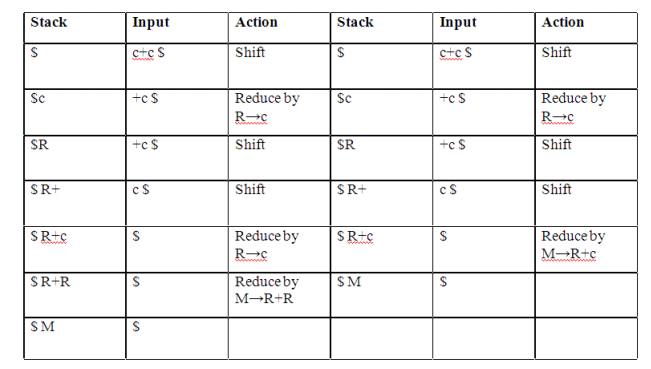
2. Reduce-reduce conflict: The parser cannot decide which of several reductions to make.

Stack implementation of shift-reduce parsing :

1. Shift-reduce conflict: 

Example:

Consider the grammar:

E→E+E | E*E | id and input id+id*id

2. Reduce-reduce conflict:

Consider the grammar: M→R+R|R+c|R

R→c

and input c+c

Viable prefixes:

α is a viable prefix of the grammar if there is w such that αw is a right

The set of prefixes of right sentinel forms that can appear on the stack of a shift-reduce parser are called viable prefixes

The set of viable prefixes is a regular language.

OPERATOR-PRECEDENCE PARSING

An efficient way of constructing shift-reduce parser is called operator-precedence parsing. Operator precedence parser can be constructed from a grammar called Operator-grammar. These grammars have the property that no production on right side is ɛor has two adjacent non-terminals.

Example:

Consider the grammar:

E→EAE|(E)|-E|id

A→+|-|*|/|↑

Since the right side EAE has three consecutive non-terminals, the grammar can be written as follows: E→E+E|E-E|E*E|E/E|E↑E |-E|id

Operator precedence relations:

There are three disjoint precedence relations namely

<. - less than

=                   - equal to

.> - greater than

The relations give the following meaning:

a<.b - a yields precedence to b

a=b - a has the same precedence as b

a.>b - a takes precedence over b

Rules for binary operations:

1. If operator θ1 has higher precedence than operator θ2, then make

θ1 . > θ2 and θ2 < . θ1

2. If operators θ1 and θ2, are of equal precedence, then make

θ1 . > θ2 and θ2 . > θ1 if operators are left associative

θ1 < . θ2 and θ2 < . θ1 if right associative

3. Make the following for all operators θ:

θ  <. id ,id.>θ

θ  <.(, (<.θ

).>θ, θ.>)

θ.>$ , $<. θ

Also make

( = ) , ( <. ( , ) .> ) , (<. id, id .>) , $ <. id , id .> $ , $ Example:

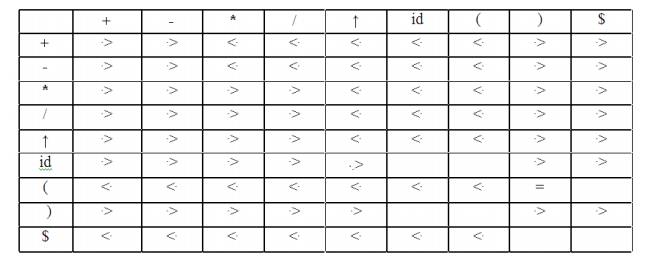
Operator-precedence relations for the grammar

E→E+E|E-E|E*E|E/E|E↑E |(E)|-E|idis given in the following table assuming

1.                 ↑ is of highest precedence and right-associative

2.                 * and / are of next higher precedence and left-associative, and

3.                 + and - are of lowest precedence and left- Note that the blanks in the table denote error entries.

Table : Operator-precedence relations

Operator precedence parsing algorithm:

Input : An input string w and a table of precedence relations.

Output : If w is well formed, a skeletal parse tree ,with a placeholder non-terminal E labeling all interior nodes; otherwise, an error indication.

Method : Initially the stack contains $ and the input buffer the string w $. To parse, we execute the following program :

(1) Set ip to point to the first symbol of w$;

(2)             repeat forever

(3) if $ is on top of the stack and ip points to $ then

(4)             return else begin

(5)             let a be the topmost terminal symbol on the stack and let b be the symbol pointed to by ip;

(6)             if a <. b or a = b then begin

(7)             push b onto the stack;

(8)             advance ip to the next input symbol; end;

(9) else if a . > b then /*reduce*/

(10)        repeat

(11)        pop the stack

(12)        until the top stack terminal is related by <.to the terminal most recently popped

(13)        else error( ) end

Stack implementation of operator precedence parsing:

Operator precedence parsing uses a stack and precedence relation table for its implementation of above algorithm. It is a shift-reduce parsing containing all four actions shift, reduce, accept and error.

The initial configuration of an operator precedence parsing is

STACK : $

INPUT : w$

where w is the input string to be parsed.

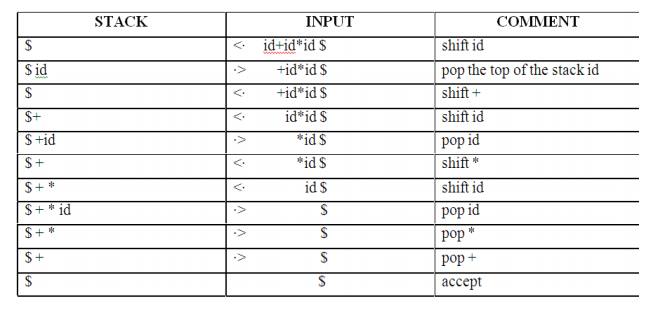
Example:

Consider the grammar E → E+E | E-E | E*E | E/E | E↑E | (E) | id. Input string is id+id*id .The implementation is as follows:

Advantages of operator precedence parsing:

1.   It is easy to implement.

2.    Once an operator precedence relation is made between all pairs of terminals of a grammar, the grammar can be ignored. The grammar is not referred anymore during implementation.

Disadvantages of operator precedence parsing:

1.   It is hard to handle tokens like the minus sign (-) which has two different precedence.

2.   Only a small class of grammar can be parsed using operator-precedence parser.

LR PARSERS

An efficient bottom-up syntax analysis technique that can be used CFG is called LR(k) parsing. The ‘L’ is for left-to-right scanning of the input, the ‘R’ for constructing a rightmost derivation in reverse, and the ‘k’ for the number of input symbols. When ‘k’ is omitted, it is

assumed to be 1.

Advantages of LR parsing:

1. It recognizes virtually all programming language constructs for which CFG can be written.

2.     It is an efficient non-backtracking shift-reduce parsing method.

3.     A grammar that can be parsed using LR method is a proper superset of a grammar that can be parsed with predictive parser

4.     4. It detects a syntactic error as soon as possible.

Drawbacks of LR method:

It is too much of work to construct a LR parser by hand for a programming language grammar. A specialized tool, called a LR parser generator, is needed. Example: YACC.

Types of LR parsing method:

1. SLR- Simple LR

Easiest to implement, least powerful.

2. CLR- Canonical LR

Most powerful, most expensive.

3. LALR- Look-Ahead LR

Intermediate in size and cost between the other two methods.

The LR parsing algorithm:

The schematic form of an LR parser is as follows:

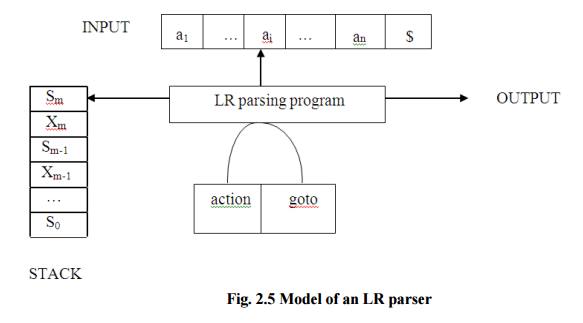
Fig. 2.5 Model of an LR parser

It consists of an input, an output, a stack, a driver program, and a pa parts (action and goto).

Ø     The driver program is the same for all LR parser.

Ø     The parsing program reads characters from an input buffer one at a time.

Ø     The program uses a stack to store a string of the form s0X1s1X2s2…Xmsm, where sm is on top. Each Xi is a grammar symbol and each si is a state.

Ø     The parsing table consists of two parts : action and goto functions.

Action : The parsing program determines sm, the state currently on top of stack, and ai, the current input symbol. It then consults action[sm,ai] in the action table which can have one of four values:

1. shift s, where s is a state,

2. reduce by a grammar production A → β,

3. accept,

4. 4. error.

Goto : The function goto takes a state and grammar symbol as arguments and produces a state.

LR Parsing algorithm:

Input: An input string w and an LR parsing table with functions action and goto for grammar G. Output: If w is in L(G), a bottom-up-parse for w; otherwise, an error indication.

Method: Initially, the parser has s0 on its stack, where s0 is the initial state, and w$ in the input buffer. The parser then executes the following program:

set ip to point to the first input symbol of w$; repeat forever begin

let s be the state on top of the stack and

a the symbol pointed to by ip;

 if action[s, a] = shift s’ then begin

push a then s’ on top of the stack; advance ip to the next input symbol end

else if action[s, a] = reduce A→β then begin pop 2* | β | symbols off the stack;

let s’ be the state now on top of the stack; push A then goto[s’, A] on top of the stack; output the production A→ β

end

else if action[s, a] = accept then

return

else error( )

end