Viscosity of a Liquid By Stoke’s Method

VISCOSITY OF A LIQUID BY STOKE’S METHOD

AIM

To determine the co-efficient of viscosity of the given liquid by stoke’s method

APPARATUS REQUIRED

A long cylindrical glass jar, highly viscous liquid, metre scale, spherical ball, stop clock, thread.

FORMULA

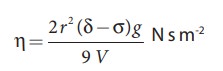
Where

 Î· - Coefficient of viscosity of liquid (N s m^–2)

r → radius of spherical ball ( m )

δ→ density of the steel sphere ( kg m^–3 )

σ→ density of the liquid ( kg m^–3 )

g → acceleration due to gravity (9.8 m s^–2 )

V → mean terminal velocity ( m s^–1 )

DIAGRAM

PROCEDURE

·         A long cylindrical glass jar with markings is taken.

·         Fill the glass jar with the given experimental liquid.

·         Two points A and B are marked on the jar. The mark A is made well below the surface of the liquid so that when the ball reaches A it would have acquired terminal velocity V.

·         The radius of the metal spherical ball is determined using screw gauge.

·         The spherical ball is dropped gently into the liquid.

·         Start the stop clock when the ball crosses the point A. Stop the clock when the ball reaches B.

·         Note the distance between A and B and use it to calculate terminal velocity.

·         Now repeat the experiment for different distances between A and B. Make sure that the point A is below the terminal stage.

OBSERVATIONS

To find Terminal Velocity:

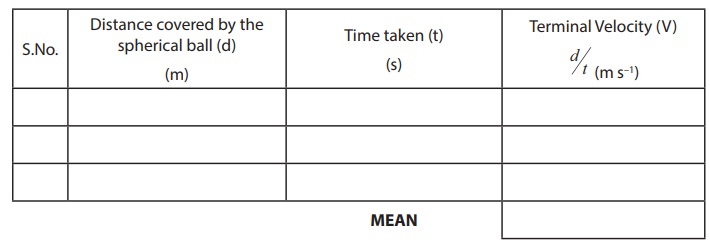
CALCULATION

Density of the spherical ball δ = ________ kg m^−3

Density of the given liquid σ = ________ kg m^−3

Coefficient of viscosity of the liquid η = 2r²g(δ −σ) / 9V  =  = ________ N s m^–2

RESULT

The coefficient of viscosity of the given liquid by stoke’s method η = ________ Nsm^–2