Spring Constant of a Spring

SPRING CONSTANT OF A SPRING

AIM

To determine the spring constant of a spring by using the method of vertical oscillations

APPARATUS REQUIRED

Spring, rigid support, hook, 50 g mass hanger, 50 g slotted masses, stop clock, metre scale, pointer

FORMULA

Spring constant of the spring k

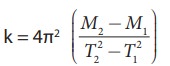
where

M₁, M₂ → selected loads in kg

T₁, T₂ → time period corresponding to masses M₁ and M₂ respectively in second

DIAGRAM

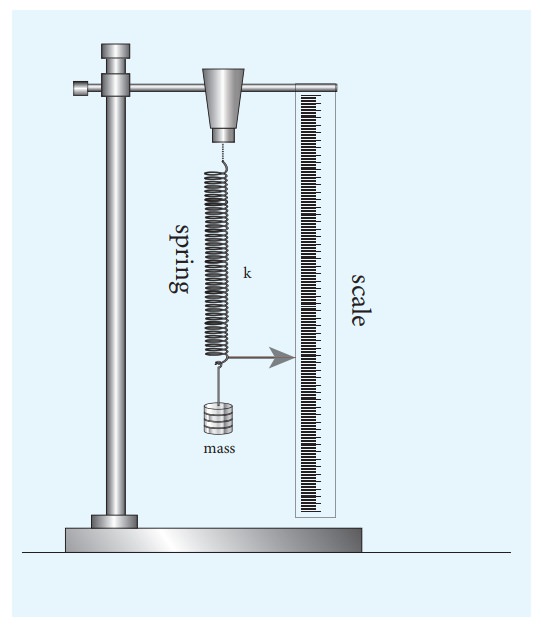
PROCEDURE

·           A spring is firmly suspended vertically from a rigid clamp of a wooden stand at its upper end with a mass hanger attached to its lower end. A pointer fixed at the lower end of the spring moves over a vertical scale fixed.

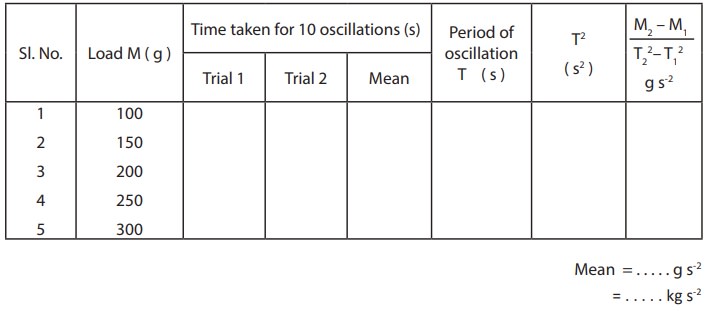
·         A suitable load M (eg; 100 g ) is added to the mass hanger and the reading on the scale at which the pointer comes to rest is noted. This is the equilibrium position.

·         The mass in the hanger is pulled downward and released so that the spring oscillates vertically on either side of the equilibrium position.

·         When the pointer crosses the equilibrium position a stop clock is started and the time taken for 10 vertical oscillations is noted. Then the period of oscillation T is calculated.

·         The experiment is repeated by adding masses in steps of 50 g to the mass hanger and period of oscillation at each time is calculated.

·         For the masses M₁ and M₂ ( with a difference of 50 g ), if T₁ and T₂ are the corresponding periods, then the value M₂ – M₁ / T₂² – T₁² is calculated and its average is found.

·         Using the given formula the spring constant of the given spring is calculated.

OBSERVATIONS

CALCULATION

Spring constant of the spring k

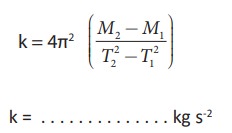
RESULT

The spring constant of the given spring k = . . . . . . . . . . . . kg s^-2