Non - Uniform Bending - Verification of Relation Between Load and Depression Using Pin and Microscope

NON – UNIFORM BENDING – VERIFICATION OF RELATION BETWEEN LOAD AND DEPRESSION USING PIN AND MICROSCOPE

AIM

To verify the relation between the load and depression using non-uniform bending of a beam.

APPARATUS REQUIRED

A long uniform beam (usually a metre scale), two knife – edge supports, mass hanger, slotted masses, pin, vernier microscope

FORMULA

M/s = a constant

where

M → Load applied (mass) (kg)

s → depression for the applied load(metre)

DIAGRAM

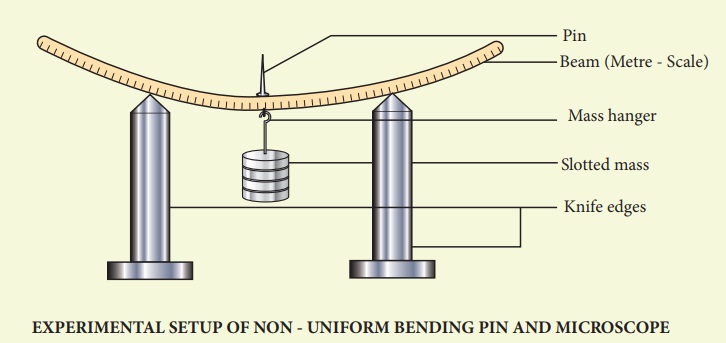
PROCEDURE

·           Place the two knife – edges on the table.

·           Place the uniform beam (metre scale) on top of the knife edges.

·           Suspend the mass hanger at the centre. A pin is attached at the centre of the scale where the hanger is hung.

·           Place a vernier microscope in front of this arrangement

·           Adjust the microscope to get a clear view of the pin

·         Make the horizontal cross-wire on the microscope to coincide with the tip of the pin. (Here mass hanger is the dead load M).

·         Note the vertical scale reading of the vernier microscope

·         Add the slotted masses one by one in steps of 0.05 kg (50 g) and take down the readings.

·         Then start unloading by removing masses one by one and note the readings.

·           Subtract the mean reading of each load from dead load reading. This gives the depressions for the corresponding load M.

OBSERVATIONS

To find M/s

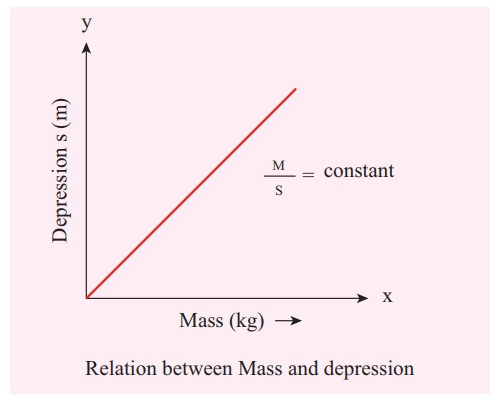
MODEL GRAPH

Load (M) vs Depression (s)

A graph between M and s can be drawn by taking M along X- axis and s along Y – axis.

This is a straight line.

CALCULATION

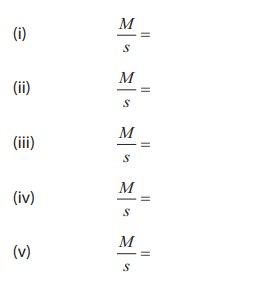
RESULT

·         The ratio between mass and depression for each load is calculated. This is found to be constant.

·           Thus the relation between load and depression is verified by the method of non-uniform bending of a beam.