Variants of Syntax Trees

Variants of Syntax Trees

1 Directed Acyclic Graphs for Expressions

2 The Value-Number Method for Constructing DAG's

3 Exercises for Section 6.1

Nodes in a syntax tree represent constructs in the source program; the children of a node represent the meaningful components of a construct. A directed acyclic graph (hereafter called a DAG) for an expression identifies the common subexpressions (subexpressions that occur more than once) of the expression. As we shall see in this section, DAG's can be constructed by using the same techniques that construct syntax trees.

1. Directed Acyclic Graphs for Expressions

Like the syntax tree for an expression, a DAG has leaves corresponding to atomic operands and interior codes corresponding to operators. The difference is that a node N in a DAG has more than one parent if N represents a com-mon subexpression; in a syntax tree, the tree for the common subexpression would be replicated as many times as the subexpression appears in the original expression. Thus, a DAG not only represents expressions more succinctly, it gives the compiler important clues regarding the generation of efficient code to evaluate the expressions.

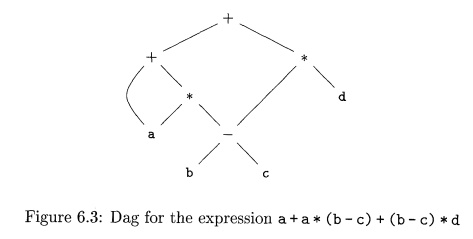
Example 6.1:  Figure 6.3 shows the DAG for the expression

a +  a  *         (b  -  c)   +   (b  -  c)        *  d

The leaf for a has two parents, because a appears twice in the expression. More interestingly, the two occurrences of the common subexpression b - c are represented by one node, the node labeled —. That node has two parents, representing its two uses in the subexpressions a* (b - c) and (b - c)*d . Even though b and c appear twice in the complete expression, their nodes each have one parent, since both uses are in the common subexpression b - c . •

The SDD of Fig. 6.4 can construct either syntax trees or DAG's. It was used to construct syntax trees in Example 5.11, where functions Leaf and Node created a fresh node each time they were called. It will construct a DAG if, before creating a new node, these functions first check whether an identical node already exists. If a previously created identical node exists, the existing node is returned. For instance, before constructing a new node, Node(op, left, right) we check whether there is already a node with label op, and children left and right, in that order. If so, Node returns the existing node; otherwise, it creates a new node.

Example 6.2 : The sequence of steps shown in Fig. 6.5 constructs the DAG in Fig. 6.3, provided Node and Leaf return an existing node, if possible, as discussed abve. We assume that entry-a points to the symbol-table entry for a, and similarly for the other identifiers.

When the call to Leaf (id, entry-a) is repeated at step 2, the node created by the previous call is returned, so p2 = Pi • Similarly, the nodes returned at steps 8 and 9 are the same as those returned at steps 3 and 4 (i.e., ps = p3 and PQ = p^). Hence the node returned at step 10 must be the same at that returned at step 5; i.e., pio = P5- •

2. The Value-Number Method for Constructing DAG's

Often, the nodes of a syntax tree or DAG are stored in an array of records, as suggested by Fig. 6.6. Each row of the array represents one record, and therefore one node. In each record, the first field is an operation code, indicating the label of the node. In Fig. 6.6(b), leaves have one additional field, which holds the lexical value (either a symbol-table pointer or a constant, in this case), and interior nodes have two additional fields indicating the left and right children.

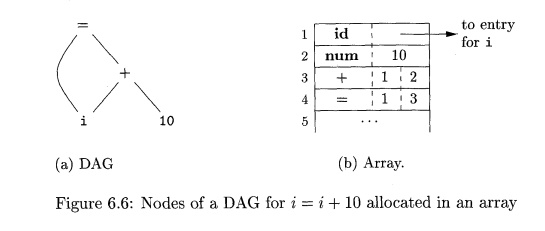
In this array, we refer to nodes by giving the integer index of the record for that node within the array. This integer historically has been called the value number for the node or for the expression represented by the node. For instance, in Fig. 6.6, the node labeled -I- has value number 3, and its left and right children have value numbers 1 and 2, respectively. In practice, we could use pointers to records or references to objects instead of integer indexes, but we shall still refer to the reference to a node as its "value number." If stored in an appropriate data structure, value numbers help us construct expression DAG's efficiently; the next algorithm shows how.

Suppose that nodes are stored in an array, as in Fig. 6.6, and each node is referred to by its value number. Let the signature of an interior node be the triple (op,/,r), where op is the label, I its left child's value number, and r its right child's value number. A unary operator may be assumed to have r = 0-

Algorithm 6.3 The value-number method for constructing the nodes of a DAG.

INPUT : Label op, node /, and node r.

OUTPUT : The value number of a node in the array with signature (op, l,r).

METHOD : Search the array for a node M with label op, left child I, and right child r. If there is such a node, return the value number of M. If not, create in the array a new node N with label op, left child I, and right child r, and return its value number.

While Algorithm 6.3 yields the desired output, searching the entire array every time we are asked to locate one node is expensive, especially if the array holds expressions from an entire program. A more efficient approach is to use a hash table, in which the nodes are put into "buckets," each of which typically will have only a few nodes. The hash table is one of several data structures that support dictionaries efficiently.¹ A dictionary is an abstract data type that allows us to insert and delete elements of a set, and to determine whether a given element is currently in the set. A good data structure for dictionaries, such as a hash table, performs each of these operations in time that is constant or close to constant, independent of the size of the set.

To construct a hash table for the nodes of a DAG, we need a hash function h that computes the index of the bucket for a signature (op, I, r), in a way that distributes the signatures across buckets, so that it is unlikely that any one bucket will get much more than a fair share of the nodes. The bucket index h(op, I, r) is computed deterministically from op, I, and r, so that we may repeat the calculation and always get to the same bucket index for node (op, I, r).

The buckets can be implemented as linked lists, as in Fig. 6.7. An array, indexed by hash value, holds the bucket headers, each of which points to the first cell of a list. Within the linked list for a bucket, each cell holds the value number of one of the nodes that hash to that  bucket. That is,  node  (op,l,r) can be found on the list whose header is at index h(op,l,r)  of the array.

Thus, given the input node op, I, and r, we compute the bucket index h(op,l,r) and search the list of cells in this bucket for the given input node. Typically, there are enough buckets so that no list has more than a few cells. We may need to look at all the cells within a bucket, however, and for each value number v found in a cell, we must check whether the signature (op,l,r) of the input node matches the node with value number v in the list of cells (as in Fig. 6.7) . If we find a match, we return v. If we find no match, we know no such node can exist in any other bucket, so we create a new cell, add it to the list of cells for bucket index h(op, l,r), and return the value number in that new cell.

3. Exercises for Section 6.1

Exerc ise 6. 1 . 1 :  Construct the DAG for the expression

((a;  + y)-  {{x  + y)*(x- y)))  +  ((x + y)  *  (x  - y))

Exercise 6 . 1 . 2 : Construct the DAG and identify the value numbers for the subexpressions of the following expressions, assuming + associates from the left.

     a + b+ (a + b).

     a + b + a + b.

    a + a + ((fl + a + a + (a + a + a + a)) .