Control Flow

Control Flow

1 Boolean Expressions

 2 Short-Circuit Code

 3 Flow-of-Control Statements

 4 Control-Flow Translation of Boolean Expressions

 5 Avoiding Redundant Gotos

 6 Boolean Values and Jumping Code

 7 Exercises for Section 6.6

The translation of statements such as if-else-statements and while-statements is tied to the translation of boolean expressions. In programming languages, boolean expressions are often used to

1. Alter the flow of control. Boolean expressions are used as conditional expressions in statements that alter the flow of control. The value of such boolean expressions is implicit in a position reached in a program. For example, in if (E) 5, the expression E must be true if statement S is reached.

2. Compute logical values. A boolean expression can represent true Or false as values. Such boolean expressions can be evaluated in analogy to arith-metic expressions using three-address instructions with logical operators.

The intended use of boolean expressions is determined by its syntactic context. For example, an expression following the keyword if is used to alter the flow of control, while an expression on the right side of an assignment is used to denote a logical value. Such syntactic contexts can be specified in a number of ways: we may use two different nonterminals, use inherited attributes, or set a flag during parsing. Alternatively we may build a syntax tree and invoke different procedures for the two different uses of boolean expressions.

This section concentrates on the use of boolean expressions to alter the flow of control. For clarity, we introduce a new nonterminal B for this purpose. In Section 6.6.6, we consider how a compiler can allow boolean expressions to represent logical values.

1.  Boolean Expressions

Boolean expressions are composed of the boolean operators (which we denote &&, I I, and !, using the C convention for the operators AND, OR, and NOT, respectively) applied to elements that are boolean variables or relational ex-pressions. Relational expressions are of the form E_± rel E₂, where Ex and E₂ are arithmetic expressions. In this section, we consider boolean expressions generated by the following grammar:

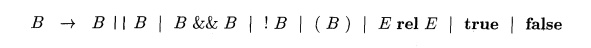
We use the attribute rel. op to indicate which of the six comparison operators <, < = , =, ! =, >, or >= is represented by rel. As is customary, we assume that I I and &;& are left-associative, and that I I has lowest precedence, then &&, then !.

 Given the expression Bi I I B2, if we determine that B1 is true, then we can conclude that the entire expression is true without having to evaluate B2.

Similarly, given B1k,kB2, if Bi is false, then the entire expression is false. The semantic definition of the programming language determines whether all parts of a boolean expression must be evaluated. If the language definition permits (or requires) portions of a boolean expression to go unevaluated, then the compiler can optimize the evaluation of boolean expressions by computing only enough of an expression to determine its value. Thus, in an expression such as B1 I I B2, neither B1 nor B2 is necessarily evaluated fully. If either B1 or B2 is an expression with side effects (e.g., it contains a function that changes a global variable), then an unexpected answer may be obtained.

2. Short-Circuit Code

In short-circuit (or jumping) code, the boolean operators &&, I I, and ! trans-late into jumps. The operators themselves do not appear in the code; instead, the value of a boolean expression is represented by a position in the code se-quence.

Example 6.21 :     The    statement

i f      (  x    <  100  ||  x >  200 && x  != y  )  x = 0;

might be translated into the code of Fig. 6.34. In this translation, the boolean expression is true if control reaches label L₂. If the expression is false, control goes immediately to L_u skipping L₂ and the assignment x = 0.

3. Flow-of-Control Statements

We now consider the translation of boolean expressions into three-address code in the context of statements such as those generated by the following grammar:

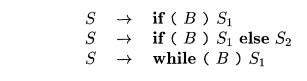
In these productions, nonterminal B represents a boolean expression and non-terminal S represents a statement.

This grammar generalizes the running example of while expressions that we introduced in Example 5.19. As in that example, both B and S have a synthe-sized attribute code, which gives the translation into three-address instructions. For simplicity, we build up the translations B.code and S.code as strings, us-ing syntax-directed definitions. The semantic rules defining the code attributes could be implemented instead by building up syntax trees and then emitting code during a tree traversal, or by any of the approaches outlined in Section 5.5.

The translation of if (B) S1 consists of B.code followed by Si.code,  as illustrated in Fig. 6.35(a). Within B.code are jumps based on the value of B.  If B is true, control flows to the first instruction of Si.code, and if B is false, control flows to the instruction immediately following S1 . code.

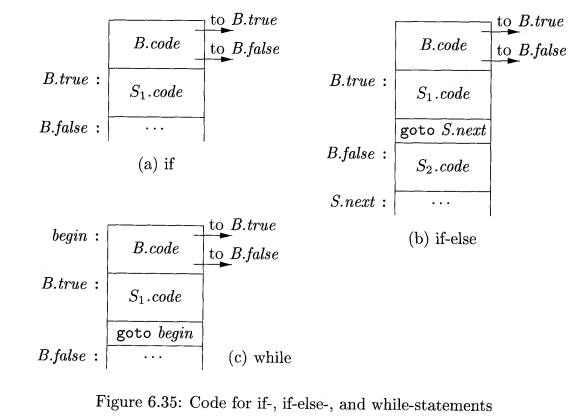
The labels for the jumps in B.code and S.code are managed using inherited attributes. With a boolean expression B, we associate two labels: B.true, the label to which control flows if B is true, and B.false, the label to which control flows if B is false. With a statement S, we associate an inherited attribute S.next denoting a label for the instruction immediately after the code for S. In some cases, the instruction immediately following S.code is a jump to some label L. A jump to a jump to L from within S.code is avoided using S.next.

The syntax-directed definition in Fig. 6.36-6.37 produces three-address code for boolean expressions in the context of if-, if-else-, and while-statements.

We assume that newlabelQ creates a new label each time it is called, and that label(L) attaches label L to the next three-address instruction to be generated.

 A program consists of a statement generated by P -> S. The semantic rules associated with this production initialize S.next to a new label. P.code consists of S.code followed by the new label S.next. Token assign in the production S —> assign is a placeholder for assignment statements. The translation of assignments is as discussed in Section 6.4; for this discussion of control flow, S.code is simply assign.code.

In translating S ->• if (B) Si, the semantic rules in Fig. 6.36 create a new label B.true and attach it to the first three-address instruction generated for the statement Si, as illustrated in Fig. 6.35(a). Thus, jumps to B.true within the code for B will go to the code for Si. Further, by setting B.false to S.next, we ensure that control will skip the code for Si if B evaluates to false.

In translating the if-else-statement S if (B) Si else S 2 , the code for the boolean expression B has jumps out of it to the first instruction of the code for 51 if B is true, and to the first instruction of the code for S2 if B is false, as illustrated in Fig. 6.35(b). Further, control flows from both Si and S2 to the three-address instruction immediately following the code for S — its label is given by the inherited attribute S.next. An explicit goto S.next appears after the code for Si to skip over the code for S 2 . No goto is needed after S 2 , since Si.next is the same as S.next.

The code for S —>• while (B) Si is formed from B.code and Si.code as shown in Fig. 6.35(c). We use a local variable begin to hold a new label attached to the first instruction for this while-statement, which is also the first instruction for B. We use a variable rather than an attribute, because begin is local to the semantic rules for this production. The inherited label S.next marks the instruction that control must flow to if B is false; hence, B.false is set to be S.next. A new label B.true is attached to the first instruction for Si; the code for B generates a jump to this label if B is true. After the code for Si we place the instruction goto begin, which causes a jump back to the beginning of the code for the boolean expression. Note that Si.next is set to this label begin, so jumps from within Si.code can go directly to begin.

 The code for S -» Si S2 consists of the code for Si followed by the code for S 2 . The semantic rules manage the labels; the first instruction after the code for Si is the beginning of the code for S 2 ; and the instruction after the code for 52 is also the instruction after the code for S.

 We discuss the translation of flow-of-control statements further in Section 6.7. There we shall see an alternative method, called "backpatching," which emits code for statements in one pass.

4. Control-Flow Translation of Boolean Expressions

The semantic rules for boolean expressions in Fig. 6.37 complement the semantic rules for statements in Fig. 6.36. As in the code layout of Fig. 6.35, a boolean expression B is translated into three-address instructions that evaluate B using creates labels only when they are needed. Alternatively, unnecessary labels can be eliminated during a subsequent optimization phase.

conditional and unconditional jumps to one of two labels: B.true if B is true, and B.false if B is false.

The fourth production in Fig. 6.37, B E1 rel E2, is translated directly into a comparison three-address instruction with jumps to the appropriate places. For instance, B of the form a < b translates into:

if a < b goto B.true 

goto B.false

The remaining productions for B are translated as follows:

1. Suppose B is of the form B1 || B2. If Bi is true, then we immediately know that B itself is true, so Bi.true is the same as B.true. If Bi is false, then B2 must be evaluated, so we make Bi.false be the label of the first instruction in the code for B2. The true and false exits of B2 are the same as the true and false exits of B, respectively.

2. The  translation  of B1  && B2 is similar.

3. No code is needed for an expression B of the form 1B1.  just interchange  the true and false exits of B to get the true and false exits of B1.

    The constants t r u e and false translate into jumps to B.true and B.false, respectively.

Example 6.22 :  Consider again the following statement from Example 6.21:

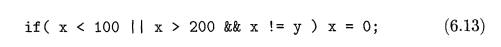
Using the syntax-directed definitions in Figs. 6.36 and 6.37 we would obtain the code in Fig. 6.38.

The statement (6.13) constitutes a program generated by P -> S from Fig. 6.36. The semantic rules for the production generate a new label L1 for the instruction after the code for S. Statement S has the form if (B) Si, where Si is x = 0;, so the rules in Fig. 6.36 generate a new label L2 and attach it to the first (and only, in this case) instruction in Si.code, which is x = 0.

 Since I I has lower precedence than kk, the boolean expression in (6.13) has the form Bi 1 1 B2, where Bi is x < 100. Following the rules in Fig. 6.37, Bi.true is L2, the label of the assignment x = 0; . Bi.false is a new label L3 , attached to the first instruction in the code for B2.

Note that the code generated is not optimal, in that the translation has three more instructions (goto's) than the code in Example 6.21. The instruction goto L3 is redundant, since L 3 is the label of the very next instruction. The two goto Li instructions can be eliminated by using i f F a l s e instead of if instructions, as in Example 6.21.

5. Avoiding Redundant Gotos

In Example 6.22, the comparison x > 200 translates into the code fragment:

This i f F a l s e instruction takes advantage of the natural flow from one instruction to the next in sequence, so control simply  "falls through"  to label L₄    if x > 200 is false, thereby avoiding a jump .

In the code layouts for if- and while-statements in Fig. 6.35, the code for statement S± immediately follows the code for the boolean expression B. By using a special label fall (i.e., "don't generate any jump"), we can adapt the semantic rules in Fig. 6.36 and 6.37 to allow control to fall through from the code for B to the code for Si . The new rules for S -> if (B) Si in Fig. 6.36 set B.true to fall:

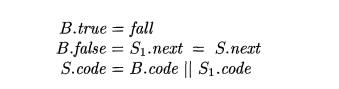
Similarly, the rules for if-else- and while-statements also set B.true to fall We now adapt the semantic rules for boolean expressions to allow control to fall through whenever possible. The new rules for B —> E1 rel E2 in Fig. 6.39 generate two instructions, as in Fig. 6.37, if both B.true and B.false are explicit labels; that is, neither equals fall. Otherwise, if B.true is an explicit label, then B.false must be fall, so they generate an if instruction that lets control fall through if the condition is false. Conversely, if B.false is an explicit label, then they generate an i f F a l s e instruction. In the remaining case, both B.true and B.false are fall, so no jump in generated.9

In the new rules for B Bi II B2 in Fig. 6.40, note that the meaning of label fall for B is different from its meaning for Bi. Suppose B.true is fall; i.e, control falls through B, if B evaluates to true. Although B evaluates to true if Bi does, Bi.true must ensure that control jumps over the code for B2 to get to the next instruction after B.

On the other hand, if Bi evaluates to false, the truth-value of B is determined by the value of B2, so the rules in Fig. 6.40 ensure that Bi.false corresponds to control falling through from Bi to the code for B2.

The semantic rules are for B -» Bi kk B2 are similar to those in Fig. 6.40.

We leave them as an exercise.

Example 6.23 : With the new rules using the special label fall, the program (6.13) from Example 6.21

As in Example 6.22, the rules for P ->• S create label Li. The difference from Example 6.22 is that the inherited  attribute B.true is fall when the semantic rules for B  ->  B1 || B2    are applied  (B.false is Li). The rules in Fig.  6.40 create a new label L2    to allow a jump over the code for B2 if i?i  evaluates to  true.  Thus,  Bi.true is L2 and Bi.false is /a//,  since £?2 must be evaluated if Bi is false.

The production B —>• E± rel _E₂ that generates x < 100 is therefore reached with B.true = L₂ and B.false = /a//. With these inherited labels, the rules in Fig. 6.39 therefore generate a single instruction if x < 100 goto L₂ .

6. Boolean Values and Jumping Code

The focus in this section has been on the use of boolean expressions to alter the flow of control in statements. A boolean expression may also be evaluated for its value, as in assignment statements such as x = t r u e ; or x = a<b; .

A clean way of handling both roles of boolean expressions is to first build a syntax tree for expressions, using either of the following approaches:

1. Use two passes. Construct a complete syntax tree for the input, and then walk the tree in depth-first order, computing the translations specified by the semantic rules.

2. Use one pass for statements, but two passes for expressions. With this approach, we would translate E in while (E) Si before Si is examined. The translation of E, however, would be done by building its syntax tree and then walking the tree.

The following grammar has a single nonterminal E for expressions:

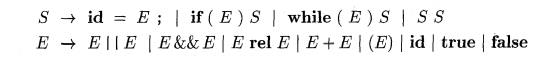
Nonterminal E governs the flow of control in S -» while (E) Si. The same nonterminal E denotes a value in S--> id  = E; and E —>• E  + E.

We can handle these two roles of expressions by using separate code-genera-tion functions. Suppose that attribute E.n denotes the syntax-tree node for an expression E and that nodes are objects. Let method jump generate jumping code at an expression node, and let method rvalue generate code to compute the value of the node into a temporary.

When E appears in S ->• while (E) Si, method jump is called at node E.n. The implementation of jump is based on the rules for boolean expressions in Fig. 6.37. Specifically, jumping code is generated by calling E.n.jump(t, /), where t is a new label for the first instruction of Si.code and / is the label S.next.

When E appears in S —> id = E;, method rvalue is called at node E.n. If E has the form Ei+E2, the method call E.n.rvalueQ generates code as discussed in Section 6.4. If E has the form E1 && E2, we first generate jumping code for E and then assign true or false to a new temporary t at the true and false exits, respectively, from the jumping code.

For example, the assignment x = a < b & & c < d can be implemented by the code in Fig. 6.42.

7. Exercises for Section 6.6

Exercise 6 . 6 . 1 : Add rules to the syntax-directed definition of Fig. 6.36 for the following control-flow constructs:

a) A repeat-statment repeat  S while B.

  b) A for-loop for (Si; B;      S₂)  S₃.

Exercise 6 . 6 . 2 : Modern machines try to execute many instructions at the same time, including branching instructions. Thus, there is a severe cost if the machine speculatively follows one branch, when control actually goes another way (all the speculative work is thrown away). It is therefore desirable to min-imize the number of branches. Notice that the implementation of a while-loop in Fig. 6.35(c) has two branches per interation: one to enter the body from the condition B and the other to jump back to the code for B. As a result, it is usually preferable to implement while (B) S as if it were if (B) { repeat S until 1(B) }. Show what the code layout looks like for this translation, and revise the rule for while-loops in Fig. 6.36.

Exercise 6 . 6 . 3 : Suppose that there were an "exclusive-or" operator (true if and only if exactly one of its two arguments is true) in C. Write the rule for this operator in the style of Fig. 6.37.

Exercise 6 . 6 . 4 : Translate the following expressions using the goto-avoiding translation scheme of Section 6.6.5:

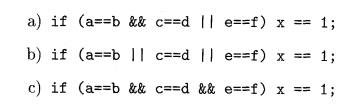
Exercise 6 . 6 . 5 : Give a translation scheme based on the syntax-directed defi-nition in Figs. 6.36 and 6.37.

Exercise 6 . 6 . 6: Adapt the semantic rules in Figs. 6.36 and 6.37 to allow control to fall through, using rules like the ones in Figs. 6.39 and 6.40.

Exercise 6 . 6 . 7: The semantic rules for statements in Exercise 6.6.6 generate unnecessary labels. Modify the rules for statements in Fig. 6.36 to create labels as needed, using a special label deferred to mean that a label has not yet been created. Your rules must generate code similar to that in Example 6.21.

Exercise 6 . 6 . 8 : Section 6.6.5 talks about using fall-through code to minimize the number of jumps in the generated intermediate code. However, it does not take advantage of the option to replace a condition by its complement, e.g., replace if a < b  goto  Li;  g o t o  L2   by if b >= a  goto  L2;  goto  L1.  Develop a SDD that does take advantage of this option when needed.