Three-Address Code

Three-Address Code

1 Addresses and Instructions

2 Quadruples

3 Triples

4 Static Single-Assignment Form

5 Exercises for Section 6.2

In three-address code, there is at most one operator on the right side of an instruction; that is, no built-up arithmetic expressions are permitted. Thus a source-language expression like x+y*z might be translated into the sequence of three-address instructions

where ti and t₂ are compiler-generated temporary names. This unraveling of multi-operator arithmetic expressions and of nested flow-of-control statements makes three-address code desirable for target-code generation and optimization, as discussed in Chapters 8 and 9. The use of names for the intermediate values computed by a program allows three-address code to be rearranged easily.

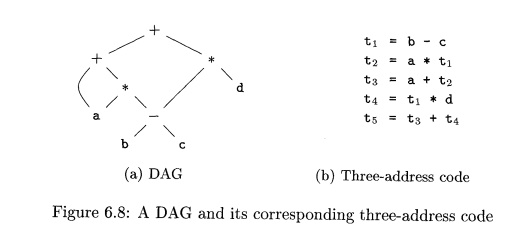
Example 6 . 4 : Three-address code is a linearized tree or representation of a syntax to a DAG in which explicit names correspond graph. The DAG the interior nodes of the in Fig. 6.3 is repeated in Fig. 6.8, ing three-address code together with a correspond-sequence.

1. Addresses and Instructions

Three-address code is built from two concepts: addresses and instructions. In object-oriented terms, these concepts correspond to classes, and the various kinds of addresses and instructions correspond to appropriate subclasses. Alternatively,  three -address code can be implemented  using records with fields for the addresses; records called quadruples and triples are discussed briefly in Section 6.2.2.

An address can be one of the following:

• A name. For convenience, we allow source-program names to appear as addresses in three-address code. In an implementation, a source name is replaced by a pointer to its symbol-table entry, where all information about the name is kept.

• A constant. In practice, a compiler must deal with many different types of constants and variables. Type conversions within expressions are con-sidered in Section 6.5.2.

• A compiler-generated temporary. It is useful, especially in optimizing com-pilers, to create a distinct name each time a temporary is needed. These temporaries can be combined, if possible, when registers are allocated to variables.

We now consider the common three-address instructions used in the rest of this book. Symbolic labels will be used by instructions that alter the flow of control. A symbolic label represents the index of a three-address instruction in the sequence of instructions. Actual indexes can be substituted for the labels, either by making a separate pass or by "backpatching," discussed in Section 6.7. Here is a list of the common three-address instruction forms:

    Assignment instructions of the form x = y op z, where op is a binary arithmetic or logical operation, and x, y, and z are addresses.

    Assignments of the form x = op y, where op is a unary operation. Essen-tial unary operations include unary minus, logical negation, shift opera-tors, and conversion operators that, for example, convert an integer to a floating-point number.

3.  Copy instructions of the form x = y,  where x is assigned the value of y.

4. An unconditional jump g o t o L.  The three-address instruction with label

L is the next to be executed.

5. Conditional jumps of the form if x goto L and if F a l s e x goto L. These instructions execute the instruction with label L next if x is true and false, respectively. Otherwise, the following three-address instruction in sequence is executed next, as usual.

6. Conditional jumps such as if x relop y goto L, which apply a relational operator (<, ==, >=, etc.) to x and y, and execute the instruction with label L next if x stands in relation relop to y. If not, the three-address instruction following if x relop y goto L is executed next, in sequence.

7. Procedure calls and returns are implemented using the following instruc-tions: param x for parameters; c a l l p , n and y = c a l l p , n for procedure and function calls, respectively; and r e t u r n y, where y, representing a returned value, is optional. Their typical use is as the sequence of three-address instructions

generated  as  part  of a  call  of the  procedure         p(x1,x2, • • •       ,xn).  The   integer n,  indicating the number of actual parameters         in  " c a l l p, n,"  is not redundant because calls can be              nested.       That  is,      some of the first param statements could be parameters of a call that comes after p returns its value;  that value becomes another parameter of the later call.          The implementation of procedure calls is outlined in Section 6.9.

8.      Indexed copy instructions of the form   x = y[il       and   xlil    = y.   The          instruction x = y lil  sets x to the value in       the location i       memory     units          beyond location y.  The instruction x[i"] =y  sets the contents of the location i units beyond x to the value of y.

9. Address and pointer assignments of the form x = &y, x = * y, and * x - y.

The instruction x = ky sets the r-value of x     to be the location (/-value) of y?  Presumably y  is  a name,  perhaps a temporary,  that  denotes an expression with an /-value such as A[i] [ j ] ,        and # is a pointer name or temporary.  In the instruction x  =  *y,  presumably y is  a pointer or a temporary whose r-value is a location.      The   r-value of x is made equal to the contents of that        location.    Finally,      * x    = y sets the r-value of the object pointed to by x         to the r-value of y.

Example 6 . 5 :  Consider the        statement

do  i  =       i + 1 ;  while  ( a [ i ]    <  v ) ;

Two possible translations of this statement are shown in Fig. 6.9. The transla-tion in Fig. 6.9 uses a symbolic label L, attached to the first instruction. The translation in (b) shows position numbers for the instructions, starting arbitrar-ily at position 100. In both translations, the last instruction is a conditional jump to the first instruction. The multiplication i * 8 is appropriate for an array of elements that each take 8 units of space.

The choice of allowable operators is an important issue in the design of an intermediate form. The operator set clearly must be rich enough to implement the operations in the source language. Operators that are close to machine instructions make it easier to implement the intermediate form on a target machine. However, if the front end must generate long sequences of instructions for some source-language operations, then the optimizer and code generator may have to work harder to rediscover the structure and generate good code for these operations.

2. Quadruples

The description of three-address instructions specifies the components of each type of instruction, but it does not specify the representation of these instruc-tions in a data structure. In a compiler, these instructions can be implemented as objects or as records with fields for the operator and the operands. Three such representations are called "quadruples," "triples," and "indirect triples."

A quadruple (or just "quad!') has four fields, which we call op, arg_1: arg₂, and result. The op field contains an internal code for the operator. For instance, the three-address instruction x = y + z is represented by placing + in op, y in arg₁, z in arg₂, and x in result. The following are some exceptions to this rule:

1. Instructions with unary operators like x = minus y or x = y do not use arg2. Note that for a copy statement like x = y, op is =, while for most other operations, the assignment operator is implied.

2. Operators like p a r am use neither arg2  nor result.

3. Conditional and unconditional jumps put the target label in  result.

Example 6 . 6: Three-address  code for  the  assignment  a =  b * - c + b * - c ; appears in Fig. 6.10(a).  The special operator minus is used to distinguish the unary minus operator, as in - c, from the binary minus operator, as in b - c. Note that the unary-minus "three-address" statement has only two addresses, as does the copy statement a = t ₅ .

The quadruples in Fig. 6.10(b) implement the three-address code in (a).

For readability, we use actual identifiers like a, b, and c in the fields  argx, arg₂, and result in Fig. 6.10(b), instead of pointers to their symbol-table entries. Temporary names can either by entered into the symbol table like programmer-defined names, or they can be implemented as objects of a class Temp with its own methods.

3. Triples

A triple has only three fields, which we call op, arg_x, and arg₂- Note that the result field in Fig. 6.10(b) is used primarily for temporary names. Using triples, we refer to the result of an operation x op y by its position, rather than by an explicit temporary name. Thus, instead of the temporary ti in Fig. 6.10(b), a triple representation would refer to position (0). Parenthesized numbers represent pointers into the triple structure itself. In Section 6.1.2, positions or pointers to positions were called value numbers.

Triples are equivalent to signatures in Algorithm 6.3. Hence, the DAG and triple representations of expressions are equivalent. The equivalence ends with expressions, since syntax-tree variants and three-address code represent control flow quite differently.

E x a m p l e 6 . 7 : The syntax tree and triples in Fig. 6.11 correspond to the three-address code and quadruples in Fig. 6.10. In the triple representation in Fig. 6.11(b), the copy statement a = t₅ is encoded in the triple representation by placing a in the arc^ field and (4) in the arg₂ field. •

A ternary operation like x[i] = y requires two entries in the triple structure; for example, we can put x and i in one triple and y in the next. Similarly, x = y{.%] can implemented by treating it as if it were the two instructions

Why Do We Need Copy Instructions?

A simple algorithm for translating expressions generates copy instructions for assignments, as in Fig. 6.10(a), where we copy ts into a rather than assigning t₂ +14 to a directly. Each subexpression typically gets its own, new temporary to hold its result, and only when the assignment operator = is processed do we learn where to put the value of the complete expression. A code-optimization pass, perhaps using the DAG of Section 6.1.1 as an intermediate form, can discover that can be replaced by a.

t = y[i] and x = t, where i i s a compiler-generated temporary. Note that the temporary t does not actually appear in a triple, since temporary values are referred to by their position in the triple structure.

A benefit of quadruples over triples can be seen in an optimizing compiler, where instructions are often moved around. With quadruples, if we move an instruction that computes a temporary t, then the instructions that use t require no change. With triples, the result of an operation is referred to by its position, so moving an instruction may require us to change all references to that result. This problem does not occur with indirect triples, which we consider next.

Indirect triples consist of a listing of pointers to triples, rather than a listing of triples themselves. For example, let us use an array instruction to list pointers to triples in the desired order. Then, the triples in Fig. 6.11(b) might be represented as in Fig. 6.12.

With indirect triples, an optimizing compiler can move an instruction by reordering the instruction list, without affecting the triples themselves. When implemented in Java, an array of instruction objects is analogous to an indi-rect triple representation, since Java treats the array elements as references to objects.

4. Static Single-Assignment Form

Static single-assignment form (SSA) is an intermediate representation that fa-cilitates certain code optimizations. Two distinctive aspects distinguish SSA from three-address code. The first is that all assignments in SSA are to vari-ables with distinct names; hence the term static single-assigment. Figure 6.13 shows the same intermediate program in three-address code and in static single-assignment form. Note that subscripts distinguish each definition of variables p and q in the SSA representation.

The same variable may be defined in two different control-flow paths in a program. For example, the source program

if (  f l a g )  x = -1;  e l s e x =  1;

y  = x  *  a;

has two control-flow paths in which the variable x gets defined. If we use different names for x in the true part and the false part of the conditional statement, then which name should we use in the assignment y = x * a? Here is where the second distinctive aspect of SSA comes into play. SSA uses a notational convention called the (^-function to combine the two definitions of x:

if ( f l a g ) xi = -1; e l s e x₂ = 1; x ₃ = ϕ ( x 1 , x ₂ ) ;

Here, ϕ(x1,x2) has the value x2 if the control flow passes through the true part of the conditional and the value x2 if the control flow passes through the false part. That is to say, the ϕ-function returns the value of its argument that corresponds to the control-flow path that was taken to get to the assignment-statement containing the ϕ-function.

5. Exercises for Section 6.2

Exercise 6 . 2 . 1 : Translate the arithmetic expression a + - (a -b- c) into:

A syntax tree.

Quadruples.

         Triples.

 Indirect triples.

Exercise 6 . 2 . 2: Repeat Exercise 6.2.1 for the following assignment state-ments:

       a = b[i]  +  c[j].

 a[i]  =  b*c  -  b*d.

Hi.  x  =  f (y+1)          +  2.

  x = *p  + &y.

  Exercise 6 . 2 . 3: Show how to transform a three-address code sequence into one in which each defined variable gets a unique variable name.