Type Checking

Type Checking

1 Rules for Type Checking

 2 Type Conversions

 3 Overloading of Functions and Operators

 4 Type Inference and Polymorphic Functions

 5 An Algorithm for Unification

 6 Exercises for Section 6.5

To do type checking a compiler needs to assign a type expression to each com-ponent of the source program. The compiler must then determine that these type expressions conform to a collection of logical rules that is called the type system for the source language.

Type checking has the potential for catching errors in programs. In principle, any check can be done dynamically, if the target code carries the type of an element along with the value of the element. A sound type system eliminates the need for dynamic checking for type errors, because it allows us to determine statically that these errors cannot occur when the target program runs. An implementation of a language is strongly typed if a compiler guarantees that the programs it accepts will run without type errors.

Besides their use for compiling, ideas from type checking have been used to improve the security of systems that allow software modules to be imported and executed. Java programs compile into machine-independent bytecodes that include detailed type information about the operations in the bytecodes. Im-ported code is checked before it is allowed to execute, to guard against both inadvertent errors and malicious misbehavior.

1. Rules for Type Checking

Type checking can take on two forms: synthesis and inference. Type synthesis builds up the type of an expression from the types of its subexpressions. It requires names to be declared before they are used. The type of E1 + E₂ is defined in terms of the types of E1 and E₂ • A typical rule for type synthesis has the form

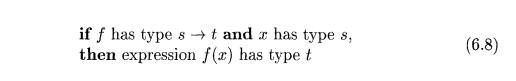
Here, f and x denote expressions, and s ->• t denotes a function from s to t. This rule for functions with one argument carries over to functions with several arguments.   The rule          (6.8) can be adapted for E1 +E2   by viewing it as a function application          add(Ei,E2).Q

Type inference determines the type of a language construct from the way it is used.  Looking ahead to the examples in Section      6.5.4, let null be a function that tests whether a   list is empty.  Then,     from the usage null(x),         we can tell that x must be a list. The type of the elements of x        is not known;     all we know is that x must be a list of elements of some type that is presently unknown. Variables representing type expressions allow us to talk about unknown types. We shall use Greek letters a, (3, • • •          for type variables in type expressions.

A typical rule for type inference has the form

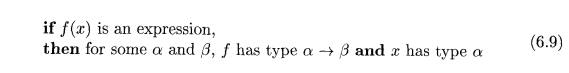
Type inference is needed for languages like ML, which check types, but do not require names to be declared.

We shall use the term "synthesis" even if some context information is used to determine types. With overloaded functions, where the same name is given to more than one function, the context of E1 + E2 may also need to be considered in some languages.

In this section, we consider type checking of expressions. The rules for checking statements are similar to those for expressions. For example, we treat the conditional statement "if (E) S;" as if it were the application of a function if to E and S. Let the special type void denote the absence of a value. Then function if expects to be applied to a boolean and a void; the result of the application is a void.

2. Type Conversions

Consider expressions like x + i, where x is of type float and i is of type inte-ger. Since the representation of integers and floating-point numbers is different within a computer and different machine instructions are used for operations on integers and floats, the compiler may need to convert one of the operands of + to ensure that both operands are of the same type when the addition occurs.

Suppose that integers are converted to floats when necessary, using a unary operator ( f l o a t ) . For example, the integer 2 is converted to a float in the code for the expression 2*3.14:

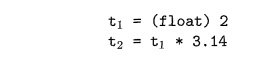
We can extend such examples to consider integer and float versions of the operators; for example, i n t * for integer operands and float * for floats.

Type synthesis will be illustrated by extending the scheme in Section 6.4.2 for translating expressions. We introduce another attribute E.type, whose value

is either integer or float. The rule associated with E -- > E1 + E2 builds on the pseudocode

As the number of types subject to conversion increases, the number of cases increases rapidly. Therefore with large numbers of types, careful organization of the semantic actions becomes important.

Type conversion rules vary from language to language. The rules for Java in Fig. 6.25 distinguish between widening conversions, which are intended to preserve information, and narrowing conversions, which can lose information. The widening rules are given by the hierarchy in Fig. 6.25(a): any type lower in the hierarchy can be widened to a higher type. Thus, a char can be widened to an int or to a float, but a char cannot be widened to a short. The narrowing rules are illustrated by the graph in Fig. 6.25(b): a type s can be narrowed to a type t if there is a path from s to t. Note that char, short, and byte are pairwise convertible to each other.

Conversion from one type to another is said to be implicit if it is done automatically by the compiler. Implicit type conversions, also called coercions,

are limited in many languages to widening conversions. Conversion is said to be explicit if the programmer must write something to cause the conversion. Explicit conversions are also called casts.

The semantic action for checking E -» E1 + E2    uses two functions:

          max(t1,t2) takes two types ti and t2 and returns the maximum (or least upper bound) of the two types in the widening hierarchy. It declares an error if either t1 or t2   is not in the hierarchy;          e.g., if either type is an array or a pointer type.        

2.  widen(a, t, w)  generates  type  conversions if     needed  to widen  an address a of type t into a value of type w. It returns a itself if t and w are the same type. Otherwise, it generates an instruction to do the conversion and place the result in a temporary t, which is returned as the result. Pseudocode for widen, assuming that the only types are integer and float, appears in Fig. 6.26.

The semantic  action for  E -» E1  + E2    in  Fig.  6.27 illustrates  how type conversions can be added to the scheme in Fig. 6.20 for translating expressions.

In the semantic action, temporary variable a1  is either Ei.addr, if the type of Ei does not need to be converted to the type of E, or a new temporary variable returned by widen if this conversion is necessary. Similarly, a2    is either E2.addr or a new temporary holding the type-converted value of E2. Neither conversion is needed if both types are integer or both are float. In general, however, we could find that the only way to add values of two different types is to convert them both to a third type.

3. Overloading of Functions and Operators

An overloaded symbol has different meanings depending on its context. Over-loading is resolved when a unique meaning is determined for each occurrence of a name. In this section, we restrict attention to overloading that can be resolved by looking only at the arguments of a function, as in Java.

Example 6.13 : The + operator in Java denotes either string concatenation or addition, depending on the types of its operands. User-defined functions can be overloaded as well, as in

Note that we can choose between these two versions of a function e r r by looking at their arguments.

The following is a type-synthesis rule for overloaded functions:

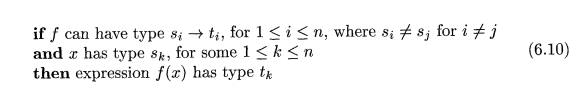
The value-number method of Section 6.1.2 can be applied to type expressions to resolve overloading based on argument types, efficiently. In a DAG representing a type expression, we assign an integer index, called a value num-ber, to each node. Using Algorithm 6.3, we construct a signature for a node, consisting of its label and the value numbers of its children, in order from left to right. The signature for a function consists of the function name and the types of its arguments. The assumption that we can resolve overloading based on the types of arguments is equivalent to saying that we can resolve overloading based on signatures.

It is not always possible to resolve overloading by looking only at the argu-ments of a function. In Ada, instead of a single type, a subexpression standing alone may have a set of possible types for which the context must provide suffi-cient information to narrow the choice down to a single type (see Exercise 6.5.2).

4. Type Inference and Polymorphic Functions

Type inference is useful for a language like ML, which is strongly typed, but does not require names to be declared before they are used. Type inference ensures that names are used consistently.

The term "polymorphic" refers to any code fragment that can be executed with arguments of different types. In this section, we consider parametric poly-morphism, where the polymorphism is characterized by parameters or type variables. The running example is the ML program in Fig. 6.28, which defines a function length. The type of length can be described as, "for any type a, length maps a list of elements of type a to an integer."

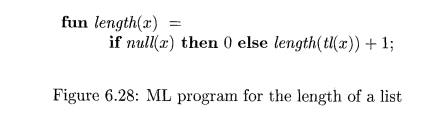
E x a m p l e 6 . 1 4 :  In Fig. 6.28, the keyword fun introduces a function definition;

functions can be recursive. The program fragment defines function length with one parameter x. The body of the function consists of a conditional expression. The predefined function null tests whether a list is empty, and the predefined function tl (short for "tail") returns the remainder of a list after the first element is removed.

The function  length determines the length or number of elements of a list x.  All elements of a list must have the same type, but length can be applied to lists whose elements are of any one type.  In the following expression, length is applied to two different types of lists (list elements are enclosed within "[" and "]"): 

length{[" sun", "mon", "tue"]) + length([10,9,8, 7]) (6.11)

The list of strings has length 3 and the list of integers has length 4, so expres-sion (6.11) evaluates to 7. •

Using the symbol " (read as "for any type") and the type constructor list, the type of length can be written as

The " symbol is the universal quantifier, and the    type variable to which it is applied is said to be bound by it. Bound variables can be renamed at will, provided all occurrences of the variable are renamed. Thus, the type expression

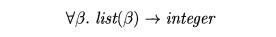
is equivalent to (6.12). A type expression with a V symbol in it will be referred to informally as a "polymorphic type."

Each time a polymorphic function is applied, its bound type variables can denote a different type. During type checking, at each use of a polymorphic type we replace the bound variables by fresh variables and remove the universal quantifiers.

The next example informally infers a type for length, implicitly using type inference rules like (6.9), which is repeated here:

E x a m p l e 6.15 : The abstract syntax tree in Fig. 6.29 represents the definition of length in Fig. 6.28. The root of the tree, labeled fun, represents the function definition. The remaining nonleaf nodes can be viewed as function applications. The node labeled -+- represents the application of the operator + to a pair of children. Similarly, the node labeled if represents the application of an operator if to a triple formed by its children (for type checking, it does not matter that either the then or the else part will be evaluated, but not both).

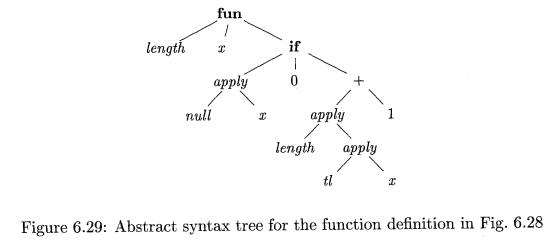
From the body of function length, we can infer its type.  Consider the children of the node labeled if, from left to right. Since  null expects to be applied to lists, x must be a list. Let us use variable a as a placeholder for the type of the list elements; that is, x has type "list of a."

Substitutions, Instances, and Unification

If t is a type expression and 5 is a substitution (a mapping from type vari-ables to type expressions), then we write S(i) for the result of consistently replacing all  occurrences  of each  type  variable  a  in  t  by  S(a). S(t)  is called an  instance of t.  For example,  list(integer) is an instance of list(a), since it is the result of substituting integer for a in list(a).  Note, however, that integer —> float is not an instance of a —> a, since a substitution must replace all occurrences of a by the same type expression.

Substitution 5 is  a unifier of type expressions t1  and  t2 if S(t1) = S(t2).  5 is the most general unifier of t1 and t2 if for any other unifier of ri  and t2, say S", it is the case that for any t, S'(t) is an instance of S(t).

In words, S' imposes more constraints on t than S does.  

If null(x) is true,  then length(x) is  0. Thus, the type of length must  be "function from list of a to integer." This inferred type is consistent with the usage of length in the else part, length(tl{x)) + 1. •

Since variables can appear in type expressions, we have to re-examine the notion of equivalence of types.  Suppose E1  of type s s' is applied to E2    of type t. Instead of simply determining the equality of s and t, we must  "unify" them. Informally, we determine whether s and t can be made structurally equivalent by replacing the type variables in s and t by type expressions.

A substitution is a mapping from type variables to type expressions. We write S(t) for the result of applying the substitution S to the variables in type expression t; see the box on "Substitutions, Instances, and Unification." Two type expressions t1  and t2     unify if there exists some substitution 5 such that S(ti) = S(t2).  In practice, we are interested in the most general unifier, which is a substitution that imposes the fewest constraints on the variables in the expressions. See Section 6.5.5 for a unification algorithm.

Algorithm 6.16 : Type inference for polymorphic functions.

INPUT : A program consisting of a sequence of function definitions followed by an expression to be evaluated. An expression is made up of function applications and names, where names can have predefined polymorphic types.

OUTPUT : Inferred types for the names in the program.

METHOD : For simplicity, we shall deal with unary functions only. The type of a function  f(xi,x2)  with two parameters can be represented by a type expression si x s₂   ->• t, where si and s2   are the types of x1 and x2, respectively, and t is the type of the result f(xi,x2).  An expression / ( a , b)  can be checked by matching the type of a with si and the type of b with s₂.

Check the function definitions and the expression in the input sequence. Use the inferred type of a function if it is subsequently used in an expression.

•        For a function definition          fun i d i ( i d 2 ) = E, create      fresh type variables a and (3.  Associate the type a -> (3 with the function idi, and the type a with the parameter i d 2 .          Then, infer a type for expression      E.  Suppose a denotes type s and j3 denotes type t after type inference for E.  The inferred type of function idi is s       -> t.  Bind any type variables that remain unconstrained in s -» t by V quantifiers.

•        For a function application Ei(E2),  infer types for E1   and E2.       Since Ei  is used as a function, its type must have the form s -»• s'.  (Technically, the type of E1 must unify with j3          7, where j3 and 7 are new type variables). Let t be the inferred type of E1.  Unify s and t.  If unification fails, the expression has a type error. Otherwise, the inferred type of E1(E2) is s'.

  For each occurrence of a polymorphic function, replace the bound vari-ables in its type by distinct fresh variables and remove the V quantifiers.

The resulting type expression is the inferred type of this occurrence.

For a name that is encountered for the first time, introduce a fresh variable for its type.

E x a m p l e 6 . 1 7 : In Fig. 6.30, we infer a type for function length. The root of the syntax tree in Fig. 6.29 is for a function definition, so we introduce variables 13 and 7, associate the type j3 7 with function length, and the type (3 with x; see lines 1-2 of Fig. 6.30.

At the right child of the root, we view if as a polymorphic function that is applied to a triple, consisting of a boolean and two expressions that represent the t h e n and else parts. Its type is VCK. boolean x a x a —> a.

Each application of a polymorphic function can be to a different type, so we make up a fresh variable ai (where i is from "if") and remove the V; see line 3 of Fig. 6.30. The type of the left child of if must unify with boolean, and the types of its other two children must unify with on.

The predefined function null has type Vet. list(a) boolean. We use a fresh type variable an (where n is for "null") in place of the bound variable a; see line 4. From the application of null to x, we infer that the type f3 of x must match list(an); see line 5.

 At the first child of if, the type boolean for null(x) matches the type expected by if. At the second child, the type a* unifies with integer; see line 6.

 Now, consider the subexpression length(tl(x)) + 1. We make up a fresh variable at (where t is for "tail") for the bound variable a in the type of tl; see line 8. From the application tl(x), we infer list(at) = (3 = list(an); see line 9.

 Since length(tl(x)) is an operand of +, its type 7 must unify with integer; see line 10. It follows that the type of length is list(an) ->• integer. After the

function definition is checked, the type variable a_n remains in the type of length. Since no assumptions were made about a_n, any type can be substituted for it when the function is used. We therefore make it a bound variable and write

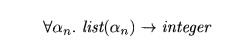
for the type of length.    •

5. An Algorithm for Unification

Informally, unification is the problem of determining whether two expressions s and t can be made identical by substituting expressions for the variables in s and t. Testing equality of expressions is a special case of unification; if s and t have constants but no variables, then s and t unify if and only if they are identical. The unification algorithm in this section extends to graphs with cycles, so it can be used to test structural equivalence of circular types . ⁷

We shall implement a graph-theoretic formulation of unification, where types are represented by graphs. Type variables are represented by leaves and type constructors are represented by interior nodes. Nodes are grouped into equiv-alence classes; if two nodes are in the same equivalence class, then the type expressions they represent must unify. Thus, all interior nodes in the same class must be for the same type constructor, and their corresponding children must be equivalent.

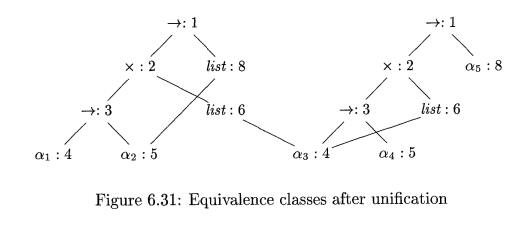
Example 6.18 :  Consider the two type expressions

The two expressions are represented by the two nodes labeled - »: 1 in Fig. 6.31. The integers at the nodes indicate the equivalence classes that the nodes belong to after the nodes numbered 1 are unified. •

Algorithm 6 . 1 9 :  Unification of a pair of nodes in a type graph.

INPUT : A graph representing a type and a pair of nodes m and n to be unified.

OUTPUT : Boolean value true if the expressions represented by the nodes m and n unify; false, otherwise.

METHOD : A node is implemented by a record with fields for a binary operator and pointers to the left and right children. The sets of equivalent nodes are maintained using the set field. One node in each equivalence class is chosen to be the unique representative of the equivalence class by making its set field contain a null pointer. The set fields of the remaining nodes in the equivalence class will point (possibly indirectly through other nodes in the set) to the representative. Initially, each node n is in an equivalence class by itself, with n as its own representative node.

The unification algorithm, shown in Fig. 6.32, uses the following two operations on nodes:

 find{n) returns the representative node of the equivalence class currently containing node n.

• union(m, n) merges the equivalence classes containing nodes m and n. If one of the representatives for the equivalence classes of m and n is a non-variable node, union makes that nonvariable node be the representative for the merged equivalence class; otherwise, union makes one or the other of the original representatives be the new representative. This asymme-try in the specification of union is important because a variable cannot be used as the representative for an equivalence class for an expression containing a type constructor or basic type. Otherwise, two inequivalent expressions may be unified through that variable.

The union operation on sets is implemented by simply changing the set field of the representative of one equivalence class so that it points to the represen-tative of the other. To find the equivalence class that a node belongs to, we follow the set pointers of nodes until the representative (the node with a null pointer in the set field) is reached.

Note that the algorithm in Fig. 6.32 uses s = find(m) and t = find(n) rather than m and n, respectively. The representative nodes s and t are equal if m and n are in the same equivalence class. If s and t represent the same basic type, the call unify(m, n) returns true. If s and t are both interior nodes for a binary type constructor, we merge their equivalence classes on speculation and recursively check that their respective children are equivalent. By merging first, we decrease the number of equivalence classes before recursively checking the children, so the algorithm terminates.

The substitution of an expression for a variable is implemented by adding the leaf for the variable to the equivalence class containing the node for that expression. Suppose either m or n is a leaf for a variable. Suppose also that this leaf has been put into an equivalence class with a node representing an expression with a type constructor or a basic type. Then find will return a representative that reflects that type constructor or basic type, so that a variable cannot be unified with two different expressions.

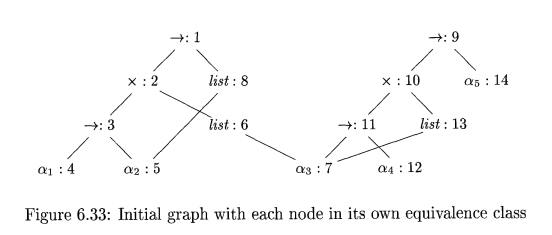
Example     6.20 :  Suppose that the two expressions in Example 6.18 are represented by   the initial graph in Fig. 6.33, where each node is in its own equivalence class.          When  Algorithm 6.19 is applied to compute  unify(l,9),  it  notes that nodes 1 and 9 both represent the same operator. It therefore merges 1 and 9  into  the  same  equivalence       class  and  calls  unify(2,10)  and  unify(8,14).  The result of computing unify(l, 9)   is the graph previously shown in Fig. 6.31.

If Algorithm 6.19 returns true, we can construct a substitution S that acts as the unifier, as follows.  For each variable a, find(a)  gives the node n that is the representative of the equivalence class of a. The expression represented by n is S(a). For example, in Fig. 6.31, we see that the representative for «3 is node 4, which represents a1. The representative for a§ is node 8, which represents list(a.2)- The resulting substitution S is as in Example 6.18.

6. Exercises for Section 6.5

Exercise 6 . 5 . 1 : Assuming that function widen in Fig. 6.26 can handle any of the types in the hierarchy of Fig. 6.25(a), translate the expressions below. Assume that c and d are characters, s and t are short integers, i and j are integers, and x is a float.

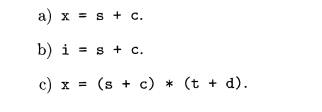
Exercise 6.5.2 : As in Ada, suppose that each expression must have a unique type, but that from a subexpression, by itself, all we can deduce is a set of possible types. That is, the application of function Ei to argument E2, represented by E —> Ei (Ei), has the associated rule

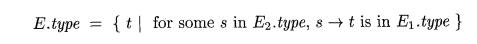
Describe an SDD that determines a unique type for each subexpression by using an attribute type to synthesize a set of possible types bottom-up, and, once the unique type of the overall expression is determined, proceeds top-down to determine attribute unique for the type of each subexpression.