Types and Declarations

Types and Declarations

1 Type Expressions

 2 Type Equivalence

 3 Declarations

 4 Storage Layout for Local Names

 5 Sequences of Declarations

 6 Fields in Records and Classes

 7 Exercises for Section 6.3

The applications of types can be grouped under checking and translation:

• Type checking uses logical rules to reason about the behavior of a program at run time. Specifically, it ensures that the types of the operands match the type expected by an operator. For example, the && operator in Java expects its two operands to be booleans; the result is also of type boolean.

• Translation Applications. From the type of a name, a compiler can de-termine the storage that will be needed for that name at run time. Type information is also needed to calculate the address denoted by an array reference, to insert explicit type conversions, and to choose the right ver-sion of an arithmetic operator, among other things.

In this section, we examine types and storage layout for names declared within a procedure or a class. The actual storage for a procedure call or an object is allocated at run time, when the procedure is called or the object is created. As we examine local declarations at compile time, we can, however, lay out relative addresses, where the relative address of a name or a component of a data structure is an offset from the start of a data area.

1. Type Expressions

Types have structure, which we shall represent using type expressions: a type expression is either a basic type or is formed by applying an operator called a type constructor to a type expression. The sets of basic types and constructors depend on the language to be checked.

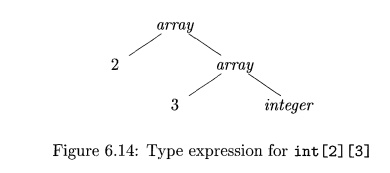
Example 6 . 8 : The array type i n t [2] [3] can be read as "array of 2 arrays of 3 integers each" and written as a type expression array(2, array(3, integer)).

This type is represented by the tree in Fig. 6.14. The operator array takes two parameters, a number and a type.

We shall use the following definition of type expressions:

• A basic type is a type expression. Typical basic types for a language include boolean, char, integer, float, and void; the latter denotes "the absence of a value."

 A type name is a type expression.

 A type expression can be formed by applying the array type constructor to a number and a type expression.

• A record is a data structure with named fields. A type expression can be formed by applying the record type constructor to the field names and their types. Record types will be implemented in Section 6.3.6 by applying the constructor record to a symbol table containing entries for the fields.

A type expression can be formed by using the type constructor —>• for func-tion types. We write s —»• t for "function from type s to type r." Function types will be useful when type checking is discussed in Section 6.5.

Type Names and Recursive Types

Once a class is defined, its name can be used as a type name in C++ or Java; for example, consider Node in the program fragment

p u b l i c class Node { • • • }

p u b l i c   Node  n;

Names can be used to define recursive types, which are needed for data structures such as linked lists. The pseudocode for a list element

class Cell { int  info;  Cell next; ••• }

defines the recursive type Cell as a class that contains a field i n f o and a field next of type Cell. Similar recursive types can be defined in C using records and pointers. The techniques in this chapter carry over to recursive types.

If s and t are type expressions, then their Cartesian product s x t is a type expression. Products are introduced for completeness; they can be used to represent a list or tuple of types (e.g., for function parameters). We assume that x associates to the left and that it has higher precedence than ->.

  Type expressions may contain variables whose values are type expressions. Compiler-generated type variables will be used in Section 6.5.4.

A convenient way to represent a type expression is to use a graph. The value-number method of Section 6.1.2, can be adapted to construct a dag for a type expression, with interior nodes for type constructors and leaves for basic types, type names, and type variables; for example, see the tree in Fig. 6.14.³

2. Type Equivalence

When are two type expressions equivalent? Many type-checking rules have the form, "if two type expressions are equal t h e n return a certain type else error." Potential ambiguities arise when names are given to type expressions and the names are then used in subsequent type expressions. The key issue is whether a name in a type expression stands for itself or whether it is an abbreviation for another type expression.

3 Since type names denote type expressions, they can set up implicit cycles; see the box on "Type Names and Recursive Types." If edges to type names are redirected to the type expressions denoted by the names, then the resulting graph can have cycles due to recursive types.

When type expressions are represented by graphs, two types are structurally equivalent if and only if one of the following conditions is true:

  They are the same basic type.

  They are formed by applying the same constructor to structurally equiv-alent types.

  One is a type name that denotes the other.

If type names are treated as standing for themselves, then the first two condi-tions in the above definition lead to name equivalence of type expressions.

Name-equivalent expressions are assigned the same value number, if we use Algorithm 6.3. Structural equivalence can be tested using the unification algo-rithm in Section 6.5.5.

3. Declarations

We shall study types and declarations using a simplified grammar that declares just one name at a time; declarations with lists of names can be handled as discussed in Example 5.10. The grammar is

The fragment of the above grammar that deals with basic and array types was used to illustrate inherited attributes in Section 5.3.2. The difference in this section is that we consider storage layout as well as types.

Nonterminal D generates a sequence of declarations. Nonterminal T gen-erates basic, array, or record types. Nonterminal B generates one of the basic types int and float. Nonterminal C, for "component," generates strings of zero or more integers, each integer surrounded by brackets. An array type con-sists of a basic type specified by B, followed by array components specified by nonterminal C. A record type (the second production for T) is a sequence of declarations for the fields of the record, all surrounded by curly braces.

4. Storage Layout for Local Names

From the type of a name, we can determine the amount of storage that will be needed for the name at run time. At compile time, we can use these amounts to assign each name a relative address. The type and relative address are saved in the symbol-table entry for the name. Data of varying length, such as strings, or data whose size cannot be determined until run time, such as dynamic arrays, is handled by reserving a known fixed amount of storage for a pointer to the data. Run-time storage management is discussed in Chapter 7.

Address Alignment

The storage layout for data objects is strongly influenced by the address-ing constraints of the target machine. For example, instructions to add integers may expect integers to be aligned, that is, placed at certain posi-tions in memory such as an address divisible by 4. Although an array of ten characters needs only enough bytes to hold ten characters, a compiler may therefore allocate 12 bytes — the next multiple of 4 — leaving 2 bytes unused. Space left unused due to alignment considerations is referred to as padding. When space is at a premium, a compiler may pack data so that no padding is left; additional instructions may then need to be executed at run time to position packed data so that it can be operated on as if it were properly aligned.

Suppose that storage comes in blocks of contiguous bytes, where a byte is the smallest unit of addressable memory. Typically, a byte is eight bits, and some number of bytes form a machine word. Multibyte objects are stored in consecutive bytes and given the address of the first byte.

The width of a type is the number of storage units needed for objects of that type. A basic type, such as a character, integer, or float, requires an integral number of bytes. For easy access, storage for aggregates such as arrays and classes is allocated in one contiguous block of bytes.⁴

The translation scheme (SDT) in Fig. 6.15 computes types and their widths for basic and array types; record types will be discussed in Section 6.3.6. The SDT uses synthesized attributes type and width for each nonterminal and two variables t and w to pass type and width information from a B node in a parse tree to the node for the production C —> e. In a syntax-directed definition, t and w would be inherited attributes for C.

The body of the T-production consists of nonterminal B, an action, and nonterminal C, which appears on the next line. The action between B and C sets t to B.type and w to B. width. If B —>• int then B.type is set to integer and B.width is set to 4, the width of an integer. Similarly, if B -+ float then B.type is float and B.width is 8, the width of a float.

The productions for C determine whether T generates a basic type or an array type. If C —>• e, then t becomes C.type and w becomes C. width.

Otherwise, C specifies an array component. The action for C —> [ n u m ] C1 forms C.type by applying the type constructor array to the operands num.value and C1.type. For instance, the result of applying array might be a tree structure such as Fig. 6.14.

The width of an array is obtained by multiplying the width of an element by the number of elements in the array. If addresses of consecutive integers differ by 4, then address calculations for an array of integers will include multiplications by 4. Such multiplications provide opportunities for optimization, so it is helpful for the front end to make them explicit. In this chapter, we ignore other machine dependencies such as the alignment of data objects on word boundaries.

Example 6.9 : The parse tree for the type i n t [2] [3] is shown by dotted lines in Fig. 6.16. The solid lines show how the type and width are passed from B, down the chain of C's through variables t and w, and then back up the chain as synthesized attributes type and width. The variables t and w are assigned the values of B.type and B.width, respectively, before the subtree with the C nodes is examined. The values of t and w are used at the node for C —> e to start the evaluation of the synthesized attributes up the chain of C nodes.

5. Sequences of Declarations

Languages such as C and Java allow all the declarations in a single procedure to be processed as a group. The declarations may be distributed within a Java procedure, but they can still be processed when the procedure is analyzed. Therefore, we can use a variable, say offset, to keep track of the next available relative address.

The translation scheme of Fig. 6.17 deals with a sequence of declarations of the form T id, where T generates a type as in Fig. 6.15. Before the first declaration is considered, offset is set to 0. As each new name x is seen, x is entered into the symbol table with its relative address set to the current value of offset, which is then incremented by the width       of the type of x.

The semantic action within the production D —> T id ;         D1 creates a symboltable  entry  by      executing    top.put(id.lexeme,          T.type,        offset).        Here  top  denotes the current symbol table. The method top.put creates a symbol-table entry for id.lexeme, with type T.type and relative address offset in its data area.

The initialization of offset in Fig. 6.17 is more evident if the first production appears on one line as:

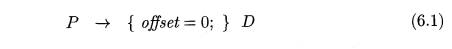
Nonterminals generating e, called marker nonterminals, can be used to rewrite productions so that all actions appear at the ends of right sides; see Sec-tion 5.5.4. Using a marker nonterminal M, (6.1) can be restated as:

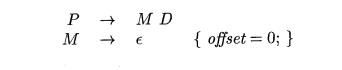
3. Fields in Records and Classes

The translation of declarations in Fig. 6.17 carries over to fields in records and classes. Record types can be added to the grammar in Fig. 6.15 by adding the following production

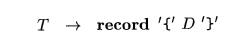
The fields in this record type are specified by the sequence of declarations generated by D. The approach of Fig. 6.17 can be used to determine the types and relative addresses of fields, provided we are careful about two things:

  The field names within a record must be distinct; that is, a name may appear at most once in the declarations generated by D.

  The offset or relative address for a field name is relative to the data area for that record.

Example 6.10:      The  use  of a name  x  for  a field within  a record does  not conflict with other uses of the name outside the record.  Thus, the three uses of x in the following declarations are distinct and do not  conflict with each other:

float x ;

record  { float  x; float  y; } p;

record  { int tag ;float x; float y; } q;

A subsequent assignment x = p. x + q. x; sets variable x to the sum of the fields named x in the records p and q. Note that the relative address of x in p differs from the relative address of x in q. •

For convenience, record types will encode both the types and relative ad-dresses of their fields, using a symbol table for the record type. A record type has the form record(t), where record is the type constructor, and i i s a symbol- table object that holds information about the fields of this record type.

The translation scheme in Fig. 6.18 consists of a single production to be added to the productions for T in Fig. 6.15. This production has two semantic actions. The embedded action before D saves the existing symbol table, denoted by top and sets top to a fresh symbol table. It also saves the current offset, and sets offset to 0. The declarations generated by D will result in types and relative addresses being put in the fresh symbol table. The action after D creates a record type using top, before restoring the saved symbol table and offset.

For concreteness, the actions in Fig. 6.18 give pseudocode for a specific im-plementation. Let class Env implement symbol tables. The call Env.push(top) pushes the current symbol table denoted by top onto a stack. Variable top is then set to a new symbol table. Similarly, offset is pushed onto a stack called Stack. Variable offset is then set to 0.

After the declarations in D have been translated, the symbol table top holds the types and relative addresses of the fields in this record. Further, offset gives the storage needed for all the fields. The second action sets T.type to record(top) and T. width to offset Variables top and offset are then restored to their pushed values to complete the translation of this record type.

This discussion of storage for record types carries over to classes, since no storage is reserved for methods. See Exercise 6.3.2.

7. Exercises for Section 6.3

Exercise 6 . 3 . 1 : Determine the types and relative addresses for the identifiers in the following sequence of declarations:

float  x;

record { float x;  float y;   } p;

record {  int tag;  float x;  float y;  } q;

Exercise 6.3.2 :     Extend the handling of field names in Fig. 6.18 to classes and single-inheritance class hierarchies.

Give an implementation of class Env that allows linked symbol tables, so that a subclass can either redefine a field name or refer directly to a field name in a superclass.

Give a translation scheme that allocates a contiguous data area for the fields in a class, including inherited fields. Inherited fields must maintain the relative addresses they were assigned in the layout for the superclass.