Translation of Expressions

Translation of Expressions

1 Operations Within Expressions

 2 Incremental Translation

 3 Addressing Array Elements

 4 Translation of Array References

 5 Exercises for Section 6.4

The rest of this chapter explores issues that arise during the translation of ex-pressions and statements. We begin in this section with the translation of ex-pressions into three-address code. An expression with more than one operator, like a + b* c, will translate into instructions with at most one operator per in-struction. An array reference A[i][j] will expand into a sequence of three-address instructions that calculate an address for the reference. We shall consider type checking of expressions in Section 6.5 and the use of boolean expressions to direct the flow of control through a program in Section 6.6.

1. Operations Within Expressions

The syntax-directed definition in Fig. 6.19 builds up the three-address code for an assignment statement S using attribute code for S and attributes addr and code for an expression E. Attributes S.code and E.code denote the three-address code for S and E, respectively. Attribute E.addr denotes the address that will hold the value of E. Recall from Section 6.2.1 that an address can be a name, a constant, or a compiler-generated temporary.

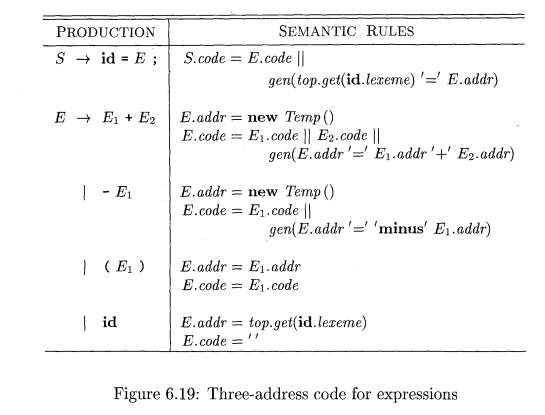
Consider the last production, E ->• id, in the syntax-directed definition in Fig. 6.19. When an expression is a single identifier, say x, then x itself holds the value of the expression. The semantic rules for this production define E.addr to point to the symbol-table entry for this instance of id. Let top denote the current symbol table. Function top. get retrieves the entry when it is applied to the string representation id.lexeme of this instance of id. E.code is set to the empty string.

When E —> (Ei), the translation of E is the same as that of the subex-pression Ei. Hence, E.addr equals Ei.addr, and E.code equals Ei.code.

The operators + and unary - in Fig. 6.19 are representative of the operators in a typical language. The semantic rules for E —> E1 + E2, generate code to compute the value of E from the values of E1 and E2. Values are computed into newly generated temporary names. If E1 is computed into Ei.addr and E2 into E2. addr, then E1 + E2 translates into t = E1. addr + E2. addr, where t is a new temporary name. E.addr is set to t. A sequence of distinct temporary names ti,t2,... is created by successively executing n e w Tempi).

For convenience, we use the notation gen(x '=' y '+' z) to represent the three-address instruction x = y + z. Expressions appearing in place of variables like x, y, and z are evaluated when passed to gen, and quoted strings like are taken literally.5 Other three-address instructions will be built up similarly 5 In syntax-directed definitions, gen builds an instruction and returns it.

In translation schemes, gen builds an instruction and incrementally emits it by putting it into the stream by applying gen to a combination of expressions and strings.

When we translate the production E -> Ei+E2, the semantic rules in Fig. 6.19 build up E.code by concatenating Ei.code, E2.code, and an instruction that adds the values of E1 and E2. The instruction puts the result of the addition into a new temporary name for E, denoted by E.addr.

The translation of E -» - E1 is similar. The rules create a new temporary for E and generate an instruction to perform the unary minus operation.

Finally, the production S id = E; generates instructions that assign the value of expression E to the identifier id. The semantic rule for this production uses function top.get to determine the address of the identifier represented by id, as in the rules for E —v id. S.code consists of the instructions to compute the value of E into an address given by E.addr, followed by an assignment to the address top.get(id.lexeme) for this instance of id.

Example 6.11 : The syntax-directed definition in Fig. 6.19 translates the as-signment statement a = b + - c; into the three-address code sequence

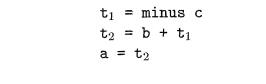
2. Incremental Translation

Code attributes can be long strings, so they are usually generated incremen-tally, as discussed in Section 5.5.2. Thus, instead of building up E.code as in Fig. 6.19, we can arrange to generate only the new three-address instructions, as in the translation scheme of Fig. 6.20. In the incremental approach, gen not only constructs a three-address instruction, it appends the instruction to the sequence of instructions generated so far. The sequence may either be retained in memory for further processing, or it may be output incrementally.

The translation scheme in Fig. 6.20 generates the same code as the syntax-directed definition in Fig. 6.19. With the incremental approach, the code at-tribute is not used, since there is a single sequence of instructions that is created by successive calls to gen. For example, the semantic rule for E ->• E1 + E₂ in Fig. 6.20 simply calls gen to generate an add instruction; the instructions to compute Ei into Ei.addr and E₂ into E₂.addr have already been generated.

The approach of Fig. 6.20 can also be used to build a syntax tree.  The new semantic action for          E -- > E1   + E2    creates a node by using a constructor,        as in  of generated instructions.

E  -- > Ei      + E2  {E.addr  =  new  Node(''+', E1.addr, E2.addr);   }

Here, attribute addr represents the address of a node rather than a variable or constant.

3. Addressing Array Elements

Array elements can be accessed quickly if they are stored in a block of consecu-tive locations. In C and Java, array elements are numbered 0 , 1 , . . . , n — 1, for an array with n elements. If the width of each array element is w, then the iih element of array A begins in location

where base is the relative address of the storage allocated for the array. That is, base is the relative address of A[0].

The formula (6.2) generalizes to two or more dimensions. In two dimensions, we write A[ii][i2] in C and Java for element i2 in row ii. Let w1 be the width of a row and let w2 be the width of an element in a row. The relative address of .A[zi][z2] can then be calculated by the formula

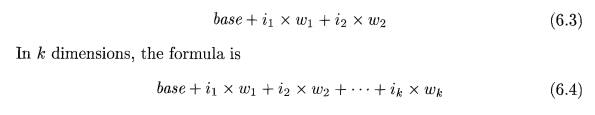
where Wj, for 1 =< j= < k, is the generalization of Wi and w2 in (6.3).

 Alternatively, the relative address of an array reference can be calculated in terms of the numbers of elements rij along dimension j of the array and the width w = Wk of a single element of the array. In two dimensions (i.e., k = 2 and w = w2), the location for A[n][i2 ] is given by

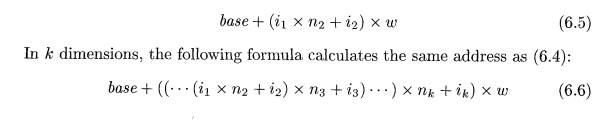
More generally, array elements need not be numbered starting at 0. In a one-dimensional array, the array elements are numbered low, low + 1 , . . . , high and base is the relative address of A[low}. Formula (6.2) for the address of A[i] is replaced by:

The expressions (6.2) and (6.7) can be both be rewritten as i x w + c, where the subexpression c = base — low x w can be precalculated at compile time.

Note that c = base when low is 0. We assume that c is saved in the symbol table entry for A, so the relative address of A[i] is obtained by simply adding i x w to c.

Compile-time precalculation can also be applied to address calculations for elements of multidimensional arrays; see Exercise 6.4.5. However, there is one situation where we cannot use compile-time precalculation: when the array's size is dynamic. If we do not know the values of low and high (or their gen-eralizations in many dimensions) at compile time, then we cannot compute constants such as c. Then, formulas like (6.7) must be evaluated as they are written, when the program executes.

The above address calculations are based on row-major layout for arrays, which is used in C and Java. A two-dimensional array is normally stored in one of two forms, either row-major (row-by-row) or column-major (column-by-column). Figure 6.21 shows the layout of a 2 x 3 array A in (a) row-major form and (b) column-major form. Column-major form is used in the Fortran family of languages.

We can generalize row- or column-major form to many dimensions. The generalization of row-major form is to store the elements in such a way that, as we scan down a block of storage, the rightmost subscripts appear to vary fastest, like the numbers on an odometer. Column-major form generalizes to the opposite arrangement, with the leftmost subscripts varying fastest.

4. Translation of Array References

The chief problem in generating code for array references is to relate the address-calculation formulas in Section 6.4.3 to a grammar for array references. Let nonterminal L generate an array name followed by a sequence of index expressions:

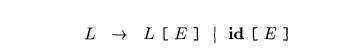
As in C and Java, assume that the lowest-numbered array element is 0.

Let us calculate addresses based on widths, using the formula (6.4), rather than on numbers of elements, as in (6.6). The translation scheme in Fig. 6.22 generates three-address code for expressions with array references. It consists of the productions and semantic actions from Fig. 6.20, together with productions involving nonterminal L.

Nonterminal L has three synthesized attributes:

1. L.addr denotes a temporary that is used while computing the offset for the array reference by summing the terms ij x Wj in (6.4).

   L.array is a pointer to the symbol-table entry for the array name. The base address of the array, say, L.array.base is used to determine the actual

/-value of an array reference after all the index expressions are analyzed.

   L.type is the type of the subarray generated by L. For any type t, we assume that its width is given by t.width. We use types as attributes, rather than widths, since types are needed anyway for type checking. For any array type t, suppose that t.elem gives the element type.

The production S -» id = E; represents an assignment to a nonarray vari-able, which is handled as usual. The semantic action for S —?> L = E; generates an indexed copy instruction to assign the value denoted by expression E to the location denoted by the array reference L. Recall that attribute L.array gives the symbol-table entry for the array. The array's base address — the address of its Oth element — is given by L.array.base. Attribute L.addr denotes the temporary that holds the offset for the array reference generated by L. The location for the array reference is therefore L.array.base[L.addr]. The generated instruction copies the r-value from address E.addr into the location for L.

Productions E -- > Ei+E₂ and E —> id are the same as before. The se-mantic action for the new production E —»• L generates code to copy the value from the location denoted by L into a new temporary. This location is L.array.base[L.addr], as discussed above for the production S -¥ L = E;. Again, attribute L.array gives the array name, and L.array.base gives its base address. Attribute L.addr denotes the temporary that holds the offset. The code for the array reference places the r-value at the location designated by the base and Example 6.12 : Let a denote a 2 x 3 array of integers, and let c, i, and j all denote integers. Then, the type of a is array(2, array(S, integer)). Its width w is 24, assuming that the width of an integer is 4. The type of a [ i ] is array(3, integer), of width w1 = 12. The type of a [ i ] [ j ] is integer.

An annotated parse tree for the expression c + a [ i ] [ j ] is shown in Fig. 6.23.

The expression is translated into the sequence of three-address instructions in Fig. 6.24. As usual, we have used the name of each identifier to refer to its symbol-table entry. •

5. Exercises for Section 6.4

Exercise 6 . 4 . 1 : Add to the translation of Fig.  6.19 rules for the following

productions:

a)  E     -+ Ei      *        E₂.

b)  E     ->•        +  Ei (unary plus).

Exercise 6 . 4 . 2 :  Repeat Exercise 6.4.1 for the incremental translation of Fig. 6.20.

E x e r c i se 6 . 4 . 3:   Use the  translation of Fig.  6.22  to translate the following

assignments:

a)  x  =  a [ i ]   +  b [ j ] .

b)  x  =  a [ i ] [ j ]      +  b [ i ] [ j ] .

! c)  x  =  a [ b [ i ] [ j ] ] [ c [ k ] ] .

Exercise 6 . 4 . 4 :  Revise the translation of Fig. 6.22 for array references of the

Fortran  style,  that  is,    1d[Ei,E₂,...         , E_n]   for  an  n-dimensional  array.

Exercise 6 . 4 . 5 : Generalize formula (6.7) to multidimensional arrays, and in-dicate what values can be stored in the symbol table and used to compute offsets. Consider the following cases:

a) An array A of two dimensions, in row-major form. The first dimension has indexes running from l1 to hi, and the second dimension has indexes from l₂ to h₂. The width of a single array element is w.

Symbolic Type Widths

The intermediate code should be relatively independent of the target ma-chine, so the optimizer does not have to change much if the code generator is replaced by one for a different machine. However, as we have described the calculation of type widths, an assumption regarding how basic types is built into the translation scheme. For instance, Example 6.12 assumes that each element of an integer array takes four bytes. Some intermediate codes, e.g., P-code for Pascal, leave it to the code generator to fill in the size of array elements, so the intermediate code is independent of the size of a machine word. We could have done the same in our translation scheme if we replaced 4 (as the width of an integer) by a symbolic constant.

b) The same as (a), but with the array stored in column-major form.

 c) An array A of k dimensions, stored in row-major form, with elements of size w. The jth. dimension has indexes running from lj to hj.

 d)  The same as (c) but with the array stored in column-major form.

E x e r c i se 6 . 4 . 6 : An integer array A[i, j] has index i ranging from 1 to 10 and index j ranging from 1 to 20. Integers take 4 bytes each. Suppose array A is stored starting at byte 0. Find the location of:

a)  A[4,5]            b)A[10,8]  c) A[3,17].

Exercise 6 . 4 . 7:  Repeat Exercise 6.4.6 if A is stored in column-major order.

Exercise 6 . 4 . 8: A real array A[i,j, k] has index i ranging from 1 to 4, index j ranging from 0 to 4, and index k ranging from 5 to 10. Reals take 8 bytes each. Suppose array A is stored starting at byte 0. Find the location of:

a)  A[3,4,5]            b)A[l,2,7]         c) A[4,3,9].

Exercise 6 . 4 . 9 :  Repeat Exercise 6.4.8 if A is stored in column-major order.