Units for Expressing Concentration

Units for Expressing Concentration

Concentration is a general measurement unit stating the amount of solute present in a known amount of solution

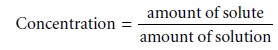
Although the terms “solute” and “solution” are often associated with liquid sam- ples, they can be extended to gas-phase and solid-phase samples as well. The actual units for reporting concentration depend on how the amounts of solute and solu- tion are measured. Table 2.4 lists the most common units of concentration.

Molarity and Formality

Both molarity and formality express concentration as moles of solute per liter of solu- tion. There is, however, a subtle difference between molarity and formality. Molarity is the concentration of a particular chemical species in solution. Formality, on the other hand, is a substance’s total concentration in solution without regard to its spe- cific chemical form. There is no difference between a substance’s molarity and for- mality if it dissolves without dissociating into ions. The molar concentration of a so- lution of glucose, for example, is the same as its formality.

For substances that ionize in solution, such as NaCl, molarity and formality are different. For example, dissolving 0.1 mol of NaCl in 1 L of water gives a solution containing 0.1 mol of Na+ and 0.1 mol of Cl–. The molarity of NaCl, therefore, is zero since there is essentially no undissociated NaCl in solution. 

The solution, instead, is 0.1 M in Na+ and 0.1 M in Cl–. The formality of NaCl, however, is 0.1 F because it represents the total amount of NaCl in solution. The rigorous definition of molarity, for better or worse, is largely ignored in the current literature, as it is in this text. When we state that a solution is 0.1 M NaCl we understand it to consist of Na+ and Cl– ions. The unit of formality is used only when it provides a clearer de- scription of solution chemistry.

Molar concentrations are used so frequently that a symbolic notation is often used to simplify its expression in equations and writing. The use of square brackets around a species indicates that we are referring to that species’ molar concentration. Thus, [Na+] is read as the “molar concentration of sodium ions.”

Normality

Normality is an older unit of concentration that, although once commonly used, is frequently ignored in today’s laboratories. Normality is still used in some hand- books of analytical methods, and, for this reason, it is helpful to understand its meaning. For example, normality is the concentration unit used in Standard Meth- ods for the Examination of Water and Wastewater,1 a commonly used source of ana- lytical methods for environmental laboratories.

Normality makes use of the chemical equivalent, which is the amount of one chemical species reacting stoichiometrically with another chemical species. Note that this definition makes an equivalent, and thus normality, a function of the chemical reaction in which the species participates. Although a solution of H₂SO₄ has a fixed molarity, its normality depends on how it reacts.

The number of equivalents, n, is based on a reaction unit, which is that part of a chemical species involved in a reaction. In a precipitation reaction, for example, the reaction unit is the charge of the cation or anion involved in the reaction; thus for the reaction

n = 2 for Pb2+ and n = 1 for I–. In an acid–base reaction, the reaction unit is the number of H+ ions donated by an acid or accepted by a base. For the reaction be- tween sulfuric acid and ammonia

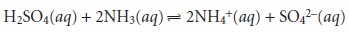
we find that n = 2 for H₂SO₄ and n = 1 for NH₃. For a complexation reaction, the reaction unit is the number of electron pairs that can be accepted by the metal or donated by the ligand. In the reaction between Ag+ and NH₃

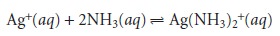
the value of n for Ag+ is 2 and that for NH₃ is 1. Finally, in an oxidation–reduction reaction the reaction unit is the number of electrons released by the reducing agent or accepted by the oxidizing agent; thus, for the reaction

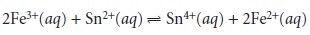
n = 1 for Fe3+ and n = 2 for Sn2+. Clearly, determining the number of equivalents for a chemical species requires an understanding of how it reacts.

Normality is the number of equivalent weights (EW) per unit volume and, like formality, is independent of speciation. An equivalent weight is defined as the ratio of a chemical species’ formula weight (FW) to the number of its equivalents

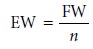
Consequently, the following simple relationship exists between normality and molarity.

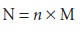
Example 2.1 illustrates the relationship among chemical reactivity, equivalent weight, and normality.

Molality

Molality is used in thermodynamic calculations where a temperature independent unit of concentration is needed. Molarity, formality and normality are based on the volume of solution in which the solute is dissolved. Since density is a temperature de- pendent property a solution’s volume, and thus its molar, formal and normal concen- trations, will change as a function of its temperature. By using the solvent’s mass in place of its volume, the resulting concentration becomes independent of temperature.

Weight, Volume, and Weight-to-Volume Ratios

Weight percent (% w/w), volume percent (% v/v) and weight-to-volume percent (% w/v) express concentration as units of solute per 100 units of sample. A solution in which a solute has a concentration of 23% w/v contains 23 g of solute per 100 mL of solution.

Parts per million (ppm) and parts per billion (ppb) are mass ratios of grams of solute to one million or one billion grams of sample, respectively. For example, a steel that is 450 ppm in Mn contains 450 μg of Mn for every gram of steel. If we approxi- mate the density of an aqueous solution as 1.00 g/mL, then solution concentrations can be expressed in parts per million or parts per billion using the following relationships.

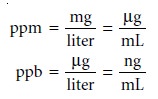
For gases a part per million usually is a volume ratio. Thus, a helium concentration of 6.3 ppm means that one liter of air contains 6.3 μL of He.

Converting Between Concentration Units

The units of concentration most frequently encountered in analytical chemistry are molarity, weight percent, volume percent, weight-to-volume percent, parts per mil- lion, and parts per billion. By recognizing the general definition of concentration given in equation 2.1, it is easy to convert between concentration units.

p-Functions

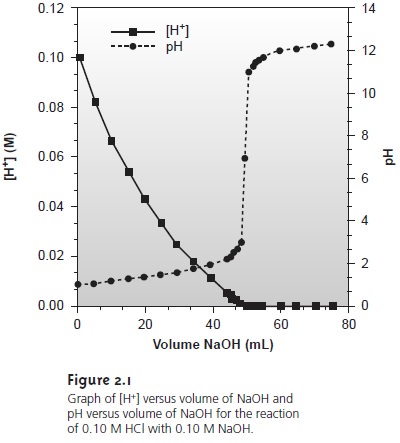
Sometimes it is inconvenient to use the concentration units in Table 2.4. For exam- ple, during a reaction a reactant’s concentration may change by many orders of mag- nitude. If we are interested in viewing the progress of the reaction graphically, we might wish to plot the reactant’s concentration as a function of time or as a function of the volume of a reagent being added to the reaction. Such is the case in Figure 2.1, where the molar concentration of H+ is plotted (y-axis on left side of figure) as a function of the volume of NaOH added to a solution of HCl. The initial [H+] is 0.10 M, and its concentration after adding 75 mL of NaOH is 5.0 x 10–13 M. We can easily follow changes in the [H+] over the first 14 additions of NaOH. For the last ten addi- tions of NaOH, however, changes in the [H+] are too small to be seen.

When working with concentrations that span many orders of magnitude, it is often more convenient to express the concentration as a p-function. The p-func- tion of a number X is written as pX and is defined as

pX = –log(X)

Thus, the pH of a solution that is 0.10 M H+ is

pH = –log[H+] = –log(0.10) = 1.00

and the pH of 5.0 x 10–13 M H+ is

pH = –log[H+] = –log(5.0 x 10–13) = 12.30

Figure 2.1 shows how plotting pH in place of [H+] provides more detail about how the concentration of H+ changes following the addition of NaOH.