Numbers in Analytical Chemistry

Numbers in Analytical Chemistry

Analytical chemistry is inherently a quantitative science. Whether determining the concentration of a species in a solution, evaluating an equilibrium constant, mea- suring a reaction rate, or drawing a correlation between a compound’s structure and its reactivity, analytical chemists make measurements and perform calculations. In this section we briefly review several important topics involving the use of num- bers in analytical chemistry.

Fundamental Units of Measure

Imagine that you find the following instructions in a laboratory procedure: “Trans- fer 1.5 of your sample to a 100 volumetric flask, and dilute to volume.” How do you do this? Clearly these instructions are incomplete since the units of measurement are not stated. Compare this with a complete instruction: “Transfer 1.5 g of your sample to a 100-mL volumetric flask, and dilute to volume.” This is an instruction that you can easily follow.

Measurements usually consist of a unit and a number expressing the quantity of that unit. Unfortunately, many different units may be used to express the same physical measurement. For example, the mass of a sample weighing 1.5 g also may be expressed as 0.0033 lb or 0.053 oz. For consistency, and to avoid confusion, sci- entists use a common set of fundamental units, several of which are listed in Table 2.1. These units are called SI units after the Système International d’Unités. Other measurements are defined using these fundamental SI units. For example, we mea- sure the quantity of heat produced during a chemical reaction in joules, (J), where

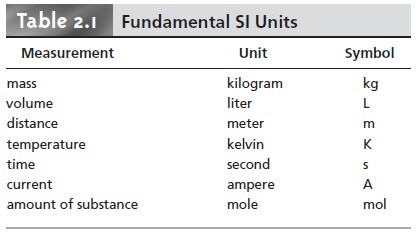
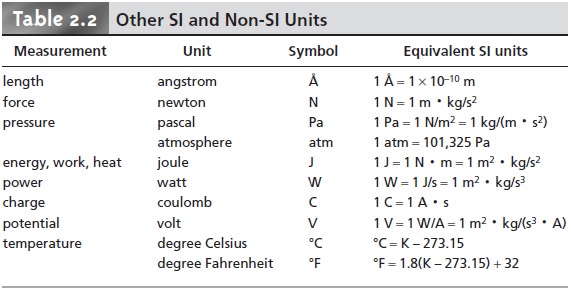
Table 2.2 provides a list of other important derived SI units, as well as a few com- monly used non-SI units.

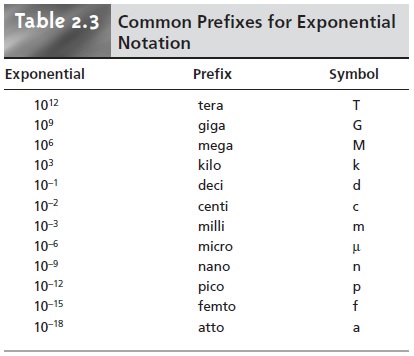
Chemists frequently work with measurements that are very large or very small. A mole, for example, contains 602,213,670,000,000,000,000,000 particles, and some analytical techniques can detect as little as 0.000000000000001 g of a compound. For simplicity, we express these measurements using scientific notation; thus, a mole contains 6.0221367 x 1023 particles, and the stated mass is 1 x 10–15 g. Some- times it is preferable to express measurements without the exponential term, replac- ing it with a prefix. A mass of 1 x 10–15 g is the same as 1 femtogram. Table 2.3 lists other common prefixes.

Significant Figures

Recording a measurement provides information about both its magnitude and un- certainty. For example, if we weigh a sample on a balance and record its mass as 1.2637 g, we assume that all digits, except the last, are known exactly. We assume that the last digit has an uncertainty of at least ±1, giving an absolute uncertainty of at least ±0.0001 g, or a relative uncertainty of at least

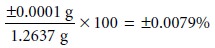
Significant figures are a reflection of a measurement’s uncertainty. The num- ber of significant figures is equal to the number of digits in the measurement, with the exception that a zero (0) used to fix the location of a decimal point is not con- sidered significant. This definition can be ambiguous. For example, how many sig- nificant figures are in the number 100? If measured to the nearest hundred, then there is one significant figure. If measured to the nearest ten, however, then two significant figures are included. To avoid ambiguity we use scientific notation. Thus, 1 x 102 has one significant figure, whereas 1.0 x 102 has two significant figures.

For measurements using logarithms, such as pH, the number of significant figures is equal to the number of digits to the right of the decimal, including all zeros. Digits to the left of the decimal are not included as significant figures since they only indicate the power of 10. A pH of 2.45, therefore, contains two signifi- cant figures.

Exact numbers, such as the stoichiometric coefficients in a chemical formula or reaction, and unit conversion factors, have an infinite number of significant figures. A mole of CaCl₂, for example, contains exactly two moles of chloride and one mole of calcium. In the equality

1000 mL = 1 L

both numbers have an infinite number of significant figures.

Recording a measurement to the correct number of significant figures is im- portant because it tells others about how precisely you made your measurement. For example, suppose you weigh an object on a balance capable of measuring mass to the nearest ±0.1 mg, but record its mass as 1.762 g instead of 1.7620 g. By failing to record the trailing zero, which is a significant figure, you suggest to others that the mass was determined using a balance capable of weighing to only the nearest ±1 mg. Similarly, a buret with scale markings every 0.1 mL can be read to the nearest ±0.01 mL. The digit in the hundredth’s place is the least sig- nificant figure since we must estimate its value. Reporting a volume of 12.241 mL implies that your buret’s scale is more precise than it actually is, with divi- sions every 0.01 mL.

Significant figures are also important because they guide us in reporting the re- sult of an analysis. When using a measurement in a calculation, the result of that calculation can never be more certain than that measurement’s uncertainty. Simply put, the result of an analysis can never be more certain than the least certain mea- surement included in the analysis.

As a general rule, mathematical operations involving addition and subtraction are carried out to the last digit that is significant for all numbers included in the cal- culation. Thus, the sum of 135.621, 0.33, and 21.2163 is 157.17 since the last digit that is significant for all three numbers is in the hundredth’s place.

135.621 + 0.33 + 21.2163 = 157.1673 = 157.17

When multiplying and dividing, the general rule is that the answer contains the same number of significant figures as that number in the calculation having the fewest significant figures. Thus,

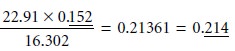
It is important to remember, however, that these rules are generalizations. What is conserved is not the number of significant figures, but absolute uncertainty when adding or subtracting, and relative uncertainty when multiplying or dividing. For example, the following calculation reports the answer to the correct number of significant figures, even though it violates the general rules outlined earlier.

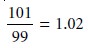
Since the relative uncertainty in both measurements is roughly 1% (101 ±1, 99 ±1), the relative uncertainty in the final answer also must be roughly 1%. Reporting the answer to only two significant figures (1.0), as required by the general rules, implies a relative uncertainty of 10%. The correct answer, with three significant figures, yields the expected relative uncertainty.

Finally, to avoid “round-off ” errors in calculations, it is a good idea to retain at least one extra significant figure throughout the calculation. Better yet, invest in a good scientific calculator that allows you to perform lengthy calculations without recording intermediate values. When the calculation is complete, the final answer can be rounded to the correct number of significant figures using the following simple rules.

·              Retain the least significant figure if it and the digits that follow are less than halfway to the next higher digit; thus,  rounding 12.442 to the nearest tenth gives 12.4 since 0.442 is less than halfway between 0.400 and 0.500.

·              Increase the least significant figure by 1 if it and the digits that follow are more than halfway to the next higher digit; thus, rounding 12.476 to the nearest tenth gives 12.5 since 0.476 is more than halfway between 0.400 and 0.500.

·              If the least significant figure and the digits that follow are exactly halfway to the next higher digit, then round the least significant figure to the nearest even number; thus, rounding 12.450 to the nearest tenth gives 12.4, but rounding 12.550 to the nearest tenth gives 12.6. Rounding in this manner prevents us from introducing a bias by always rounding up or down