Uniform Stress

Uniform Stress

If, in some orientation (x,y,z), shear stresses vanish throughout the body and the normal stresses are constant everywhere,

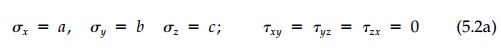
and all the field equations are satisfied. Strains are also constant giving the displacements by finite linear transformation as discussed in Chapter 1. If one stress is zero, the general case reduces to plane stress or, if say Ïƒ_y =v(σ_{x +} Ïƒ_z), there is uniform plane strain (E_{y =} 0).

Another common situation is the triaxial state where two of the stresses are equal, say:

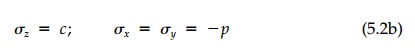
Unlike plane stress or plane strain, the triaxial field really is two-dimensional, in that, because the stresses are isotropic in the x-y plane, there is only one Mohr’s Circle throughout the body.

We create this situation in the laboratory in a triaxial cell by first pressurizing the sample in a chamber to some confining pressure, â€'p, and then increasing or decreasing the vertical stress with weights or with a hydraulic piston (Figure 5.1). This device is particularly useful for testing granular materials, which have little or no tensile strength. Both invariants can be controlled independently. A pure deviatoric test can be devised to determine the shear modulus, G, and

yield point. For example, the confining pressure can be decreased while the vertical stress is increased such that the radius of Mohr’s Circle grows while the mean stress remains constant. Conversely, we can determine the bulk modulus, K, by keeping Ïƒ_{z =-}  p throughout the test. A uniaxial state of uniform stress is achieved corresponding to an unconfined compression test if p = 0.

Depending on the boundary conditions and material properties, all of these uniform stress fields can occur in the half-space loaded by a constant surface load, q (Figure 5.2). Because of the semi-infinite geometric condition, there can be no shear strains and E_x = E_y = 0. Therefore

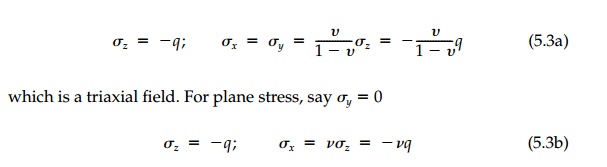
If v = 0, then the solution reduces to a simple uniaxial field of unconfined compression or if v=0.5 .5 (incompressible), it becomes the isotropic field of hydrostatic compression (σ_x = Ïƒ_y = Ïƒ_z =- q).