Pure Bending of Plates

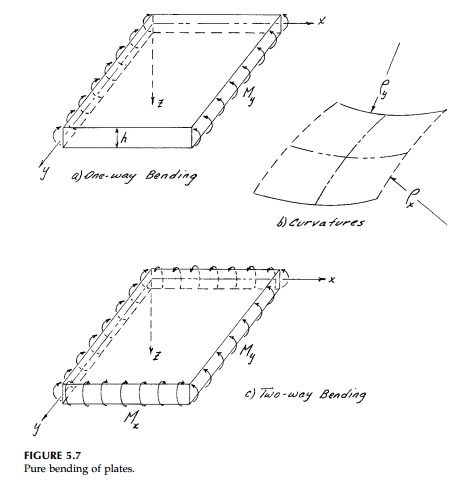
Pure Bending of Plates

This result for pure, one-way bending can, by superposition, be used to gen-erate the solution for combined bending of prismatic beams where a moment, M_y , is applied in addition to M_z. The result from the previous sec-tion can also be used to derive a solution for pure bending of plates which, as for beams, is the starting point for the study of their flexural behavior under more complicated loading and support conditions.

First consider a plate of uniform thickness, h, in pure bending around only the y axis due to a uniformly distributed moment, M_y , per unit length. The top and bottom of the plate will become anticlastic surfaces as shown in Figure 5.7 with the curvature 1/ρ convex in the yz plane. The moment of inertia per unit length is I = h³/12 and therefore by the simple bending theory of the previews pages.

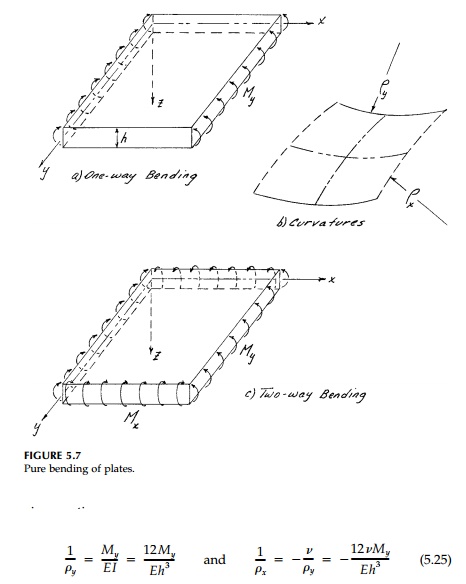
With distributed moments along both perpendicular edges (Figure 5.7c), the curvatures, stresses, and deflections can be found by superposition. With a bending moment per unit length around the x axis, M_x, as well as M_y

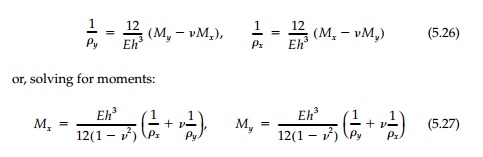
and the corresponding stresses are σ_{i =} M_iz/I.

The assumption of an anticlastic surface corresponds to the assumption that the vertical deflection is very small in comparison to the thickness. For this situation, we can use the approximation that the curvatures are given by the second derivatives of the deflection:

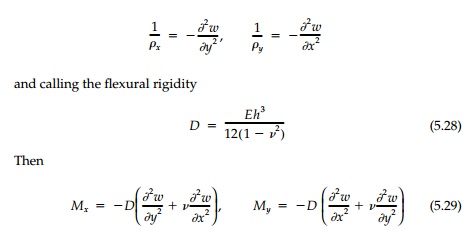
Two special cases are of particular note. To bend the plate into a cylindrical sur face, say one with the longitudinal direction parallel to the y axis

Usually the moments in plates are not constant, even away from the boundaries due to surface loads that introduce shears. However, just as for beams, these formulas for pure bending can be used with confidence away from stress-concentration points if the thickness is small compared to the width and length of the plate.