Geostatic Fields

Geostatic Fields

If, rather than surface traction, self weight is the loading, geostatic fields occur. We shall see in the next chapter that a general solution for arbitrary geometry is very difficult (actually unknown for some simple and important cases), but for the half-space and the uniaxial case, a solution is straightfor-ward.

Considering first the half-space where z is again taken as the depth coordinate, vertical equilibrium and the geometric condition that E_{x =E y}  = 0 everywhere lead to the solution:

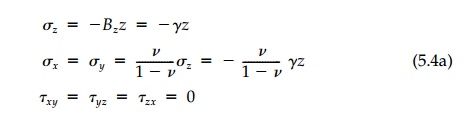
which, if v=1/₂ , is again isotropic. Since the only variable is z, the half-space can be considered of finite depth, H, supported on a rigid base as shown in Figure 5.3. The vertical displacement is therefore:

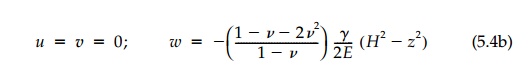
Determining the support condition necessary to achieve the linear geo-static stress field in the uniaxial case provides a simple demonstration of the physical importance of elastic rotations and the efficiency of determining them as a prelude to calculating the displacement field. Consider the block shown in Figure 5.4 standing under its own self weight and free now to

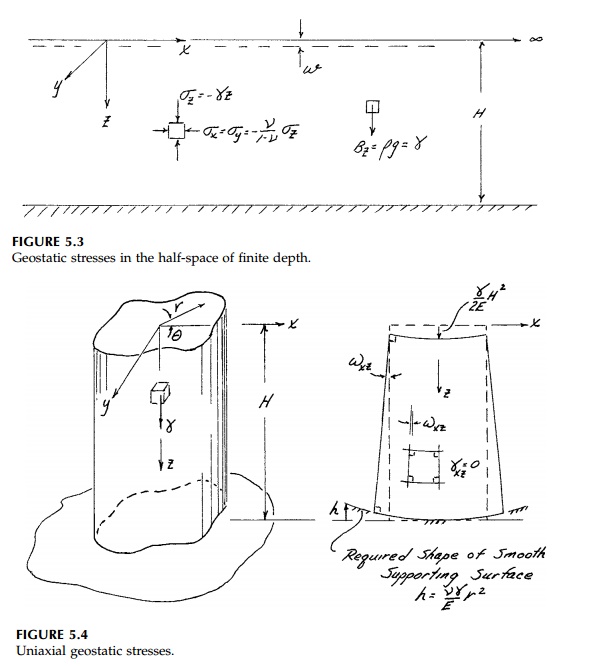
since from symmetry at x  = 0, Ï‰_{xz =} 0 and the integration constant is zero. Similarly following the same procedure,

Thus to achieve a uniform contact pressure, â€'γH, at z = H, the supporting surface (Figure 5.4) must be a smooth parabolic dish satisfying the displace-ment boundary condition dictated by the required vertical displacement. If, however, the supporting surface were flat, this geostatic solution, by St. Venant’s principle, would still be correct some distance from the bottom since the actual distribution of the contact stress must, by vertical equilibrium, be statically equivalent to a uniform distribution.