Linear Free Fields: Isotropic Stress

Linear Free Fields

The second-order, partial differential field equations in terms of stress [Equations (4.4)] can obviously be satisfied by constant or linear functions of position if body forces are also constant or linear functions. If the equilibrium equations are satis-fied, then such a constant or linear stress field is the correct solution to the prob-lem specified by the appropriate boundary conditions.

While such elementary solutions may appear trivial in a mathematical sense, they are extremely important in practice since they correspond to simple “strength-of-materials-type“ analysis on which the great majority of design deci-sions are based. Moreover, they are self-sustaining or “free fields“ that do not damp out by St. Venant’s Principle into some more uniform distribution.* Each stress component or combination of them, such as the invariants, can be visual-ized as a flat membrane, either level or tilted, which is stretched between a closed boundary. They are, therefore, harmonic functions satisfying the Laplace equa-tion. To achieve this condition, the boundary traction obviously must be constant or linear on shapes dictated by the membrane of constant slope.

Isotropic Stress

Consider first the most basic stress field in three dimensions:

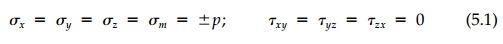
Everywhere Mohr’s Circle is a point and all directions are principal (i.e., the mem-brane is flat at the elevation, p, above any cross-section). The boundary surface must also be loaded with uniform tension (vacuum) or compression (hydrostatic pressure). The normal strains are also isotropic and equal p/3K. Since there are no deviatoric stress components or elastic rotations, the displacements are a lin-ear function of the distance from the origin, the location of which is arbitrary.