Uniform Acceleration of the Half space

Uniform Acceleration of the Half-space

With a horizontal component of body force, the behavior of the half-space is quite different. Although such body forces may arise in many ways (seepage being a common source in soils), acceleration, as for example in an earth-quake, is probably the most important.

Consider the half-space of finite depth H of material with unit weight Î³. From the previous section, the geostatic field is:

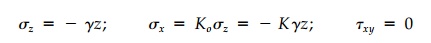
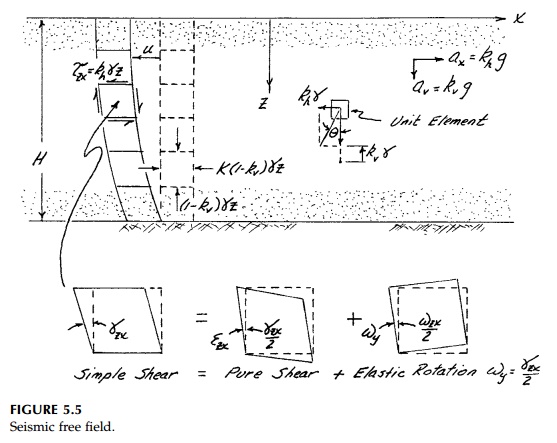
If uniform horizontal* and vertical accelerations, a_x and a_z, are now applied to the layer as in Figure 5.5, and the two-dimensional differential equations of equilibrium become:

and the field can be thought of as “one-dimensional plane strain“ (i.e., Ïƒ _{x =} Ïƒ _y and nothing can be a function of x or y). Thus, with the free-surface boundary condition at z =0, Equations (5.10) can be integrated directly to give the solution:

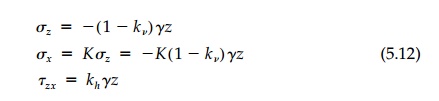
Essentially this dynamic (actually pseudostatic) solution for the free field is the geostatic free field with a unit weight of (1 â€' k_v)γ superimposed with shear

introduced by the horizontal acceleration component. However, considering the deformation, this is not “pure shear,“ but a case of “simple shear“ since there must be an elastic rotation field that keeps horizontal planes from rotating. From Equation (4.13) or by inspection

This simple result is remarkable. Both the geometric field condition  E_x = E_y = 0 (nothing is a function of x or y) and the equilibrium equations hold no matter what the distribution of acceleration or material properties. There is really no restriction on the distribution of k_h with depth, and assuming it constant is for convenience, not necessity. Moreover, the equations and their solution for the stress field must apply throughout the acceleration pulse past yield in the plas-tic range to eventual failure, which can only occur by base sliding. This exact solution does require that, if there are finite lateral boundaries, then the bound-ary traction on them and their displacement be distributed as the field equa-tions dictate. However, by St. Venant’s principle, perturbations to the free field will be insignificant away from the lateral boundaries as long as the resultant lateral force is equivalent. We will return to the seismic postyield behavior in later chapters on plasticity and limit analysis.