Two Simple Hash Functions

TWO SIMPLE HASH FUNCTIONS

To get some feel for the security considerations involved in cryptographic hash functions, we present two simple, insecure hash functions in this section. All hash functions operate using the following general principles. The input (message, file, etc.) is viewed as a sequence of n-bit blocks. The input is processed one block at a time in an iterative fashion to produce an n-bit hash function.

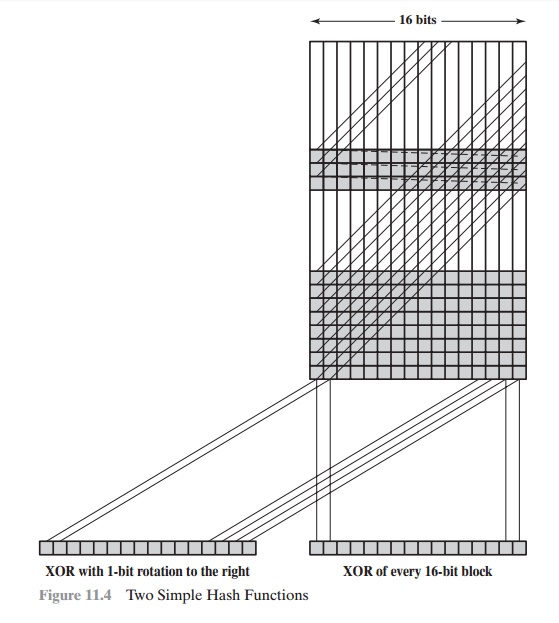
One of the simplest hash functions is the bit-by-bit exclusive-OR (XOR) of every block. This can be expressed as

This operation produces a simple parity for each bit position and is known as    a longitudinal redundancy check. It is reasonably effective for random data as a    data integrity check. Each  n-bit hash value is equally likely. Thus, the probability  that a data error will result in an unchanged hash value is 2-n. With more predictably formatted data, the function is less effective. For example, in most normal text files, the high-order bit of each octet is always zero. So if a 128-bit   hash value is used, instead of an effectiveness of 2-128, the hash function on this    type of data has an effectiveness of    2-112.

A simple way to improve matters is to perform a one-bit circular shift, or rota- tion, on the hash value after each block is processed. The procedure can be summa- rized as follows.

1.                                    Initially set the n-bit hash value to zero.

2.                                    Process each successive n-bit block of data as follows:

a.                                          Rotate the current hash value to the left by one bit.

b.                                          XOR the block into the hash value.

This has the effect of “randomizing” the input more completely and overcoming any regularities that appear in the input. Figure 11.4 illustrates these two types of hash functions for 16-bit hash values.

Although the second procedure provides a good measure of data integrity, it is virtually useless for data security when an encrypted hash code is used with a plaintext

message, as in Figures 11.2b and 11.3a. Given a message, it is an easy matter to produce a new message that yields that hash code: Simply prepare the desired alternate message and then append an n-bit block that forces the new message plus block to yield the desired hash code.

Although a simple XOR or rotated XOR (RXOR) is insufficient if only the hash code is encrypted, you may still feel that such a simple function could be useful when the message together with the hash code is encrypted (Figure 11.2a). But you must be careful. A technique originally proposed by the National Bureau of Standards used the simple XOR applied to 64-bit blocks of the  message and then an encryption of the entire message that used the cipher block chaining (CBC) mode. We can define the scheme as follows: Given a message M consisting of a sequence of 64-bit blocks X1, X2, Á , XN, define the hash code h  =      H(M) as

the block-by-block XOR of all blocks and append the hash code as the   final

block:

h = XN+1  = X1 Ⓧ X2 Ⓧ Á Ⓧ XN

Next, encrypt the entire message plus hash code using CBC mode to produce the encrypted message Y1, Y2, ..... , YN+1. [JUEN85] points out several ways in which the ciphertext of this message can be manipulated in such a way that it is not detectable by the hash code. For example, by the definition of CBC (Figure 6.4), we have

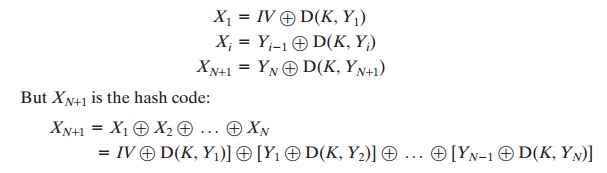
Because the terms in the preceding equation can be XORed in any order, it follows that the hash code would not change if the ciphertext blocks were permuted.