Hash Functions Based on Cipher Block Chaining

HASH FUNCTIONS BASED ON CIPHER BLOCK CHAINING

A number of proposals have been made for hash functions based on using a cipher block chaining technique, but without using the secret key. One of the first such proposals was that of Rabin [RABI78]. Divide a message M into fixed-size blocks M1, M2, Á , MN and use a symmetric encryption system such as DES to compute the hash code G as

This is similar to the CBC technique, but in this case, there is no secret key. As with any hash code, this scheme is subject to the birthday attack, and if the encryption algorithm is DES and only a 64-bit hash code is produced, then the system is vulnerable.

Furthermore, another version of the birthday attack can be used even if the opponent has access to only one message and its valid signature and cannot obtain multiple signings. Here is the scenario: We assume that the opponent intercepts a message with a signature in the form of an encrypted hash code and that the unencrypted hash code is m bits long.

1.                                    Use the algorithm defined at the beginning of this subsection to calculate the unencrypted hash code G.

2.                                    Construct any desired message in the form Q1, Q2, ………, QN - 2.

3.                                    Compute Hi = E(Qi, Hi - 1) for 1 … i … (N - 2).

4.                                    Generate 2m/2 random blocks; for each block X, compute E(X, HN - 2). Generate an additional 2m/2 random blocks; for each block Y, compute D(Y, G), where D is the decryption function corresponding to E.

5.                                    Based on the birthday paradox, with high probability there will be an X and  Y

such that E(X, HN - 2) = D(Y, G).

6.                                    Form the message Q1, Q2, Á , QN - 2, X, Y. This message has the hash code G

and therefore can be used with the intercepted encrypted signature.

This form of attack is known as a meet-in-the-middle-attack. A number  of researchers have proposed refinements intended to strengthen  the  basic  block chaining approach. For example, Davies and Price [DAVI89] describe the variation:

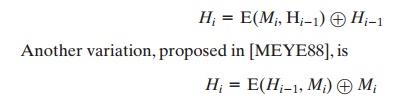
However, both of these schemes have been shown to be vulnerable to a variety of attacks [MIYA90]. More generally, it can be shown that some form of birthday attack will succeed against any hash scheme involving the use of cipher block chain- ing without a secret key, provided that either the resulting hash code is small enough (e.g., 64 bits or less) or that a larger hash code can be decomposed into independent subcodes [JUEN87].

Thus, attention has been directed at finding other approaches to   hashing.

Many of these have also been shown to have weaknesses [MITC92].