Requirements and Security

REQUIREMENTS AND SECURITY

Before proceeding, we need to define two terms. For a hash value h = H(x), we say that x is the preimage of h. That is, x is a data block whose hash function, using the function H, is h. Because H is a many-to-one mapping, for any given hash value h, there will in general be multiple preimages. A collision occurs if we have x != y and H(x) = H(y). Because we are using hash functions for data integrity, collisions are clearly undesirable.

Let us consider how many preimages are there for a given hash value, which is a measure of the number of potential collisions for a given hash value. Suppose the length of the hash code is n bits, and the function H takes as input messages or data blocks of length b bits with b 7 n. Then, the total number of possible messages is 2b and the total number of possible hash values is 2n. On average, each hash value corresponds to 2b/n preimages. If H tends to uniformly distribute hash values then, in fact, each hash value will have close to 2b/n preimages. If we now allow inputs of arbitrary length, not just a fixed length of some number of bits, then the number of preimages per hash value is arbitrarily large. However, the security risks in the use of a hash function are not as severe as they might appear from this analysis.   To understand better the security implications of cryptographic hash functions, we need precisely define their security requirements.

Security Requirements for Cryptographic Hash Functions

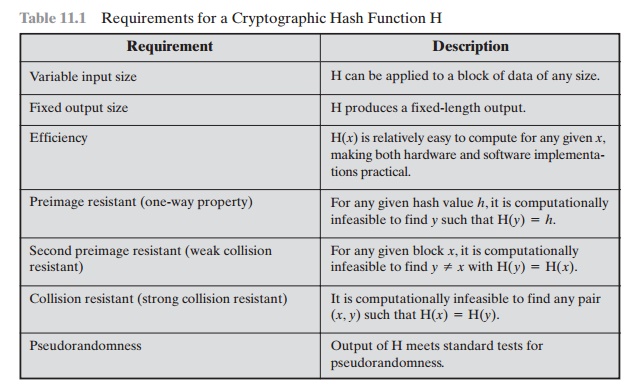
Table 11.1 lists the generally accepted requirements for a cryptographic hash function. The first three properties are requirements for the practical application of a hash function.

The fourth property, preimage resistant, is the one-way property: it is easy to generate a code given a message, but virtually impossible to generate a message given a code. This property is important if the authentication technique involves the use of a secret value (Figure 11.2c). The secret value itself is not sent. However, if the

Table 11.1 Requirements for a Cryptographic Hash Function H

hash function is not one way, an attacker can easily discover the secret value: If the attacker can observe or intercept a transmission, the attacker obtains the message    M, and the hash code h = H(S > M). The attacker then inverts the hash function to obtain S > M  =  H-1(MDM). Because the attacker now has both M and SAB >  M, it is   a trivial matter to recover   SAB.

The fifth property, second preimage resistant, guarantees that it is impossible to find an alternative message with the same hash value as a given message. This pre- vents forgery when an encrypted hash code is used (Figure 11.2b and Figure 11.3a). If this property were not true, an attacker would be capable of the following sequence: First, observe or intercept a message plus its encrypted hash code; second, generate an unencrypted hash code from the message; third, generate an alternate message with the same hash code.

A hash function that satisfies the first five properties in Table 11.1 is referred to as a weak hash function. If the sixth property, collision resistant, is also satisfied, then it is referred to as a strong hash function. A strong hash function protects against an attack in which one party generates a message for another party to sign. For example, suppose Bob writes an IOU message, sends it to Alice, and she signs it. Bob finds two messages with the same hash, one of which requires Alice to pay a small amount and one that requires a large payment. Alice signs the first message, and Bob is then able to claim that the second message is authentic.

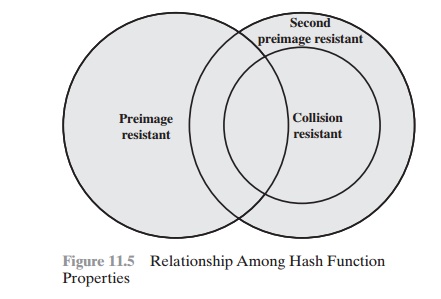
Figure 11.5 shows the relationships among the three resistant properties. A function that is collision resistant is also second preimage resistant, but the reverse is not necessarily true. A function can be collision resistant but not preimage resistant and vice versa. A function can be collision resistant but not second preimage resistant and vice versa. See [MENE97] for a discussion.

Table 11.2 shows the resistant properties required for various hash function applications.

The final requirement in Table 11.1, pseudorandomness, has not traditionally been listed as a requirement of cryptographic hash functions but is more or less implied. [JOHN05] points out that cryptographic hash functions are commonly used for key derivation and pseudorandom number generation, and that in message integrity applications, the three resistant properties depend on the output of the hash function appearing to be random. Thus, it makes sense to verify that in fact a given hash function produces pseudorandom output.

Brute-Force Attacks

As with encryption algorithms, there are two categories of attacks on hash functions: brute-force attacks and cryptanalysis. A brute-force attack does not depend on the specific algorithm but depends only on bit length. In the case of a hash function, a brute-force attack depends only on the bit length of the hash value. A cryptanalysis,  in contrast, is an attack based on weaknesses in a particular cryptographic algorithm. We  look first at brute-force attacks.

Table 11.2 Hash Function Resistance Properties Required for Various Data Integrity Applications

PREIMAGE AND SECOND PREIMAGE ATTACKS For a preimage or second preimage attack, an adversary wishes to find a value y such that H(y) is equal to a given hash value h. The brute-force method is to pick values of y at random and try each value until a collision occurs. For an m-bit hash value, the level of effort is proportional to 2m. Specifically, the adversary would have to try, on average, 2m - 1 values of y to find one that generates a given hash value h. This result is derived in Appendix 11A [Equation (11.1)].

COLLISION RESISTANT ATTACKS For a collision resistant attack, an adversary wishes to find two messages or data blocks, x and y, that yield the same hash function: H(x) = H(y). This turns out to require considerably less effort than a preimage or second preimage attack. The effort required is explained by a mathematical result referred to as the birthday paradox. In essence, if we choose random variables from a uniform distribution in the range 0 through N - 1, then the probability that a repeated element is encountered exceeds 0.5 after 1N choices have been made. Thus, for an m-bit hash value, if we pick data blocks at random, we can expect to find two data blocks with the same hash value within 22m = 2m/2 attempts. The mathematical derivation of this result is found in Appendix 11A.

Yuval proposed the following strategy to exploit the birthday paradox in a collision resistant attack [YUVA79].

1.                                    The source, A, is prepared to sign a legitimate message x by appending the appropriate m-bit hash code and encrypting that hash code with A’s private key (Figure 11.3a).

2.                                    The opponent generates 2m/2 variations x' of x, all of which convey essentially the same meaning, and stores the messages and their hash   values.

3.                                    The opponent prepares a fraudulent message y for which A’s signature is desired.

4.                                    The opponent generates minor variations y' of y, all of which convey essentially the  same  meaning. For  each  y', the  opponent  computes  H(y'), checks  for matches with any of the H(x') values, and continues until a match is found. That is, the process continues until a y¿ is generated with a hash value equal to the hash value of one of the x' values.

5.                                    The opponent offers the valid variation to A for signature. This signature can then be attached to the fraudulent variation for transmission to the intended recipient. Because the two variations have the same hash code, they will produce the same signature; the opponent is assured of success even though the encryption key is not known.

Thus, if a 64-bit hash code is used, the level of effort required is only on the order of 232 [see Appendix 11A, Equation (11.7)].

The generation of many variations that convey the same meaning is not difficult. For example, the opponent could insert a number of “space-space-backspace” character pairs between words throughout the document. Variations could then be generated by substituting “space-backspace-space” in selected instances. Alternatively, the

opponent could simply reword the message but retain the meaning. Figure 11.6 [DAVI89] provides an example.

To summarize, for a hash code of length m, the level of effort required, as we have seen, is proportional to the following.

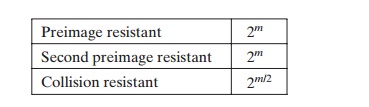
If collision resistance is required (and this is desirable for a general-purpose secure  hash  code), then  the  value 2m/2 determines  the  strength  of  the hash code against brute-force attacks. Van Oorschot and Wiener [VANO94] presented a design for a $10 million collision search machine for MD5, which has a 128-bit hash length, that could find a collision in 24 days. Thus, a 128-bit code may be viewed as inadequate. The next step up, if a hash code is treated as a sequence of 32 bits, is a 160-bit hash length. With a hash length of 160 bits, the same search machine would require over four thousand years to find a collision. With today’s technology, the  time would be much shorter, so that 160 bits now appears    suspect.

Cryptanalysis

As with encryption algorithms, cryptanalytic attacks on hash functions seek to exploit some property of the algorithm to perform some attack other than an exhaustive search. The way to measure the resistance of a hash algorithm to crypt- analysis is to compare its strength to the effort required for a brute-force attack. That is, an ideal hash algorithm will require a cryptanalytic effort greater than or equal to the brute-force effort.

In recent years, there has been considerable effort, and some successes, in devel- oping cryptanalytic attacks on hash functions. To understand these, we need to look at the overall structure of a typical secure hash function, indicated in Figure 11.7. This structure, referred to as an iterated hash function, was proposed by Merkle [MERK79, MERK89] and is the structure of most hash functions in use today, including SHA, which is discussed later in this chapter. The hash function takes an input message and partitions it into L fixed-sized blocks of b bits each. If necessary, the final block is padded to b bits. The final block also includes the value of the total length of the input to the hash function. The inclusion of the length makes the job of the opponent more difficult. Either the opponent must find two messages of equal length that hash to the same value or two messages of differing lengths that, together with their length values, hash to the same value.

The hash algorithm involves repeated use of a compression function, f, that takes two inputs (an n-bit input from the previous step, called the chaining variable, and a b-bit block) and produces an n-bit output. At the start of hashing, the chaining variable has an initial value that is specified as part of the algorithm. The final value

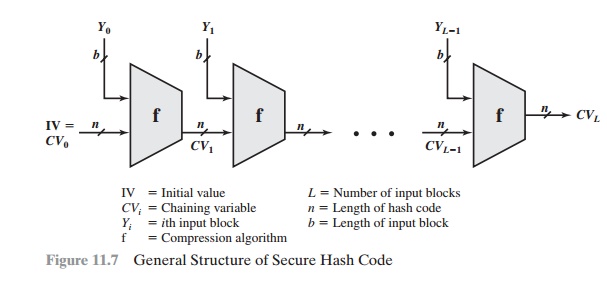
The motivation for this iterative structure stems from the observation by Merkle [MERK89] and Damgard [DAMG89] that if the compression function is collision resis- tant, then so is the resultant iterated hash function.1 Therefore, the structure can be used to produce a secure hash function to operate on a message of any length. The problem

of designing a secure hash function reduces to that of designing a collision-resistant compression function that operates on inputs of some fixed size.

Cryptanalysis of hash functions focuses on the internal structure of f and is based on attempts to find efficient techniques for producing collisions for a single execution of f. Once that is done, the attack must take into account the fixed value of

IV.      The attack on f depends on exploiting its internal structure. Typically, as with symmetric block ciphers, f consists of a series of rounds of processing, so that the attack involves analysis of the pattern of bit changes from round to round.

Keep in mind that for any hash function there must exist collisions, because we are mapping a message of length at least equal to twice the block size b (because we must append a length field) into a hash code of length n, where b >= n. What is required is that it is computationally infeasible to find collisions.

The attacks that have been mounted on hash functions are rather complex and beyond our scope here. For the interested reader, [DOBB96] and [BELL97] are recommended.