Secure Hash Algorithm (SHA)

SECURE HASH ALGORITHM (SHA)

In recent years, the most widely used hash function has been the Secure Hash Algorithm (SHA). Indeed, because virtually every other widely used hash function had been found to have substantial cryptanalytic weaknesses, SHA was more or less the last remaining standardized hash algorithm by 2005. SHA was devel- oped by the National Institute of Standards and Technology (NIST) and published as a federal information processing standard (FIPS 180) in 1993. When weak- nesses were discovered in SHA, now known as SHA-0, a revised version was issued as FIPS 180-1 in 1995 and is referred to as SHA-1. The actual standards document is entitled “Secure Hash Standard.” SHA is based on the hash function MD4, and its design closely models MD4. SHA-1 is also specified in RFC 3174, which essentially duplicates the material in FIPS 180-1 but adds a C code implementation.

SHA-1 produces a hash value of 160 bits. In 2002, NIST produced a revised version of the standard, FIPS 180-2, that defined three new versions of SHA, with hash value lengths of 256, 384, and 512 bits, known as SHA-256, SHA-384, and SHA-512, respectively. Collectively, these hash algorithms are known as SHA-2. These new versions have the same underlying structure and use the same types of modular arithmetic and logical binary operations as SHA-1. A revised document was issued as FIP PUB 180-3 in 2008, which added a 224-bit version (Table 11.3). SHA-2 is also specified in RFC 4634, which essentially duplicates the material in FIPS 180-3 but adds a C code implementation.

In 2005, NIST announced the intention to phase out approval of SHA-1 and move to a reliance on SHA-2 by 2010. Shortly thereafter, a research team described an attack in which two separate messages could be found that deliver the same SHA-1 hash using 269 operations, far fewer than the 280 operations previously thought needed to find a collision with an SHA-1 hash [WANG05]. This result should hasten the transition to SHA-2.

In this section, we provide a description of SHA-512. The other versions are quite similar.

SHA-512 Logic

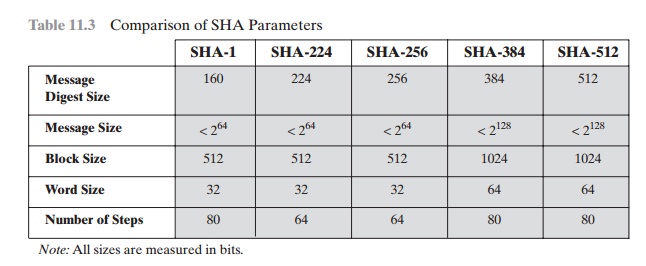
The algorithm takes as input a message with a maximum length of less than 2128 bits and produces as output a 512-bit message digest. The input is processed in 1024-bit blocks. Figure 11.8 depicts the overall processing of a message to produce a digest. This follows the general structure depicted in Figure 11.7. The processing consists of the following steps.

Table 11.3  Comparison of SHA Parameters

Step 1 Append padding bits. The message is padded so that its length is congruent to 896 modulo 1024 [length K 896(mod 1024)]. Padding is always added, even if the message is already of the desired length. Thus, the number of padding bits is in the range of 1 to 1024. The padding consists of a single 1 bit followed by the necessary number of 0  bits.

Step 2 Append length. A block of 128 bits is appended to the message. This block is treated as an unsigned 128-bit integer (most significant byte first) and contains the length of the original message (before the   padding).

The outcome of the first two steps yields a message that is an integer multiple of 1024 bits in length. In Figure 11.8, the expanded message is repre- sented as the sequence of 1024-bit blocks M1, M2, ….. , MN, so that the total length of the expanded message is N * 1024 bits.

Step 3 Initialize hash buffer. A 512-bit buffer is used to hold intermediate and final results of the hash function. The buffer can be represented as eight 64-bit reg- isters (a, b, c, d, e, f, g, h). These registers are initialized to the following 64-bit integers (hexadecimal values):

a = 6A09E667F3BCC908  e = 510E527FADE682D1 b = BB67AE8584CAA73B  f = 9B05688C2B3E6C1F c = 3C6EF372FE94F82B  g = 1F83D9ABFB41BD6B d = A54FF53A5F1D36F1  h = 5BE0CD19137E2179

These values are stored in big-endian format, which is the most significant byte of a word in the low-address (leftmost) byte position. These words were obtained by taking the first sixty-four bits of the fractional parts of the square roots of the first eight prime  numbers.

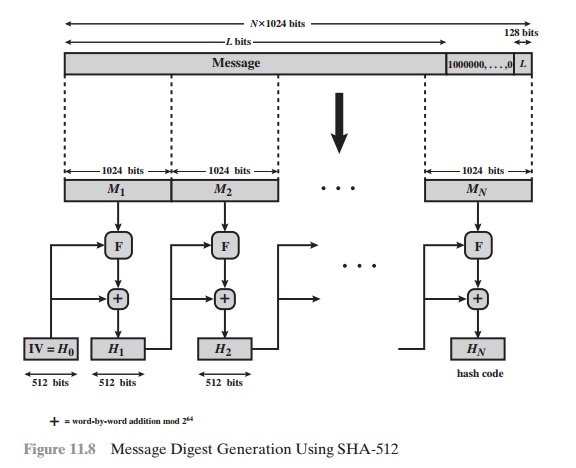
Step 4 Process message in 1024-bit (128-word) blocks. The heart of the algorithm is a module that consists of 80 rounds; this module is labeled F in Figure 11.8. The logic is illustrated in Figure 11.9.

Each round takes as input the 512-bit buffer value, abcdefgh, and updates the contents of the buffer. At input to the first round, the buffer has the value of the intermediate hash value, Hi - 1. Each round t makes use of a 64-bit value Wt, derived from the current 1024-bit block being processed (Mi). These values are derived using a message schedule described subsequently. Each round also makes use of an additive constant Kt, where 0 … t … 79 indicates one of the 80 rounds. These words represent the first 64 bits of the fractional parts of the cube roots of the first 80 prime numbers. 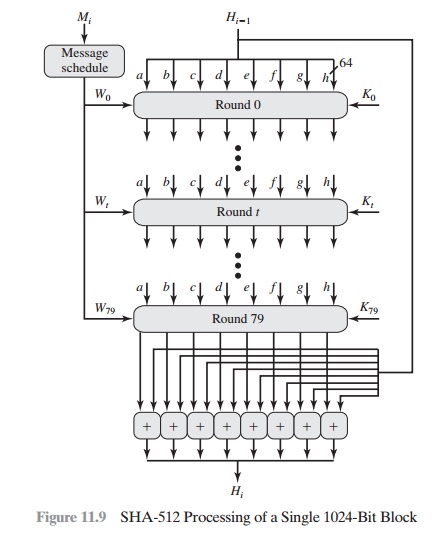The constants provide a “randomized” set of 64-bit patterns, which should eliminate any regularities in the input data. Table 11.4 shows these constants in hexadecimal format (from left to right).

The output of the eightieth round is added to the input to the first round (Hi - 1) to produce Hi. The addition is done independently for each of the eight

words in the buffer with each of the corresponding words in Hi - 1, using addi- tion modulo 264.

Step 5 Output. After all N 1024-bit blocks have been processed, the output from the Nth stage is the 512-bit message digest.

We can summarize the behavior of SHA-512 as follows:

SHA-512  Round Function

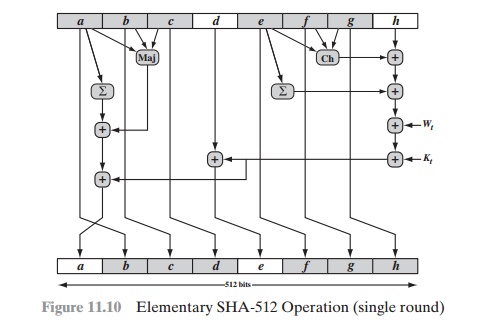
Let us look in more detail at the logic in each of the 80 steps of the processing of one 512-bit block (Figure 11.10). Each round is defined by the following set of equations:

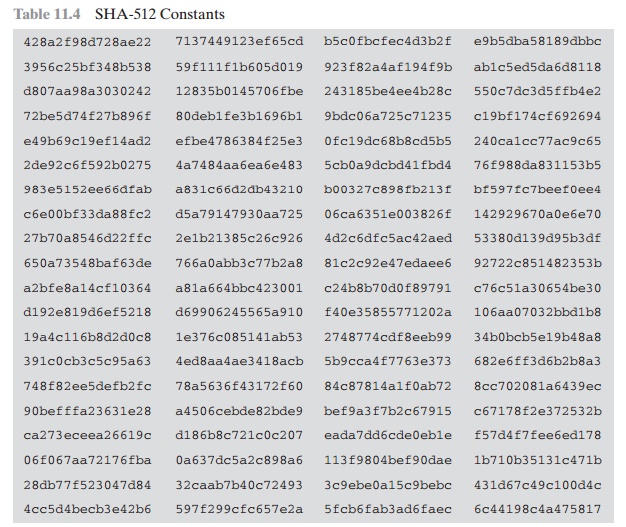
Two observations can be made about the round function.

1.                     Six of the eight words of the output of the round function involve simply per- mutation (b, c, d, f, g, h) by means of rotation. This is indicated by shading in Figure 11.10.

2.                     Only two of the output words (a, e) are generated by substitution. Word e is a function of input variables (d, e, f, g, h), as well as the round word Wt and the constant Kt. Word a is a function of all of the input variables except d, as well as the round word Wt and the constant Kt.

It remains to indicate how the 64-bit word values Wt are derived from the 1024-bit message. Figure 11.11 illustrates the mapping. The first 16 values of Wt are taken directly from the 16 words of the current block. The remaining values are defined as

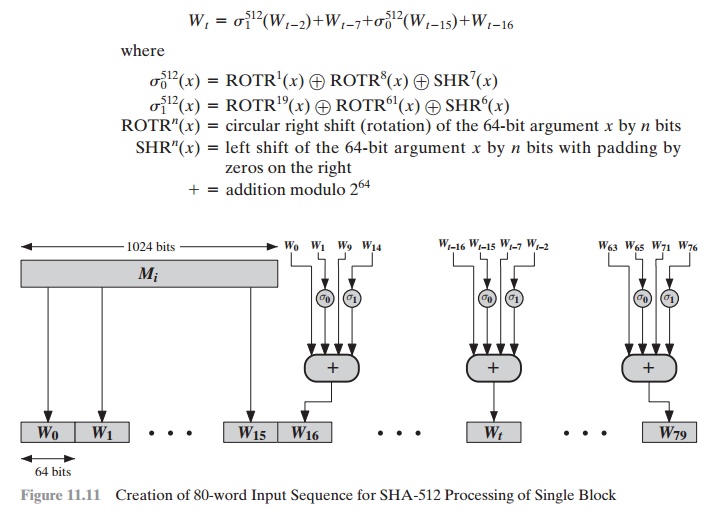
Thus, in the first 16 steps of processing, the value of Wt is equal to the corre- sponding word in the message block. For the remaining 64 steps, the value of Wt consists of the circular left shift by one bit of the XOR of four of the preceding values of Wt, with two of those values subjected to shift and rotate operations. This introduces a great deal of redundancy and interdependence into the message blocks that are compressed, which complicates the task of finding a different message block that maps to the same compression function output.

Figure 11.12 summarizes the SHA-512 logic.

The SHA-512 algorithm has the property that every bit of the hash code is a function of every bit of the input. The complex repetition of the basic function F produces results that are well mixed; that is, it is unlikely that two messages chosen at random, even if they exhibit similar regularities, will have the same hash code. Unless there is some hidden weakness in SHA-512, which has not so far been published, the difficulty of coming up with two messages having the same message digest is on the order of 2256 operations, while the difficulty of finding a message with a given digest is on the order of 2512 operations.

Example

We include here an example based on one in FIPS 180. We wish to hash a one-block message consisting of three ASCII characters: “abc”, which is equivalent to the fol- lowing 24-bit binary string:

01100001 01100010 01100011

Recall from step 1 of the SHA algorithm, that the message is padded to a length congruent to 896 modulo 1024. In this case of a single block, the padding consists of 896 - 24 = 872 bits, consisting of a “1” bit followed by 871 “0” bits. Then a 128-bit length value is appended to the message, which contains the length    of the original message (before the padding). The original length is 24 bits, or a hexadecimal value of 18. Putting this all together, the 1024-bit message block, in hexadecimal, is

This block is assigned to the words W0, Á ,W15 of the message schedule, which appears as follows.

As indicated in Figure 11.12, the eight 64-bit variables, a through h, are initial- ized to values H0,0 through H0,7. The following table shows the initial values of these variables and their values after each of the first two rounds.

Note that in each of the rounds, six of the variables are copied directly from variables from the preceding round.

The process continues through 80 rounds. The output of the final round is

73a54f399fa4b1b2 10d9c4c4295599f6 d67806db8b148677 654ef9abec389ca9 d08446aa79693ed7 9bb4d39778c07f9e 25c96a7768fb2aa3 ceb9fc3691ce8326

The hash value is then calculated as

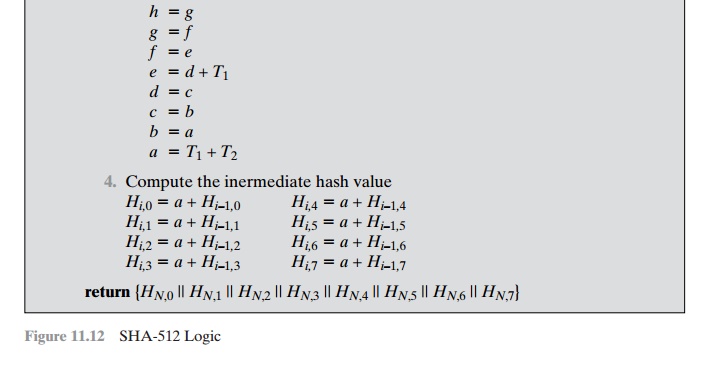
Suppose now that we change the input message by one bit, from “abc” to “cbc”. Then, the 1024-bit message block is

And the resulting 512-bit message digest is

531668966ee79b70 0b8e593261101354 4273f7ef7b31f279 2a7ef68d53f93264

319c165ad96d9187 55e6a204c2607e27 6e05cdf993a64c85 ef9e1e125c0f925f

The number of bit positions that differ between the two hash values is 253, almost exactly half the bit positions, indicating that SHA-512 has a good avalanche effect.