Chapter: Electric Energy Generation and Utilisation and Conservation : Solar Radiation and Solar Energy Collectors
Transmissivity of the Cover System on Flat Plate Collectors
Transmissivity of the Cover System
The transmissivity of the cover system of a collector can be obtained with adequate accuracy by considering reflection ŌĆō refraction and absorption separately and is given by the product form,

Transmissivity based on reflection ŌĆō refraction
When a beam of light of intensity Ibn travelling through a transparent medium 1 strikes the interface separating it from another transparent medium 2. It is reflected and refracted as shown in Fig.4.19. The reflected beam has a reduced indensity Ir and has a direction such that the angle of reflection is equal to the angle of incidence. On the other hand, the directions of the incident and reracted beams are related to each other by SnellŌĆÖs Law which states that,


Transmissivity based on Absorption
The Transmissivity based on absorption can be obtained by assuming that the attenuation due to absorption is proportional to the local intensity (BougerŌĆÖs law) . Consider a beam of intensity ŌĆśIbnŌĆÖ incident normally on a transparent cover of thickness ŌĆś╬┤cŌĆÖ and emerging with an intensity ŌĆśIlŌĆÖ as shown in Fig.4.21.
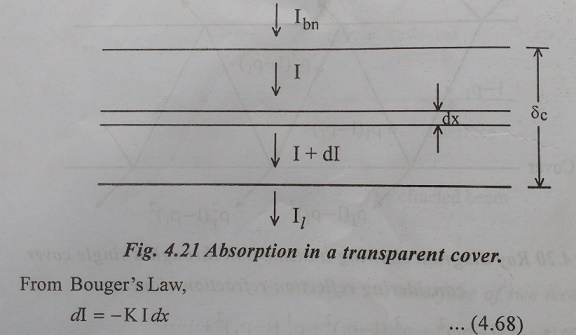
Where, K is a constant of proportionality and is called the extinction coefficient. It will be assumed to have a value independent of wavelength. Integrating over the length traversed by the beam, we have
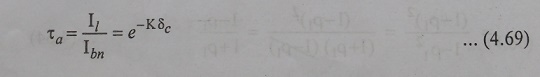
In case the beam is incident at an angle q1, the path traversed through the cover would be (╬┤c/cosq2), where q2 is the angle of refraction. Then Equ. (4.69) gets modified to the form,

The extinction coefficient K is a property of the cover material. Its value varies from about 4 to 25cm-1 for different qualities of glass. A low value is obviously desirable.
Equ.(4.69) and Equ.(4.70) are derived for one cover. If there are ŌĆśMŌĆÖ covers the exponent in these equations would be multiplied by ŌĆśMŌĆÖ.
Transmissivity for Diffuse Radiation
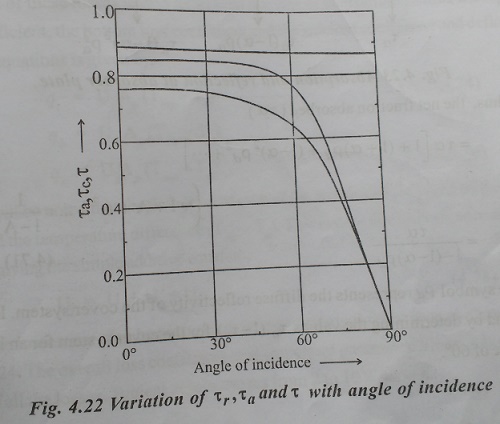
The preceding considerations apply only to beam radiation. Calculation of the transmissivity of a cover system when diffuse radiation is incident on it presents some difficulty; because the radiation comes from many directions. The usual practice is to assume that the diffuse radiation is equivalent to beam radiation coming at an angle of incidence of 60o. This angle is arrived at by considering the variation of ŌĆśtŌĆÖ as shown in ig.4.22, and by assuming that the amount of diffuse radiation coming from all directions is the same.
Related Topics