Chapter: Electric Energy Generation and Utilisation and Conservation : Solar Radiation and Solar Energy Collectors
Performance Analysis of Cylindrical Parabolic Concentrating Collector
Performance Analysis of Cylindrical Parabolic Concentrating Collector
Consider the performance analysis of a cylindrical parabolic concentrating collector whose concentrator has an aperature ŌĆśWŌĆÖ, length ŌĆśLŌĆÖ and rim angle ŌĆśŽĢrŌĆÖ, (Fig.4.30). The absorber tube has an inner diameter ŌĆśDiŌĆÖ and an outer diameter ŌĆśD0ŌĆÖ and it has concentric glass cover of inner diameter ŌĆśDciŌĆÖ and outer diameter ŌĆśDcoŌĆÖ around it. The fluid being heated in the collector has mass flow rate ŌĆśmŌĆÖ, a specific heat ŌĆśCpŌĆÖ, an inlet temperature ŌĆśTfiŌĆÖ and an outlet temperature ŌĆśTfoŌĆÖ.
The collector is operated in any one of the modes and the beam radiation normally incident on it aperture is Ibrb, whose value can be calculated from the equation derived. In some of the tracking modes, the SunŌĆÖs rays are incident at angle and will, there, come to a focus a little beyond the length of the concentractor. We assume that the absorber tube is long enough to intercept this image. In practice this would mean that the absorber tube might be a little longer (say about 10 per cent) than the concentrator and that the flux falling on the tube would not be uniform along the length. For the purposes of analysis, however, we will not take into account this extra tube length, and we will assume that the radiation flux is the same all along the length. We will also make the assumption that the temperature drop across the absorber tube and the glass cover are negligible.
The Concentration Ratio of the collector is given by,
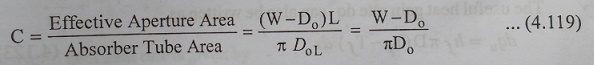
The analysis which follows is in many similar to the analysis of a liquid flat plate collectors. An energy balance on an elementary slice ŌĆśdxŌĆÖ of the absorber tube, at a distance ŌĆśxŌĆÖ from the inlet, yields the following equation for a steady state:


The first term on the right hand side Equ(4.120) represents the incident beam radiation absorbed in the absorber tube after reflection, while the second term represents the absorbed incident beam which falls directly on the absorber tube. The second term is small in comparison with the first, but cannot be ignored when the concentration ratio is small. The third term represents the loss by convection and radiation.
In manner similar to that adopted for a flat plate collector, we define an absorbed flux ŌĆśSŌĆÖ as follows,
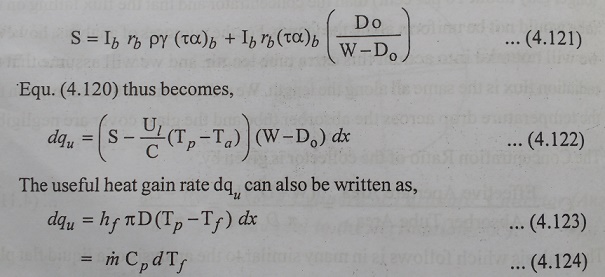


The fluid outlet temperature is obtained by putting Tf = Tfo and x=L in Equ(4.128). Making this substitution and subtracting both sides of the resulting equation from unity, we have
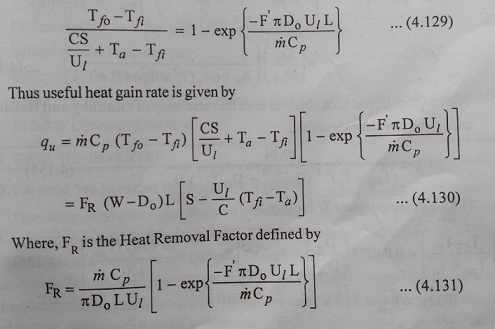
Equ.(4.130) is the equivalent of the ŌĆ£Hottel Whillier - BlissŌĆØ Equ(4.120) for a flat plate collector.
The Instantaneous Collection Efficiency (╬╝i) is given by
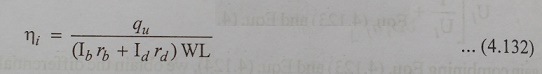
If the ground ŌĆō reflected radiation is neglected. The instantaneous efficiency can also be calculated on the basic of beam radiation alone, is given by,

Empirical Equation for the Overall Loss Coefficient
Based on calculation for a large number of cases covering a broad range of conditions encountered with cylindrical parabolic concentrating collectors, ŌĆ£Mullick and NandaŌĆØ have developed a semi empirical equation for directly calculating the overall Loss coefficient. This equation eliminates the need for an iterative calculation.
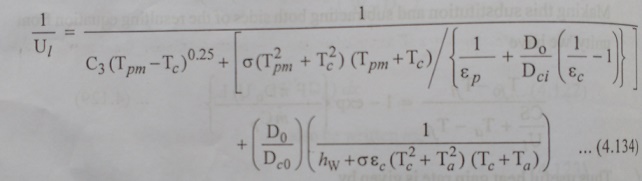
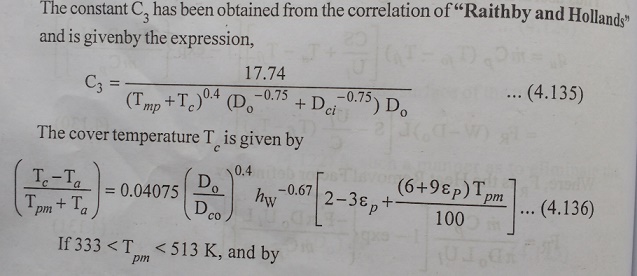
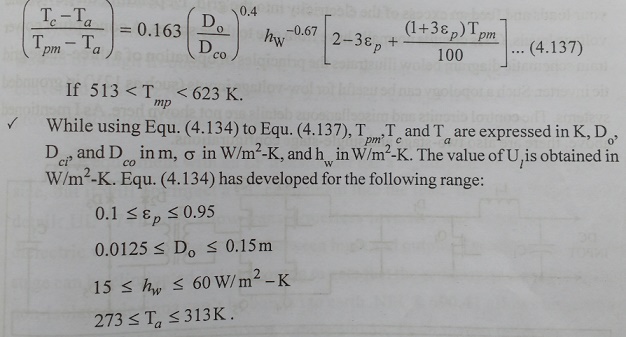

Related Topics