Chapter: Electric Energy Generation and Utilisation and Conservation : Solar Radiation and Solar Energy Collectors
Overall Loss Coefficient and Heat Transfer Correlations
Overall Loss Coefficient and Heat Transfer Correlations
It is convenient from the point of view of analysis to express the heat from the collector interms of an overall loss coefficient defined by the equation

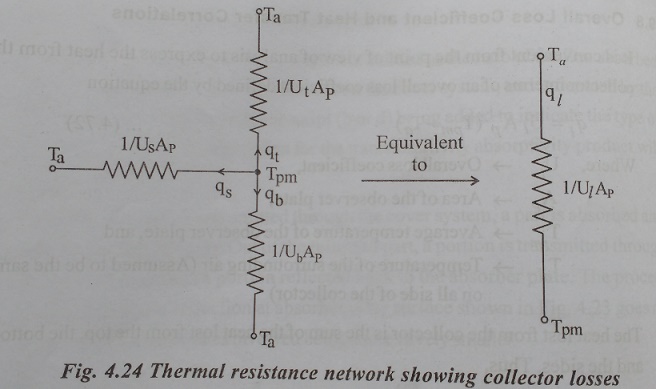
The heat lost from the collector is the sum of the heat lost from the top, the same and the sides. Thus

Each of these losses is also expressed interms of coefficients called the top loss coefficient, the bottom loss coefficient and the sideloss coefficient and defined by the equations is given by,
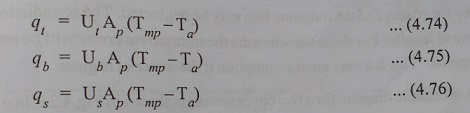
It will be noted that the definition of each of the coefficients is based on the area Ap and the temperature difference (Tmp-Ta). This is done for convenience and helps in giving the simple additive equation,

The losses can also be pictured in terms of thermal resistance as shown in Fig.4.24. The overall loss coefficient is an important parameter. Since, it is a measure of all the losses. Typical values ranges from 2 to 10W/m2-K.
Top Loss Coefficient
The top loss coefficient ŌĆśUtŌĆÖ is evaluated by considering convection and re-radiation losses from the absorber plate in the upward direction. For purposes of calculation, it is further assumed that the temperature drop across the thickness of the covers is negligible and that the interaction between the incoming solar radiation absorbed by the covers and the outgoing loss may be neglected. The re-radiation is of large wave lengths. For these wavelengths the transparent cover will be assumed to be opaque. This is a very good assumption if the material is glass.
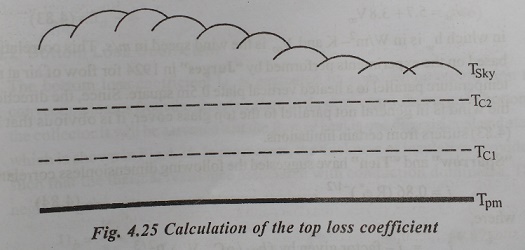
A schematic diagram for a two cover system is shown in ig.4.25. In a steady state the heat transferred by convection and radiation between (i) the absorption plate and the first cover, (ii) the first cover and second cover, and (iii) the second cover and the surrounding must be equal.
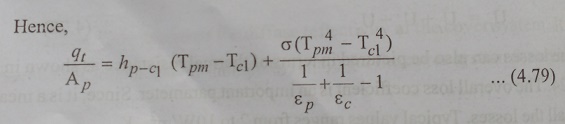


Bottom Loss Coefficient
The bottom loss Coefficient Ub is evaluated by considering conduction and convection losses from the absorber plate in the downward through the bottom of the collector. It will be assumed that the flow of heat is one dimensional and steady which is shown in ig.4.26. In most cases, the thickness of insulation provided is such that the thermal resistance associated with conduction dominates. Thus, neglecting the convective resistances, we have

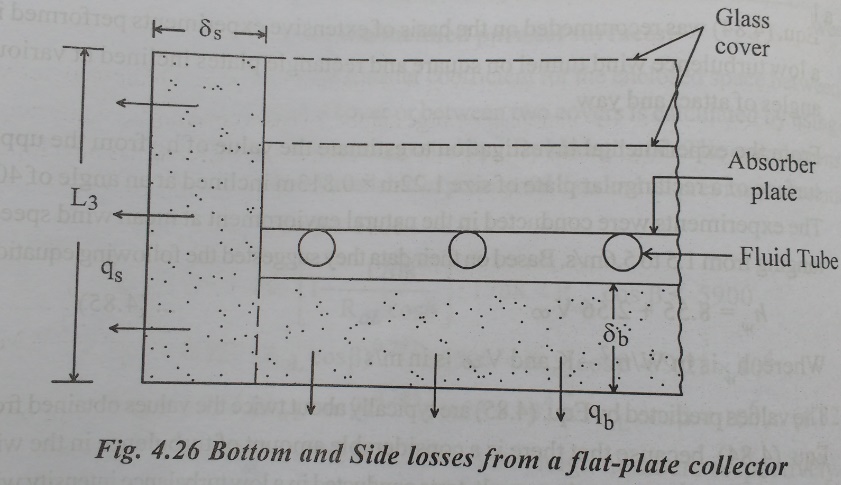
Side loss coefficient
While considering the bottom loss coefficient, it will be assumed that the conduction resistance dominates and that the low of heat is one-dimensional and steady. The one-dimensional approximation can be justified on the grounds that the side loss coefficient always much smaller than the top loss coefficient.
If the dimensions of the absorber plate are L1 x L2 and the height of the collector casing is L3, then the area across which heat flows sideways is 2(L1+L2)xL3. The temperature drop across which heat flows occurs varies from (Tpm-Ta) at the absorber plate level is zero both at the top and bottom. Assuming, therefore, that the average temperature drop across the side insulation is (Tpm-Ta)/2 and that the thickness of this insulation is ╬┤s, we have
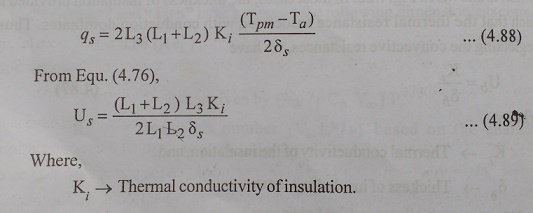
Empirical Equation for Top Loss Coefficient
Calculation of top loss coefficient by earlier method is require a tedious iterative calculation. Based on calculations for a large number of cases covering the entire range of conditions normally expected for flat plate collector, ŌĆ£KleinŌĆØ has developed the following convenient empirical equation for calculating the top loss coefficient.
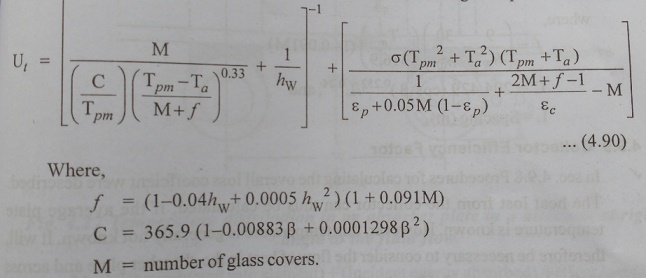
Related Topics