Three-Dimensional Viewing

THREE-DIMENSIONAL VIEWING

For three-dimensional applications, First of all, we can view an object from any spatial position: from the front, from above, or from the back. Or we could generate a view of what we would see if we were standing in the middle of a group of objects or inside a single object, such as a building. Additionally, three-dimensional descriptions of objects must be projected onto the flat viewing surface of the output device.

VIEWING COORDINATES

Generating a view of an object in three dimensions is similar to photographing the object. We can walk around and take its picture from any angle, at various distances, and with varying camera orientations. Whatever appears in the viewfinder is projected onto the flat film surface. The type and size of the camera lens determines which parts of the scene appear in the final picture.

These ideas are incorporated into three dimensional graphics packages so that views of a scene can be generated, given the spatial position, orientation, and aperture size of the "camera".

Specifying the View Plane

1.     We choose a particular view for a scene by first establishing the viewing-coordinate system, also called the view reference coordinate system. A view plane, or projection plane, is then set up perpendicular to the viewing z, axis.World-coordinate positions in the scene are transformed to viewing coordinates, then viewing coordinates are projected onto the view plane.To establish the viewing-coordinate reference frame, we first pick a world coordinate position called the view reference point.

PROJECTIONS

Once world-coordinate descriptions of the objects in a scene are converted to viewing coordinates, we can project the three-dimensional objects onto the triodimensional view plane.

There are two basic projection methods .

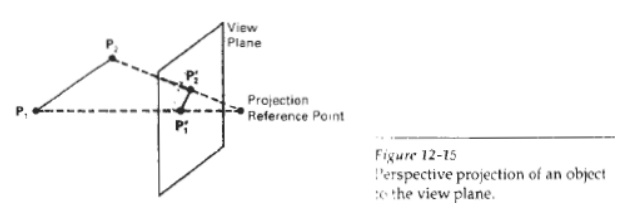
In a parallel projection, coordinate positions are transformed to the view plane along parallel lines For a perspective projection object positions are transformed to the view plane a!ong lines that converge to a point called the projection reference point (or center of projection).

The projected view of the object is determined by the interjection ofthe projection lines with the view z. plane.

Parallel Projections

We can specify a parallel projection with a projection vector that defines the directionfor the projection lines. When the projection is perpendicular to the view plane, we have an orthographic parallel projection. Otherwise, we have a oblique parallel projection.

Orthographic projections are most often used to produce the front, side, and top views of an object

Perspective projection

ⁿ   The center of projection is located at a finite point in three space.

ⁿ   A distant line is displayed smaller than a nearer line of the same length.

ⁿ   In three-dimensional homogeneous-coordinate representation

When a three-dimensional obpct is projected onto a view plane using per- hree-Dimensional Viewing spective transformation equations, any set of parallel lines in the object that are not parallel to the plane are projected into converging lines.

Parallel Lines that are parallel to the view plane will be projected as parallel lines.

vanishing point:

o        The point at which a set of projected parallel lines appears to converge is called a vanishing point.

o  Each such set of projected parallel lines will have a separate vanishing point;

o   And in general, a scene can have any number of vanishing points, depending on howmany sets of parallel lines there are in the scene.

o   The vanishing point for any set of lines that are parallel to one of the principal axes of an object is referred to as a principal vanishing point.

o   We control the number of principal vanishing points (one, two, or three) with the orientation of the projection plane, and perspective projections are accordingly classified as one-point, two-point, or three-point projections.

THREE-DIMENSIONAL VIEWING FUNCTIONS

Several procedures are usually provided in a three-dimensional graphics library to enable an application program to set the parameters for viewing transfonnations.

With parameters spenfied in world coordinates, elements of the matrix for transforming worldcoordinate descriptions to the viewing reference frame are calculated using the function evaluateViewOrientationMatrix3 (x0, y0,' Z0, xN, yN, zN, xv, yv, zV, error.,viewMatrix)

1. This function creates the viewMatrix from input coordinates defining the viewingsystem, 2. Parameters xo, yo, and z0 specify the origin (view reference point) of the viewing system. 3. World-coordinate vector defines the normal to the view plane and the direction of the positive, Three-Dimensional Viewing viewing axis. 4. And world-coordinate vector (xV, yv, zv) gives the elements of the view-up vector. The projection of this vector perpendicular to (xN, yN, zN) estab lishes the direction for the positive y, axis of the viewing system. 6. An integer error code is generated in parameter error if input values are not specified correctlyFor example, an error will be generated if we set (XV, YV, ZV) parallel to (xN, YN, zN)

To specify a second viewing-coordinate system, we can redefine some or allof the coordinate parameters and invoke evaluatevieworientationMatrix3 with a new matrix designation. In this way, we can set up any number of world-to-viewingcoordinate matrix transformations.