Three-Dimensional Geometric and Modeling Transformations

Three-Dimensional Geometric and Modeling Transformations

Methods for geometric transformations and object modeling in three dimensions are extended from two-dimensional methods by including considerations for the z coordinate.

We now translate an object by specifying a three-dimensional translation vector, which determines how much the object is tobe moved in each of the three coordinate directions. Similarly, we scale an object with three coordinate scaling factors.

TRANSLATION

In a three-dimensional homogeneous coordinate representation, a point is translated (Fig. 17-1) from position P = (x, y, z) to position P' = (x', y', z') with the matrix Operation

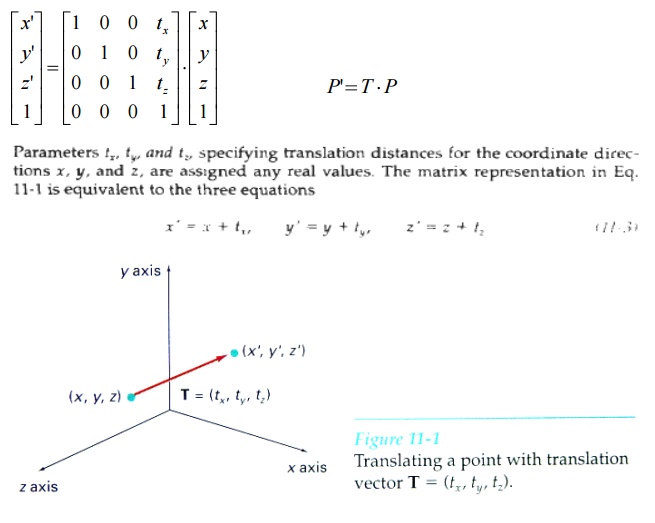
An object is translated in three dimensions by transforming each of the defining points of the object.

ROTATION

To generate a rotation transformation for an object, we must designate an axis of rotation (about which the object is to be rotated) and the amount of angular rotation.

Unlike two-dimensional applications, where all transformations are carried out in the xy plane, a three-dimensional rotation can be specified around any line in space.

The easiest rotation axes to handle are those that are parallel to the coordinate axes. Also, we can use combinations of coordinate axis rotations (along with appropriate translations) to specify any general rotation.

By convention, positive rotation angles produce counterclockwise rotations about a coordinate axis, if we are looking along the positive half of the axis toward the coordinate origin.

Coordinate-Axes Rotations

The two-dimensional z-axis rotation equations are easily extended to three dimensions:

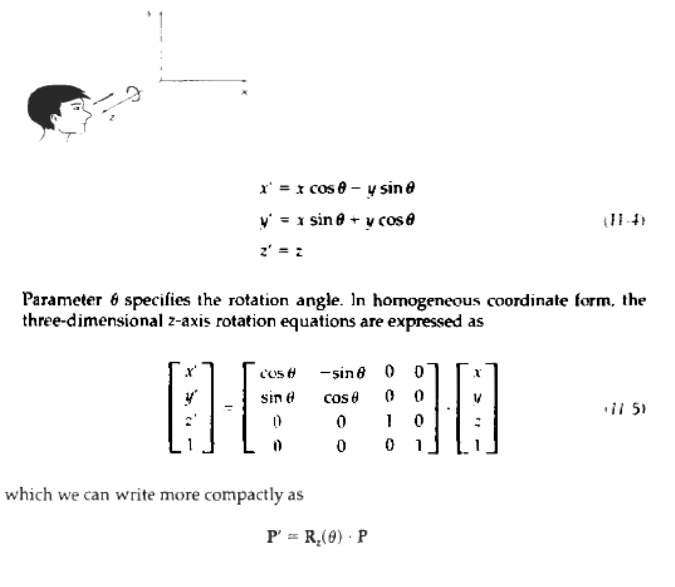
General Three-Dimensional Rotations

A rotation matrix for any axis that does not coincide with a coordinate axis can be set up as a composite transformation involving combinations of translations and the coordinate-axes rotations. .

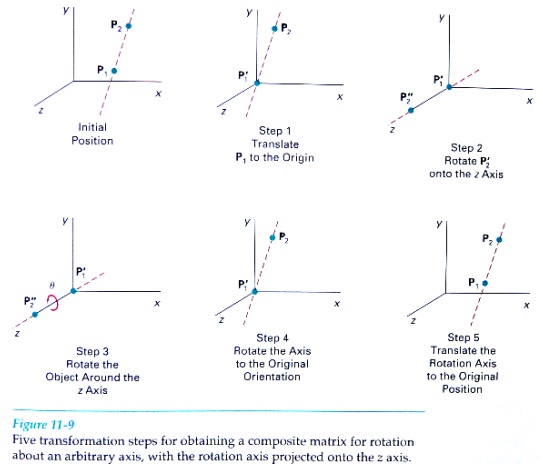
Any coordinate position P on the object in this figure is transformed with the sequence shown as

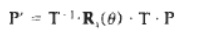
where the composite matrix for the transformation is

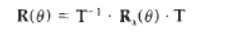
Given the specifications f or the rotation axis and the rotation angle, we can accomplish the required rotation in five s t e p

1 Translate the object so that the rotation axis pass= through the coordinate origin.

2. Rotate the object so that the axis of rotation coincides with one of the coordinate axes.

3. Perform the specified rotation about that coordinate axis.

4. Apply inverse rotations to bring the rotation axis back to original orientation.

5. Apply the inverse translation to bring the rotation axis back to its original position

A rotation axis can be defined with coordinate positions, as in fig or with one coordinate point and direction angles between the rotation axis and two of the coordinate axes. We will assume that the rotation axis is defined by two points and that the direction of rotation axes is to be counter clockwise when looking along the axis from P₁ to P₂

SCALING

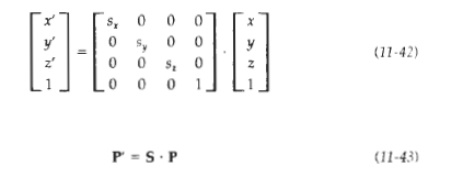
The matrix expression tor the scaling transformation of a position P = (x, y, z) relative to the coordinate origin can be written as

where scaling parameters sx, sy, and sz, are assigned any positive values. Explicit expressions for the coordinate transformations for scaling relative to the origin are

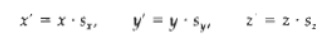
Scaling an object with transformation changes the size of the object and repositions the object relative to the coordinate origin. Also, if the transformation parameters are not all equal, relative dimensions in the object are changed:

Scaling with respect to a selected fixed position (x, y, z,) can be represented with the following transformation sequence:

1. Translate the fixed point to the origin.2. Scale the object relative to the coordinate origin using Eq. 11-42.3. Translate the fixed point back to its original position.

Reflections

A three-dimensional reflection can be performed relative to a selected reflection axis or with respect to a selected reception plane. In general, three-dimensional reflection matrices are set up similarly to those for two dimensions.

Reflections relative to a given axis are equivalent to 180 rotations about that axis. Reflections with respect to a plane are equivalent to 160' rotations in four-dimensional space.

When the reflection plane is a coordinate plane (either xy, xz, or yz), we can think of the transformation as a conversion between Left-handed and right-handed systems.

An example of a reflection that converts coordinate specifications from aright-handed system to a left-handed system (or vice versa)

This transformation changes the sign of the z coordinates, leaving the x and y-coordinate values unchanged. The matrix representation for this reflection of points relative to the xy plane is