Hidden Surface Elimination

HIDDEN SURFACE ELIMINATION

Hidden Surface Removal

When drawing lots of polygons, we want to draw only those ``visible'' to viewer. There are a variety of algorithms with different strong points.

Issues:

o   Online

o   Device independent

o   Fast

o   Memory requirements

o   Easy to implement in hardware

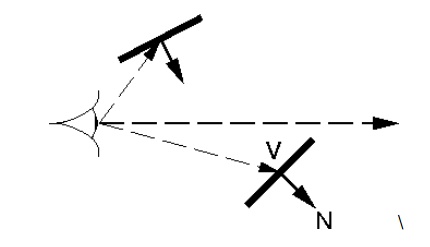
Backface CullingA simple way to perform hidden surface is to remove all ``backfacing'' polygons. The observation is that if polygon normal is facing away from the viewer then it is ``backfacing.'' For solid objects, this means the polygon will not be seen by the viewer.

·        Thus, if N.V > 0 , then cull polygon.

·        Note that V is vector from eye to point on polygon

You cannot use the view direction for this.

Backface Culling

Not a complete solution

·        If objects not convex, need to do more work.

·        If polygons two sided (i.e., they do not enclose a volume) then we can't use it.

·        A HUGE speed advantage if we can use it since the test is cheap and we expect at least half the polygons will be discarded.

·        Usually performed in conjunction with a more complete hidden surface algorithm.

·        Easy to integrate into hardware (and usually improves performance by a factor of 2).

Painter's Algorithm

Idea: Draw polygons as an oil painter might: The farthest one first. o Sort polygons on farthest z

o Resolve ambiguities where z's overlap 

o Scan convert from largest z to smallest z

Since closest drawn last, it will be on top (and therefore it will be seen).

Need all polygons at once in order to sort.

z-Buffer Algorithm

•The z or depth buffer–stores the depth of the closest object at each pixel

found so far As we render each polygon, compare the depth ofeach pixel to depth in z buffer

–If less, place the shade of pixel in the color buffer and update z buffer

Function setpixel(int i, int j, rgb c, real z) If z > z-buffer(i, j) then

z-buffer(i, j) = z screen(i,j) = c

Space Partitioning

•Avoid rendering an object when it’s unnecessary

–In many real-time applications, we want to eliminateas many objects as possible within the application.

Octree

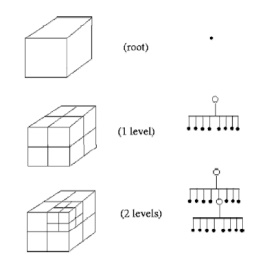
Why do we use BSP trees?

•Hidden surface removal

–A back-to-front painter’s algorithm

•Partition space with Binary Spatial Partition (BSP)Tree

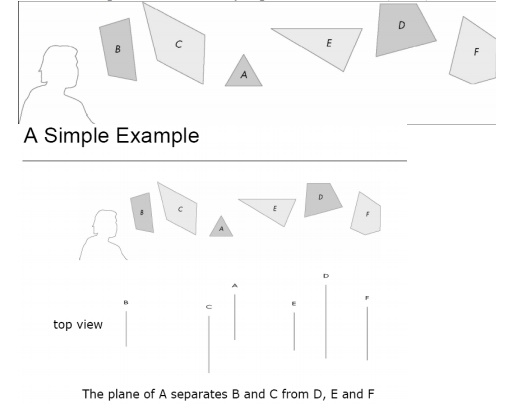
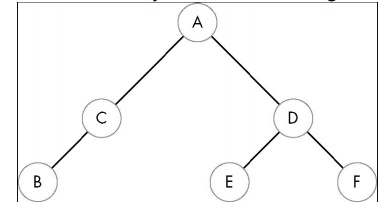
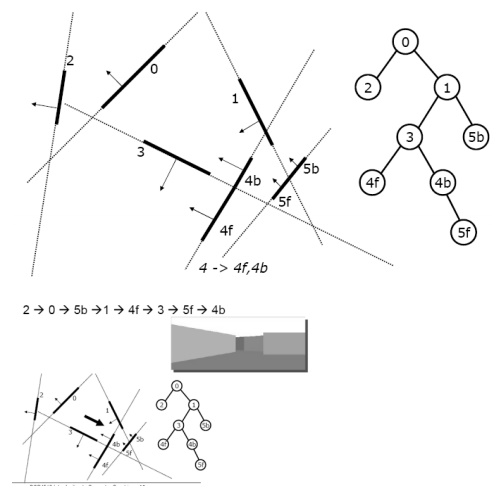
Binary Space Partitioning Tree

•Can continue recursively

–Plane of C separates B from A

–Plane of D separates E and F

•Can put this information in a BSP tree

–Use for visibility and occlusion testing

Key Idea of BSP

•Assume T2 not cross the plane of T1

•If e and T2 on the same side, T1 won’t block

•If e and T2 on different sides, T2 may block

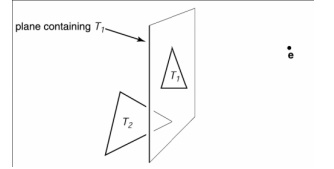
Creating a BSP tree