The physics of membrane potentials

The physics of membrane potentials

Both the resting and the action potential are diffusion potentials. A diffusion potential arises at a membrane if

1.  the membrane is selectively permeable for one or a few ion species,

2.  ls exist will therefore have a say in determining the membrane potential. Furthermore, as ion channels open and close, the changing permeabilities can shift the weight from one ion to the other. The most important example is the transient opening of sodium channels, which according to the Goldman equation will cause the membrane potential to shift toward the equilibrium potential.

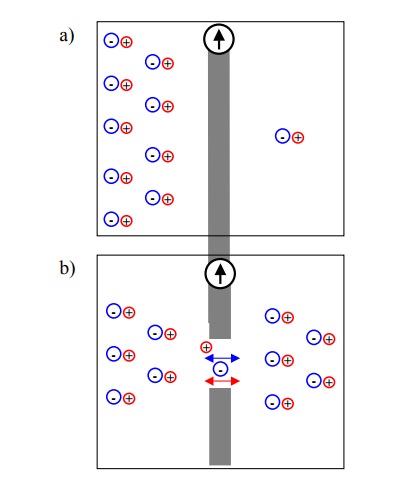
Figure 4.2a shows a membrane that has an ion gradient across it but is entirely impermeable; this will result in no membrane potential, as long as the numbers of anions and cations are the same within each adjoining compartment. 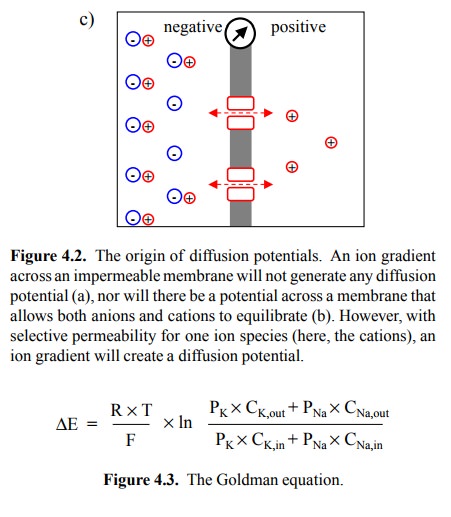In Figure 4.2b, the membrane has been rendered perme-able by a large, non-selective hole; both anions and cations are free to equilibrate across the membrane – again, there will be no membrane potential. In Figure 4.2c, the membrane contains channels that are selectively permeable to the cations. Diffusion of cations down their concentration gradient will create an imbalance of charge that in turn gives rise to a potential (a voltage gradient) across the membrane.

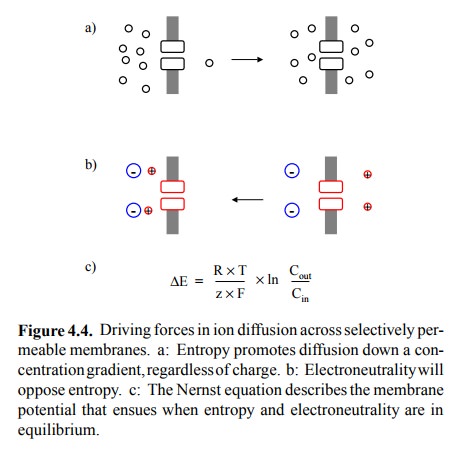
The migrating cations depicted in Figure 4.2c are subject to two driving forces that act in opposite directions: The concentration gradient will tend to drive any permeable species, regardless of its charge, across the membrane, until the concentrations are identical on both sides (Figure 4.4a); this is simply the maximization of entropy. Conversely, with progressing diffusion, the membrane potential will rise ever higher and tend to pull the cations back to the left side (Figure 4.4b). At some point, the two forces will be equally strong, and no further net ion movement will occur. This point is the equilibrium potential.

The equilibrium potential can be calculated from the Nernst equation, which is simply an application of the Gibbs equa-tion to ion gradients (Figure 4.4c)².

You will note that most terms in that equation are con-stants (the temperature is virtually constant at 37 °C = 310 K, too), so that the potential is essentially a function of the ion concentration gradient alone. However, this simple re-lationship will hold only when there is only one diffusible ion species. In a cell, we have several ion species, and fi-nite permeabilities for several of them. The two dominant cations, Na⁺ and K⁺, have roughly opposite distributions across the plasma membrane. Application of the Nernst equation to Na⁺ and K⁺ would yield membrane potentials of +60 mV and -90 mV, respectively³. Yet, the actual resting membrane potential is not identical to either of these values (which it would if the membrane were selectively perme-able to either K⁺ or Na⁺ only). Clearly, what we need is a means to determine the membrane potential if we have mul-tiple permeable ion species. This is provided by the Gold-man equation (given in Figure 4.3 in its special case for K⁺ and Na⁺). When comparing it with the Nernst equation, you see that the Goldman equation introduces one additional parameter P (for permeability), which has a specific value for each ion present.

Thus, the contribution of each ion to the overall membrane potential depends not only on its concentration but it is weighted for the permeability of the membrane for that ion. Since the concentrations and gradients for K⁺ and Na⁺ are of similar magnitude, we may infer that the membrane permeability must be larger for potassium than for sodium (P_K > P_Na), since the actual membrane potential is much closer to the K⁺ than to the Na⁺ equilibrium potential.

Now what's the molecular basis of different permeabili-ties for different ions? This is where the channels come in. Without a specific channel, no ion can effectively cross the membrane, so its permeability will be very small; only ions for which specific channels exist will therefore have a say in determining the membrane potential. Furthermore, as ion channels open and close, the changing permeabilities can shift the weight from one ion to the other. The most impor-tant example is the transient opening of sodium channels, which according to the Goldman equation will cause the membrane potential to shift toward the sodium equilibrium potential.