Syntax-Directed Translation

Syntax-Directed Translation

1 Postfix Notation

2 Synthesized Attributes

3 Simple Syntax-Directed Definitions

4 Tree Traversals

5 Translation Schemes

6 Exercises for Section 2.3

Syntax-directed translation is done by attaching rules or program fragments to productions in a grammar. For example, consider an expression expr generated by the production

                   expr   -»      exprx    +    term

Here, expr is the sum of the two subexpressions exprx    and term.  (The subscript in exprx    is       used only to distinguish the instance of expr in the production body from the head  of the  production).  We can  translate  expr by  exploiting its structure, as in the following pseudo-code:       

                   translate      exprx;        

                   translate      term;

                   handle +;             

Using a variant of this pseudocode, we shall build a syntax tree for expr in Section 2.8 by building syntax trees for expr_t and term and then handling + by constructing a node for it. For convenience, the example in this section is the translation of infix expressions into postfix notation.

This section introduces two concepts related to syntax-directed translation:

• Attributes. An attribute is any quantity associated with a programming construct. Examples of attributes are data types of expressions, the num-ber of instructions in the generated code, or the location of the first in-struction in the generated code for a construct, among many other pos-sibilities. Since we use grammar symbols (nonterminals and terminals) to represent programming constructs, we extend the notion of attributes from constructs to the symbols that represent them.

•        (Syntax-directed)  translation  schemes.  A  translation scheme  is  a notation    for attaching program fragments to the productions of a grammar.  The  program fragments are executed when the production is used during syn-        tax analysis.  The combined result of all these fragment executions,  in the order induced by the syntax analysis, produces the translation of the program to which this analysis/synthesis process is      applied.

Syntax-directed translations will be used throughout this chapter to trans-late infix expressions into postfix notation, to evaluate expressions, and to build syntax trees for programming constructs. A more detailed discussion of syntax-directed formalisms appears in Chapter 5.

1. Postfix Notation

The examples in this section deal with translation into postfix notation. The postfix notation for an expression E can be defined inductively as follows:

1. If E is a variable or constant, then the postfix notation for E is E itself.

2. If E is an expression of the form E1 op E₂, where op is any binary operator, then the postfix notation for E is E[ E'₂ op, where E[ and E'₂ are the postfix notations for E1 and E₂, respectively.

3.    If E is a parenthesized expression of the form (Ei), then the postfix notation for E is the same as the postfix notation for E1.

E x a m p l e 2.8 : The postfix notation for (9 - 5)+2 is 95-2+. That is, the trans-lations of 9, 5, and 2 are the constants themselves, by rule (1). Then, the translation of 9-5 is 95 - by rule (2). The translation of (9 - 5) is the same by rule (3). Having translated the parenthesized subexpression, we may apply rule (2) to the entire expression, with  (9 - 5) in the role of E1 and 2 in the role of E2: to get the result  95-2+.

As another example, the postfix notation for 9- (5+2) is 952+-. That is, 5+2 is first translated into 52+, and this expression becomes the second argument of the minus sign. •

No parentheses are needed in postfix notation, because the position and arity (number of arguments) of the operators permits only one decoding of a postfix expression. The "trick" is to repeatedly scan the postfix string from the left, until you find an operator. Then, look to the left for the proper number of operands, and group this operator with its operands. Evaluate the operator on the operands, and replace them by the result. Then repeat the process, continuing to the right and searching for another operator.

E x a m p l e 2 . 9 : Consider the postfix expression 952+-3*. Scanning from the left, we first encounter the plus sign. Looking to its left we find operands 5 and 2. Their sum, 7, replaces 52+, and we have the string 97 - 3* . Now, the leftmost operator is the minus sign, and its operands are 9 and 7. Replacing these by the result of the subtraction leaves 23*. Last, the multiplication sign applies to 2 and 3, giving the result 6. •

2. Synthesized Attributes

The idea of associating quantities with programming constructs—for example, values and types with expressions—can be expressed in terms of grammars. We associate attributes with nonterminals and terminals. Then, we attach rules to the productions of the grammar; these rules describe how the attributes are computed at those nodes of the parse tree where the production in question is used to relate a node to its children.

A      syntax-directed     definition      associates

            1. With each grammar symbol, a set of attributes, and

2. With each production, a set of semantic rules for computing the values of the attributes associated with the symbols appearing in the production.

Attributes can be evaluated as follows. For a given input string x, construct a parse tree for x. Then, apply the semantic rules to evaluate attributes at each node in the parse tree, as follows.

Suppose a node A?" in a parse tree is labeled by the grammar symbol X. We write X.a to denote the value of attribute a of X at that node. A parse tree showing the attribute values at each node is called an annotated parse tree. For example, Fig. 2.9 shows an annotated parse tree for 9-5+2 with an attribute t associated with the nonterminals expr and term. The value 95-2+ of the attribute at the root is the postfix notation for 9-5+2. We shall see shortly how  these expressions are computed.

An attribute is said to be synthesized if its value at a parse-tree node N is de-termined from attribute values at the children of N and at N itself. Synthesized attributes have the desirable property that they can be evaluated during a sin-gle bottom-up traversal of a parse tree. In Section 5.1.1 we shall discuss another important kind of attribute: the "inherited" attribute. Informally, inherited at-tributes have their value at a parse-tree node determined from attribute values at the node itself, its parent, and its siblings in the parse tree.

Example 2 . 1 0 : The annotated parse tree in Fig. 2 . 9 is based on the syntax-directed definition in Fig. 2 . 1 0 for translating expressions consisting of digits separated by plus or minus signs into postfix notation. Each nonterminal has a string-valued attribute t that represents the postfix notation for the expression generated by that nonterminal in a parse tree. The symbol || in the semantic rule is the operator for string concatenation.

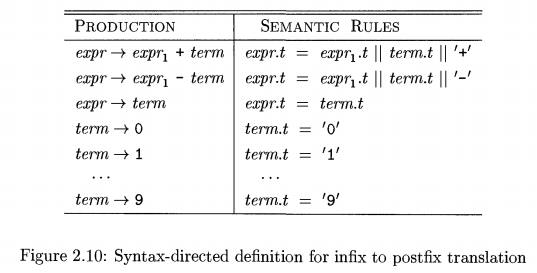
The postfix form of a digit is the digit itself; e.g., the semantic rule associ-ated with the production term -» 9 defines term.t to be 9 itself whenever this production is used at a node in a parse tree. The other digits are translated similarly.   As another example, when the production expr term is applied,  the value of term.t becomes the value of expr.t.

The production expr —> expr_x + term derives an expression containing a plus operator.³ The left operand of the plus operator is given by expr_x and the right operand by term. The semantic rule

expr.t                           =  expr.t  \\  term.t  \\  '+'

associated with this production constructs the value of attribute expr.t by con-catenating the postfix forms expr.t and term.t of the left and right operands, respectively, and then appending the plus sign. This rule is a formalization of the definition of "postfix expression." •

Convention Distinguishing Uses of a Nonterminal

In rules, we often have a need to distinguish among several uses of the same nonterminal in the head and/or body of a production; e.g., see Ex-ample 2.10. The reason is that in the parse tree, different nodes labeled by the same nonterminal usually have different values for their transla-tions. We shall adopt the following convention: the nonterminal appears unsubscripted in the head and with distinct subscripts in the body. These are all occurrences of the same nonterminal, and the subscript is not part of its name. However, the reader should be alert to the difference be-tween examples of specific translations, where this convention is used, and generic productions like A —> X1X2, • • • ,X_n, where the subscripted X ' s represent an arbitrary list of grammar symbols, and are not instances of one particular nonterminal called X.

3. Simple Syntax-Directed Definitions

The syntax-directed definition in Example 2.10 has the following important property: the string representing the translation of the nonterminal at the head of each production is the concatenation of the translations of the nonterminals in the production body, in the same order as in the production, with some optional additional strings interleaved. A syntax-directed definition with this property is termed simple.

E x a m p l e 2 . 1 1 :  Consider the first production and semantic rule from Fig. 2.10:

P R O D U C T I O N                     S E M A N T I C         R U L E

(2.5)

expr^r        expr_x   +          term  expr.t =       exprx.t  ||  term.t  ||  '+'

Here the translation expr.t is the concatenation of the translations of expr_x and term, followed by the symbol +. Notice that expr1 and term appear in the same order in both the production body and the semantic rule. There are no additional symbols before or between their translations. In this example, the only extra symbol occurs at the end. •

When translation schemes are discussed, we shall see that a simple syntax-directed definition can be implemented by printing only the additional strings, in the order they appear in the definition.

4. Tree Traversals

Tree traversals will be used for describing attribute evaluation and for specifying the execution of code fragments in a translation scheme. A traversal of a tree starts at the root and visits each node of the tree in some order.

A depth-first traversal starts   at the root  and recursively visits the          children of each node in any order, not necessarily from left to right.  It is called "depth-first" because it visits an unvisited child of a node whenever it can, so it visits nodes as far away from the root (as "deep") as quickly as it can.

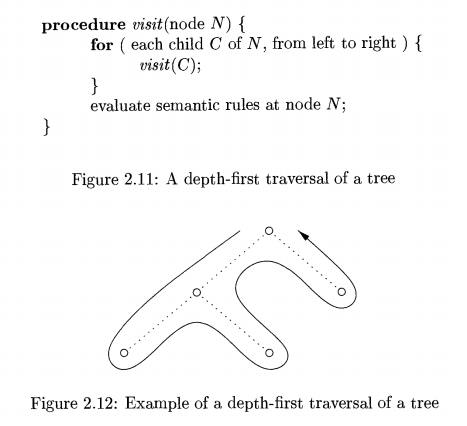
The procedure visit(N) in Fig. 2.11 is a depth first traversal that visits the children of a node in left-to-right order, as shown in Fig. 2.12. In this traversal, we have included the action of evaluating translations at each node, just before we finish with the node (that is, after translations at the children have surely been computed). In general, the actions associated with a traversal can be

whatever we choose, or nothing at all.

A syntax-directed definition does not impose any specific order for the eval-uation of attributes on a parse tree; any evaluation order that computes an attribute a after all the other attributes that a depends on is acceptable. Syn-thesized attributes can be evaluated during any bottom-up traversal, that is, a traversal that evaluates attributes at a node after having evaluated attributes at its children. In general, with both synthesized and inherited attributes, the matter of evaluation order is quite complex; see Section 5.2.

5. Translation Schemes

The syntax-directed definition in Fig. 2.10 builds up a translation by attaching strings as attributes to the nodes in the parse tree. We now consider an alter-native approach that does not need to manipulate strings; it produces the same translation incrementally, by executing program fragments.

Preorder and Postorder Traversals

Preorder and postorder traversals are two important special cases of depth-first traversals in which we visit the children of each node from left to right.

Often,  we traverse a tree to perform some particular action at each node.          If the action is done when we first visit a node, then we may refer to the traversal as  a preorder traversal. Similarly,  if the  action  is  done just before we leave a node for the last time, then we say it is a postorder traversal of the tree. The procedure visit(N) in Fig. 2.11 is an example of a postorder traversal.

Preorder and postorder traversals define corresponding orderings on nodes, based on when the action at a node would be performed. The preorder of a (sub)tree rooted at node JV consists of N, followed by the preorders of the subtrees of each of its children, if any, from the left. The postorder of a (sub)tree rooted at TV" consists of the postorders of each of the subtrees for the children of N, if any, from the left, followed by N itself.

A syntax-directed translation scheme is a notation for specifying a transla-tion by attaching program fragments to productions in a grammar. A transla-tion scheme is like a syntax-directed definition, except that the order of evalu-ation of the semantic rules is explicitly specified.

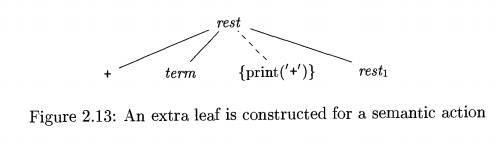
Program fragments embedded within production bodies are called semantic actions. The position at which an action is to be executed is shown by enclosing it between curly braces and writing it within the production body, as in

rest                         —> + term              {print('+')}       rest\

We shall see such rules when we consider an alternative form of grammar for expressions, where the nonterminal rest represents "everything but the first term of an expression." This form of grammar is discussed in Section 2.4.5. Again, the subscript in rest\ distinguishes this instance of nonterminal rest in the production body from the instance of rest at the head of the production.

When drawing a parse tree for a translation scheme, we indicate an action by constructing an extra child for it, connected by a dashed line to the node that corresponds to the head of the production. For example, the portion of the parse tree for the above production and action is shown in Fig. 2.13. The node for a semantic action has no children, so the action is performed when that node is first seen.

E x a m p l e 2 . 1 2 : The parse tree in Fig. 2.14 has print statements at extra leaves, which are attached by dashed lines to interior nodes of the parse tree. The translation scheme appears in Fig. 2.15. The underlying grammar gen-erates expressions consisting of digits separated by plus and minus signs. The

actions embedded in the production bodies translate such expressions into post-fix notation, provided we perform a left-to-right depth-first traversal of the tree and execute each print statement when we visit its leaf.

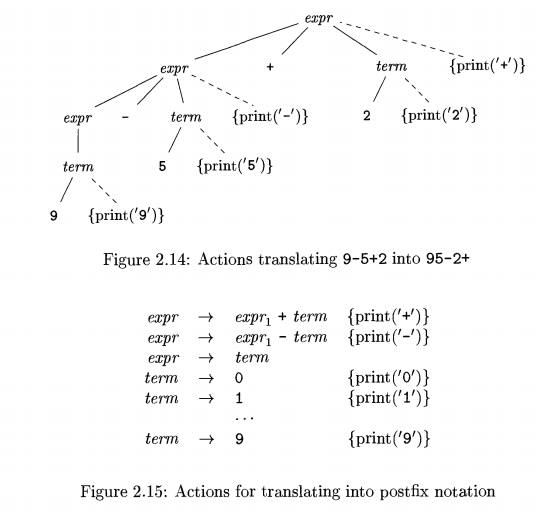
The root of Fig. 2.14 represents the first production in Fig. 2.15. In a postorder traversal, we first perform all the actions in the leftmost subtree of the root, for the left operand, also labeled expr like the root. We then visit the leaf + at which there is no action. We next perform the actions in the subtree for the right operand term and, finally, the semantic action { print('+') } at the extra node.

Since the productions for term have only a digit on the right side, that digit is printed by the actions for the productions. No output is necessary for the production expr -> term, and only the operator needs to be printed in the action for each of the first two productions. When executed during a postorder traversal of the parse tree, the actions in Fig. 2.14 print 95-2+. •

Note that although the schemes in Fig. 2.10 and Fig. 2.15 produce the same translation, they construct it differently; Fig. 2.10 attaches strings as attributes to the nodes in the parse tree, while the scheme in Fig. 2.15 prints the translation incrementally, through semantic actions.

The semantic actions in the parse tree in Fig. 2.14 translate the infix ex-pression 9-5+2 into 95-2+ by printing each character in 9-5+2 exactly once, without using any storage for the translation of subexpressions. When the out-put is created incrementally in this fashion, the order in which the characters are printed is significant.

The implementation of a translation scheme must ensure that semantic ac-tions are performed in the order they would appear during a postorder traversal of a parse tree. The implementation need not actually construct a parse tree (often it does not), as long as it ensures that the semantic actions are per-formed as if we constructed a parse tree and then executed the actions during a postorder traversal.

6. Exercises for Section 2.3

Exercise 2 . 3 . 1 : Construct a syntax-directed translation scheme that trans-lates arithmetic expressions from infix notation into prefix notation in which an operator appears before its operands; e.g., —xy is the prefix notation for x — y. Give annotated parse trees for the inputs 9-5+2 and 9-5*2.

Exercise 2 . 3 . 2: Construct a syntax-directed translation scheme that trans-lates arithmetic expressions from postfix notation into infix notation. Give annotated parse trees for the inputs 95 - 2* and 952* - .

Exercise 2 . 3 . 3: Construct a syntax-directed translation scheme that trans-lates integers into roman numerals.

Exercise 2 . 3 . 4: Construct a syntax-directed translation scheme that trans-lates roman numerals into integers.

Exercise 2 . 3 . 5: Construct a syntax-directed translation scheme that trans-lates postfix arithmetic expressions into equivalent infix arithmetic expressions.