Intermediate Code Generation

Intermediate Code Generation

1 Two Kinds of Intermediate Representations

2 Construction of Syntax Trees

3 Static Checking

4 Three-Address Code

5 Exercises for Section 2.8

The front end of a compiler constructs an intermediate representation of the source program from which the back end generates the target program. In this section, we consider intermediate representations for expressions and state-ments, and give tutorial examples of how to produce such representations.

1. Two Kinds of Intermediate Representations

As was suggested in Section 2.1 and especially Fig. 2.4, the two most important intermediate representations are:

^{1 0} I n s t e ad of explicitly saving and restoring tables, we could alternatively add static opera-tions push and pop to class Env.

•  Trees, including parse trees and (abstract) syntax trees.

•  Linear representations, especially  "three-address code."

Abstract-syntax trees, or simply syntax trees, were introduced in Section 2.5.1, and in Section 5.3.1 they will be reexamined more formally. During parsing, syntax-tree nodes are created to represent significant programming constructs. As analysis proceeds, information is added to the nodes in the form of attributes associated with the nodes. The choice of attributes depends on the translation to be performed.

Three-address code, on the other hand, is a sequence of elementary program steps, such as the addition of two values. Unlike the tree, there is no hierarchical structure.  As we shall see in Chapter 9, we need this representation if we are to do any significant optimization of code. In that case,  we break the long sequence of three-address statements that form a program into "basic blocks," which are sequences of statements that are always executed one-after-the-other, with no branching.

In addition to creating an intermediate representation, a compiler front end checks that the source program follows the syntactic and semantic rules of the source language. This checking is called static checking; in general "static" means "done by the compiler."^{1 1} Static checking assures that certain kinds of programming errors, including type mismatches, are detected and reported during compilation.

It is possible that a compiler will construct a syntax tree at the same time it emits steps of three-address code. However, it is common for compilers to emit the three-address code while the parser "goes through the motions" of constructing a syntax tree, without actually constructing the complete tree data structure. Rather, the compiler stores nodes and their attributes needed for semantic checking or other purposes, along with the data structure used for parsing. By so doing, those parts of the syntax tree that are needed to construct the three-address code are available when needed, but disappear when no longer needed. We take up the details of this process in Chapter 5.

2. Construction of Syntax Trees

We shall first give a translation scheme that constructs syntax trees, and later, in Section 2.8.4, show how the scheme can be modified to emit three-address code, along with, or instead of, the syntax tree.

Recall from Section 2.5.1 that the syntax tree

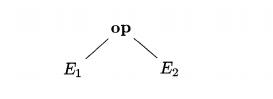
represents an expression formed by applying the operator op to the subexpres-sions represented by E1 and E₂. Syntax trees can be created for any construct, not just expressions. Each construct is represented by a node, with children for the semantically meaningful components of the construct. For example, the semantically meaningful components of a C while-statement:

while  (  expr )                              stmt

are the expression expr and the statement stmt.¹² The syntax-tree node for such a while-statement has an operator, which we call while, and two children—the syntax trees for the expr and the stmt.

The translation scheme in Fig. 2.39 constructs syntax trees for a repre-sentative, but very limited, language of expressions and statements. All the nonterminals in the translation scheme have an attribute n, which is a node of the syntax tree. Nodes are implemented as objects of class Node.

Class Node has two immediate subclasses: Expr for all kinds of expressions, and Stmt for all kinds of statements. Each type of statement has a corresponding subclass of Stmt; for example, operator while corresponds to subclass While. A syntax-tree node for operator while with children x and y is created by the pseudocode

new   While (x,y)

which creates an object of class  While by calling constructor function  While, with the same name as the class. Just as constructors correspond to operators, constructor parameters correspond to operands in the abstract syntax.

When we study the detailed code in Appendix A, we shall see how methods are placed where they belong in this hierarchy of classes. In this section, we shall discuss only a few of the methods, informally.

We shall consider each of the productions and rules of Fig. 2.39, in turn . First, the productions defining different types of statements are explained, fol-lowed by the productions that define our limited types of expressions.

Syntax  Trees for Statements

For each statement construct, we define an operator in the abstract syntax. For constructs that begin with a keyword, we shall use the keyword for the operator. Thus, there is an operator while for while-statements and an operator do for do-while statements. Conditionals can be handled by defining two operators

ifelse and if for if-statements with and without an else part, respectively. In our simple example language, we do not use else, and so have only an if-statement. Adding else presents some parsing issues, which we discuss in Section 4.8.2.

Each statement operator has a corresponding class of the same name, with a capital first letter; e.g., class If corresponds to if. In addition, we define the subclass Seq, which represents a sequence of statements. This subclass corresponds to the nonterminal stmts of the grammar. Each of these classes are subclasses of Stmt, which in turn is a subclass of Node.

The translation scheme in Fig. 2.39 illustrates the construction of syntax-tree nodes. A typical rule is the one for if-statements:

stmt ->• if ( expr ) stmti { stmt.n = new If (expr.n, stmt\.n); }

The meaningful components of the if-statement are expr and stmt\. The semantic action defines the node stmt.n as a new object of subclass If. The code for the constructor // is not shown. It creates a new node labeled if with the nodes expr.n and stmt\.n as children.

Expression statements do not begin with a keyword, so we define a new op-erator eval and class Eval, which is a subclass of Stmt, to represent expressions that are statements. The relevant rule is:

stmt -> expr ; { stmt.n = new Eval (expr.n); }

Representing Blocks in Syntax Trees

The remaining statement construct in Fig. 2.39 is the block, consisting of a sequence of statements. Consider the rules:

stmt -» block { stmt.n = block.n; }

block -» '{' stmts '}' { block.n = stmts.n; }

The first says that when a statement is a block, it has the same syntax tree as the block. The second rule says that the syntax tree for nonterminal block is simply the syntax tree for the sequence of statements in the block.

For simplicity, the language in Fig. 2.39 does not include declarations. Even when declarations are included in Appendix A, we shall see that the syntax tree for a block is still the syntax tree for the statements in the block. Since information from declarations is incorporated into the symbol table, they are not needed in the syntax tree. Blocks, with or without declarations, therefore appear to be just another statement construct in intermediate code.

A sequence of statements is represented by using a leaf null for an empty statement and a operator seq for a sequence of statements, as in

stmts -*• stmtsi stmt { stmts.n = n e w Seq(stmts1.n, stmt.n); }

Example     2 . 1 8 :  In Fig. 2.40 we see part of a syntax tree representing a block or statement list. There are two statements in the list, the first an if-statement and the second a while-statement. We do not show the portion of the tree above this statement list, and we show only as a triangle each of the necessary subtrees: two expression trees for the conditions of the if- and while-statements, and two statement trees for their substatements. •

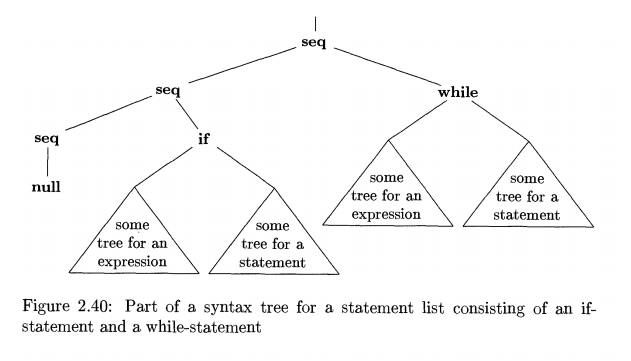
Figure 2.40: Part of a syntax tree for a statement list consisting of an if-statement and a while-statement

Syntax  Trees for Expressions

Previously, we handled the higher precedence of * over + by using three non-terminals expr, term, and factor. The number of nonterminals is precisely one plus the number of levels of precedence in expressions, as we suggested in Sec-tion 2.2.6. In Fig. 2.39, we have two comparison operators, < and <= at one precedence level, as well as the usual + and * operators, so we have added one additional nonterminal, called add.

Abstract syntax allows us to group "similar" operators to reduce the number of cases and subclasses of nodes in an implementation of expressions. In this chapter, we take "similar" to mean that the type-checking and code-generation rules for the operators are similar. For example, typically the operators + and * can be grouped, since they can be handled in the same way — their requirements regarding the types of operands are the same, and they each result in a single three-address instruction that applies one operator to two values. In general, the grouping of operators in the abstract syntax is based on the needs of the later phases of the compiler. The table in Fig. 2.41 specifies the correspondence between the concrete and abstract syntax for several of the operators of Java.

In the concrete syntax, all operators are left associative, except the assign-ment operator =, which is right associative. The operators on a line have the

same precedence; that is, == and != have the same precedence. The lines are in order of increasing precedence; e.g., == has higher precedence than the oper-ators && and =. The subscript unary in - unary is solely to distinguish a leading unary minus sign, as in - 2 , from a binary minus sign, as in 2-a. The operator [] represents array access, as in a [ i ] .

The abstract-syntax column specifies the grouping of operators. The assign-ment operator = is in a group by itself. The group cond contains the conditional boolean operators && and I I. The group rel contains the relational comparison operators on the lines for == and <. The group op contains the arithmetic operators like + and *. Unary minus, boolean negation, and array access are in groups by themselves.

The mapping between concrete and abstract syntax in Fig. 2.41 can be implemented by writing a translation scheme. The productions for nonterminals expr, rel, add, term, and factor in Fig. 2.39 specify the concrete syntax for a representative subset of the operators in Fig. 2.41. The semantic actions in these productions create syntax-tree nodes. For example, the rule

term —b termi  * factor {  term.n = n e w  Op(V,term\ . n,factor . n);  }

creates a node of class Op, which implements the operators grouped under op in Fig.  2.41. The constructor  Op has a parameter '*' to identify the actual operator, in addition to the nodes  termy.n and factor.n for the subexpressions.

3. Static Checking

Static checks are consistency checks that are done during compilation. Not only do they assure that a program can be compiled successfully, but they also have the potential for catching programming errors early, before a program is run. Static checking includes:

• Syntactic Checking. There is more to syntax than grammars. For ex-ample, constraints such as an identifier being declared at most once in a scope, or that a break statement must have an enclosing loop or switch statement, are syntactic, although they are not encoded in, or enforced by, a grammar used for parsing.

• Type Checking. The type rules of a language assure that an operator or function is applied to the right number and type of operands. If conversion between types is necessary, e.g., when an integer is added to a float, then the type-checker can insert an operator into the syntax tree to represent that conversion. We discuss type conversion, using the common term "coercion," below.

L - values  and  R - values

We now consider some simple static checks that can be done during the con-struction of a syntax tree for a source program. In general, complex static checks may need to be done by first constructing an intermediate representation and then analyzing it.

There is a distinction between the meaning of identifiers on the left and right sides of an assignment. In each of the assignments

i = 5 ;

i = i + 1;

the right side specifies an integer value, while the left side specifies where the value is to be stored. The terms l-value and r-value refer to values that are appropriate on the left and right sides of an assignment, respectively. That is, r-values are what we usually think of as "values," while /-values are locations.

Static checking must assure that the left side of an assignment denotes an /-value. An identifier like i has an /-value, as does an array access like a [ 2 ] .

But a constant like 2 is not appropriate on the left side of an assignment, since it has an r-value, but not an /-value.

Type Checking

Type checking assures that the type of a construct matches that expected by its context. For example, in the if-statement

if ( expr ) stmt

the expression expr is expected to have type boolean .

Type checking rules follow the operator/operand structure of the abstract syntax. Assume the operator rel represents relational operators such as <=. The type rule for the operator group rel is that its two operands must have the same type, and the result has type boolean. Using attribute type for the type of an expression, let E consist of rel applied to Ei and E2. The type of E can be checked when its node is constructed, by executing code like the following:

if ( Ei.type == E2.type ) E.type = boolean;

 else error;

The idea of matching actual with expected types continues to apply, even in the following situations:

• Coercions. A coercion occurs if the type of an operand is automatically  converted to the type expected by the operator. In an expression like 2 * 3 . 14, the usual transformation is to convert the integer 2 into an equivalent floating-point number, 2 . 0 , and then perform a floating-point operation on the resulting pair of floating-point operands. The language definition specifies the allowable coercions. For example, the actual rule for rel discussed above might be that Ei.type and E2.type are convertible to the same type. In that case, it would be legal to compare, say, an integer with a float.

• Overloading. The operator + in Java represents addition when applied to integers; it means concatenation when applied to strings. A symbol is said to be overloaded if it has different meanings depending on its context.  Thus, + is overloaded in Java. The meaning of an overloaded operator is determined by considering the known types of its operands and results. For example, we know that the + in z = x + y is concatenation if we know that any of x, y, or z is of type string. However, if we also know that another one of these is of type integer, then we have a type error and there is no meaning to this use of +. 

4. Three-Address Code

Once syntax trees are constructed, further analysis and synthesis can be done by evaluating attributes and executing code fragments at nodes in the tree. We illustrate the possibilities by walking syntax trees to generate three-address code. Specifically, we show how to write functions that process the syntax tree and, as a side-effect, emit the necessary three-address code.

Three - Address   Instructions

Three-address code is a sequence of instructions of the form

x - y op z

where x, y, and z are names, constants, or compiler-generated temporaries; and op stands for an operator.

Arrays will be handled by using the following two variants of instructions:

x [ y ] - z x = y [ z 1

The first puts the value of z in the location x[y], and the second puts the value of y[z] in the location x.

Three-address instructions are executed in numerical sequence unless forced to do otherwise by a conditional or unconditional jump . We choose the following instructions for control flow:

if False x goto L if £ is false, next execute the instruction labeled L if True x goto L if rc is true, next execute the instruction labeled L goto L next execute the instruction labeled L

A label L can be attached to any instruction by prepending a prefix L:. An instruction can have more than one label.

Finally, we need instructions that copy a value. The following three-address instruction copies the value of y into x:

x= y

Translation of Statements

Statements are translated into three-address code by using jump instructions to implement the flow of control through the statement. The layout in Fig. 2.42 illustrates the translation of if expr t h e n stmti. The jump instruction in the layout

if False x goto after

jumps over the translation of stmti if expr evaluates to false. Other statement constructs are similarly translated using appropriate jumps around the code for their components.

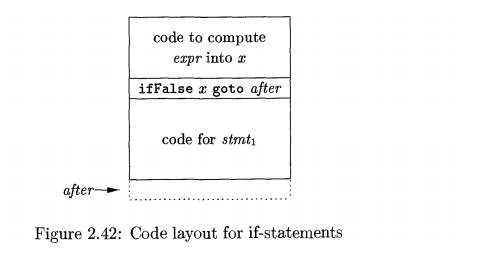
For concreteness, we show the pseudocode for class If in Fig. 2.43. Class

If is a subclass of Stmt, as are the classes for the other statement constructs.

Each subclass of Stmt has a constructor — // in this case — and a function gen that is called to generate three-address code for this kind of statement.

class // extends Stmt {

 Expr E; Stmt S;

 public If (Expr x, Stmt y) { E = x; S = y; after = newlabelQ; }

 public void gen() {

 Expr n = E.rvalueQ;

 emit( "ifFalse " + n.toStringQ + " goto " + after);

 S.genQ; 

 emit (after + ":");

}

Figure 2.43: Function gen in class //generates three-address code

 The constructor // in Fig. 2.43 creates syntax-tree nodes for if-statements. It is called with two parameters, an expression node x and a statement node y, which it saves as attributes E and 5. The constructor also assigns attribute after a unique new label, by calling function newlabelQ. The label will be used according to the layout in Fig. 2.42.

Once the entire syntax tree for a source program is constructed, the function gen is called at the root of the syntax tree. Since a program is a block in our simple language, the root of the syntax tree represents the sequence of statements in the block. All statement classes contain a function gen.

The pseudocode for function gen of class / / i n Fig. 2.43 is representative. It calls E.rvalueQ to translate the expression E (the boolean-valued expression that is part of the if-statements) and saves the result node returned by E.

Translation of expressions will be discussed shortly. Function gen then emits a conditional jump and calls S.genQ to translate the substatement S.

Translation  of Expressions

We now illustrate the translation of expressions by considering expressions con-taining binary operators op, array accesses, and assignments, in addition to constants and identifiers. For simplicity, in an array access y[z], we require that y be an identifier.^{1 3}       For a detailed discussion of intermediate code generation for expressions, see Section 6.4.

We shall take the simple approach of generating one three-address instruc-tion for each operator node in the syntax tree for an expression. No code is generated for identifiers and constants, since they can appear as addresses in instructions. If a node x of class Expr has operator op, then an instruction is emitted to compute the value at node x into a compiler generated "temporary" name, say t. Thus, i - j + k translates into two instructions

^{1 3} This simple language supports a[a[n]], but not a[m] [n]. Note that a[a[n]] has the form a [£?], where E is a [n].

tl = i - j

 t2 = tl + k

With array accesses and assignments comes the need to distinguish between /-values and r-values. For example, 2 * a [ i ] can be translated by computing the r-value of a [ i ] into a temporary, as in

tl = a [ i ]

t2 = 2 * tl

But, we cannot simply use a temporary in place of a [ i ] , if a [ i ] appears on the left side of an assignment.

The simple approach uses the two functions lvalue and rvalue, which appear in Fig. 2.44 and 2.45, respectively. When function rvalue is applied to a nonleaf node x, it generates instructions to compute x into a temporary, and returns a new node representing the temporary. When function lvalue is applied to a nonleaf, it also generates instructions to compute the subtrees below x, and returns a node representing the "address" for x.

We describe function lvalue first, since it has fewer cases. When applied to a node x, function lvalue simply returns x if it is the node for an identifier (i.e., if x is of class Id). In our simple language, the only other case where an expression has an /-value occurs when x represents an array access, such as a [ i ] . In this case, x will have the form Access(y, z), where class Access is a subclass of Expr, y represents the name of the accessed array, and z represents the offset (index) of the chosen element in that array. From the pseudo-code in Fig. 2.44, function lvalue calls rvalue(z) to generate instructions, if needed, to compute the r-value of z. It then constructs and returns a new Access node with children for the array name y and the r-value of z.

Expr lvalue(x : Expr) {

if ( x is an Id node ) return x;

else if ( x is an Access (y, z) node and y is an Id node ) {

return n e w Access(y, rvalue(z));

}

} else error;

 Figure 2.44: Pseudocode for function lvalue

Example2 . 19: When node x represents the array access a [2 *k], the call lvalue(x) generates an instruction

 t = 2 * k

and returns a new node x' representing the /-value a [ t ] , where t is a new temporary name.

In detail, the code fragment

 return new Access(y, rvalue(z));

is reached with y being the node for a and z being the node for expression 2*k. The cail rvalue(z) generates code for the expression 2*k (i.e., the three-address statement t = 2 * k) and returns the new node z' representing the temporary name t. That node z' becomes the value of the second field in the new Access node x' that is created. •

Expr rvalue(x : Expr) {

if ( x is an Id or a Constant node ) return x;

else if ( x is an Op(op,y,z) or a Rel(op,y,z) node ) {

 t = new temporary;

 emit string for t = rvalue(y) op rvalue(z);

 return a new node for t;

}

else if ( x is an Access (y,z) node ) {

 t — new temporary;

 call lvalue(x), which returns Access(y, z');

 emit string for t = Access(y, z')\

} return a new node for t;

else if ( x is an Assign (y, z) node ) {

 z' = rvalue(z)]

 emit string for lvalue(y) = z';

return z';

}

}

Figure 2.45: Pseudocode for function rvalue

Function rvalue in Fig. 2.45 generates instructions and returns a possibly new node. When x represents an identifier or a constant, rvalue returns x itself. In all other cases, it returns an Id node for a new temporary t. The cases are as follows:

• When x represents y op z, the code first computes y' = rvalue(y) and z' = rvalue(z). It creates a new temporary t and generates an instruction t = y' op z' (more precisely, an instruction formed from the string representations of t, y', op, and z'). It returns a node for identifier t.

• When x represents an array access ylz], we can reuse function lvalue.

The call lvalue(x) returns an access y [ 2 ' ] , where z' represents an identifier holding the offset for the array access. The code creates a new temporary t, generates an instruction based on t = y tz'l, and returns a node for t.

• When x represents y = z, then the code first computes z' = rvalue(z). It generates an instruction based on lvalue(y) = z' and returns the node z'.

Example 2 . 2 0 : When applied to the syntax tree for

a [ i ] = 2 * a [ j - k ]

function rvalue generates

t3 = j - k

t2 = a [ t3 ]

tl = 2 * t2

a [ i ] = tl

That is, the root is an Assign node with first argument a [ i ] and second ar-gument 2 * a [ j - k ] . Thus, the third case applies, and function rvalue recursively evaluates 2 * a [ j - k ] . The root of this subtree is the Op node for *, which causes a new temporary tl to be created, before the left operand, 2 is evaluated, and then the right operand. The constant 2 generates no three-address code, and its r-value is returned as a Constant node with value 2.

The right operand a [ j - k ] is an Access node, which causes a new temporary t2 to be created, before function lvalue is called on this node. Recursively, rvalue is called on the expression j -k. As a side-effect of this call, the three- address statement t3 = j - k is generated, after the new temporary t3 is created. Then, returning to the call of lvalue on a [ j - k ] , the temporary t2 is assigned the r-value of the entire access-expression, that is, t2 = a [ t3 ]. 

Now, we return to the call of rvalue on the Op node 2 * a [ j - k ] , which earlier created temporary t l . A three-address statement 11 = 2 * 12 is generated as a side-effect, to evaluate this multiplication-expression. Last, the call to rvalue on the whole expression completes by calling lvalue on the left side a [ i ] and then generating a three-address instruction a [ i ] = t l , in which the right side of the assignment is assigned to the left side. •

Better Code for Expressions

We can improve on function rvalue in Fig. 2.45 and generate fewer three-address instructions, in several ways:

                 Reduce the number of copy instructions in a subsequent optimization phase. For example, the pair of instructions t = i+1 and i = t can be

combined into i = i+1, if there are no subsequent uses of t.

• Generate fewer instructions in the first place by taking context into ac-count. For example, if the left side of a three-address assignment is an array access a [ t ] , then the right side must be a name, a constant, or a temporary, all of which use just one address. But if the left side is a name x, then the right side can be an operation y op z that uses two addresses.

We can avoid some copy instructions by modifying the translation functions to generate a partial instruction that computes, say j+k, but does not commit to where the result is to be placed, signified by a null address for the result:

The null result address is later replaced by either an identifier or a temporary, as appropriate. It is replaced by an identifier if j+k is on the right side of an assignment, as in i=j+k;, in which case (2.8) becomes

i  =  j                                       +  k

But, if j+k is a subexpression, as in j+k+1, then the null result address in (2.8) is replaced by a new temporary t, and a new partial instruction is generated

t = j + k null = t + 1

Many compilers make every effort to generate code that is as good as or bet-ter than hand-written assembly code produced by experts. If code-optimization techniques, such as the ones in Chapter 9 are used, then an effective strategy may well be to use a simple approach for intermediate code generation, and rely on the code optimizer to eliminate unnecessary instructions.

5. Exercises for Section 2.8

Exercise 2 . 8 . 1 :  For-statements in C and Java have the form:

for  (  expr_x                ;  expr₂   ;      expr₃         )        stmt

The first expression is executed before the loop; it is typically used for initializ-ing the loop index. The second expression is a test made before each iteration of the loop; the loop is exited if the expression becomes 0. The loop itself can be thought of as the statement {stmt expr₃;}. The third expression is executed at the end of each iteration; it is typically used to increment the loop index. The meaning of the for-statement is similar to

expr_±;                     while (  expr₂   )               {stmt  expr3;        }

Define a class For for for-statements, similar to class / / i n Fig. 2.43.

Exercise 2 . 8 . 2 : The programming language C does not have a boolean type. Show how a C compiler might translate an if-statement into three-address code.