Chapter: Compilers : Principles, Techniques, & Tools : A Simple Syntax-Directed Translator
Parsing
Parsing
1 Top-Down Parsing
2 Predictive Parsing
3 When to Use e-Productions
4 Designing a Predictive Parser
5 Left Recursion
6 Exercises for Section 2.4
Parsing is the process of determining how a string of terminals can be
generated by a grammar. In discussing this problem, it is helpful to think of a
parse tree being constructed, even though a compiler may not construct one, in
practice. However, a parser must be capable of constructing the tree in
principle, or else the translation cannot be guaranteed correct.
This section introduces a parsing method called "recursive
descent," which can be used both to parse and to implement syntax-directed
translators. A com-plete Java program, implementing the translation scheme of
Fig. 2.15, appears in the next section. A viable alternative is to use a
software tool to generate a translator directly from a translation scheme. Section 4.9 describes such a tool — Yacc; it
can implement the translation scheme of Fig. 2.15 without modification.
For any context-free grammar there is a parser that takes at most 0 ( n 3 ) time
to parse a string of n terminals. But
cubic time is generally too expen-sive. Fortunately, for real programming
languages, we can generally design a grammar that can be parsed quickly. Linear-time
algorithms suffice to parse essentially all languages that arise in practice.
Programming-language parsers almost always make a single left-to-right scan
over the input, looking ahead one terminal at a time, and constructing pieces
of the parse tree as they go.
Most parsing methods fall into one of two classes, called the top-down and bottom-up methods. These terms refer to the order in which nodes in
the parse tree are constructed. In
top-down parsers, construction starts at the root and proceeds towards the
leaves, while in bottom-up parsers, construction starts at the leaves and
proceeds towards the root. The popularity of top-down parsers is due to the
fact that efficient parsers can be constructed more easily by hand using
top-down methods. Bottom-up parsing, however, can handle a larger class of
grammars and translation schemes, so software tools for generating parsers
directly from grammars often use bottom-up methods.
1. Top-Down Parsing
We introduce top-down parsing by considering a grammar that is
well-suited for this class of methods. Later in this section, we consider the
construction of top-down parsers in general. The grammar in Fig. 2.16 generates
a subset of the statements of C or Java. We use the boldface terminals if and
for for the keywords "if" and "for", respectively, to
emphasize that these character sequences are treated as units, i.e., as single
terminal symbols. Further, the terminal expr represents expressions; a more
complete grammar would use a nonterminal expr and have productions for
nonterminal expr. Similarly, other is a terminal representing other statement
constructs.
The top-down construction of a parse tree like the one in Fig. 2.17, is
done by starting with the root, labeled with the starting nonterminal stmt, and re-peatedly performing the
following two steps.
1. At node JV, labeled with nonterminal A, select one of the productions for A and construct children at N
for the symbols in the production body.
Find the next node at which a
subtree is to be constructed, typically the leftmost unexpanded nonterminal of
the tree.
For some grammars, the above steps can be implemented during a single
left-to-right scan of the input string. The current terminal being scanned in
the
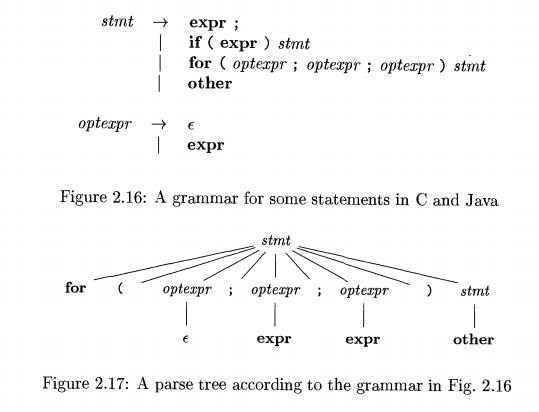
input is frequently referred to as the lookahead symbol. Initially, the lookahead symbol is the first,
i.e., leftmost, terminal of the input string. Figure 2.18 illustrates the
construction of the parse tree in Fig. 2.17 for the input string
for ( ; expr ; expr ) other
Initially, the terminal for
is the lookahead symbol, and the known part of the parse tree consists of the
root, labeled with the starting nonterminal stmt
in Fig. 2.18(a). The objective is to construct the remainder of the parse tree
in such a way that the string generated by the parse tree matches the input
string.
For a match to occur, the nonterminal stmt in Fig. 2.18(a) must derive a string that starts with the
lookahead symbol for. In the grammar
of Fig. 2.16, there is just one production for stmt that can derive such a string, so we select it, and construct
the children of the root labeled with the symbols in the production body. This
expansion of the parse tree is shown in Fig. 2.18(b).
Each of the three snapshots in Fig. 2.18 has arrows marking the lookahead
symbol in the input and the node in the parse tree that is being considered.
Once children are constructed at a node, we next consider the leftmost child.
In Fig. 2.18(b), children have just been constructed at the root, and the
leftmost child labeled with for is
being considered.
When the node being considered in the parse tree is for a terminal, and
the terminal matches the lookahead symbol, then we advance in both the parse
tree and the input. The next terminal in the input becomes the new lookahead
symbol, and the next child in the parse tree is considered. In Fig. 2.18(c),
the arrow in the parse tree has advanced to the next child of the root, and the
arrow
in the input has advanced to the next terminal, which is (. A further
advance will take the arrow in the parse tree to the child labeled with
nonterminal optexpr and take the
arrow in the input to the terminal ;.
At the nonterminal node labeled optexpr, we repeat the process of
selecting a production for a nonterminal. Productions with e as the body
("e-productions") require special treatment. For the moment, we use
them as a default when no other production can be used; we return to them in
Section 2.4.3. With nonterminal optexpr and lookahead ;, the e-production is used,
since ; does not match the only other production for optexpr, which has
terminal expr as its body.
In general, the selection of a production for a nonterminal may involve
trial-and-error; that is, we may have to try a production and backtrack to try
another production if the first is found to be unsuitable. A production is
unsuitable if, after using the production, we cannot complete the tree to match
the input string. Backtracking is not needed, however, in an important special
case called predictive parsing, which we discuss next.
2. Predictive Parsing
Recursive-descent parsing is a top-down method of syntax analysis in which a set of recursive procedures is used to process the input. One
procedure is associated with each nonterminal of a grammar. Here, we consider a
simple form of recursive-descent parsing, called predictive parsing, in which the lookahead symbol unambiguously
determines the flow of control through the procedure body for each nonterminal.
The sequence of procedure calls during the analysis of an input string implicitly defines a parse tree for the
input, and can be used to build an explicit
parse tree, if desired.
The predictive parser in Fig. 2 .
1 9 consists of procedures for the nontermi-nals stmt and optexpr of the
grammar in Fig. 2 . 1 6 and an
additional procedure match, used to
simplify the code for stmt and optexpr. Procedure match(t) com-pares its argument t with the lookahead symbol and advances to the next input terminal
if they match. Thus match changes the
value of variable lookahead, a global
variable that holds the currently scanned input terminal.
Parsing begins with a call of the procedure for the starting nonterminal
stmt. With the same input as in Fig. 2 . 1 8 , lookahead is initially the first terminal for. Procedure stmt
executes code corresponding to the production
stmt ->• for (
optexpr ; optexpr ; optexpr ) stmt
In the code for the production body — that is, the for case of procedure stmt —
each terminal is matched with the lookahead symbol, and each nonterminal leads
to a call of its procedure, in the following sequence of calls:
match(for); matched);
optexprQ; match(';'); optexprQ; match(';'); optexprQ;
match(')'); stmt();
Predictive parsing relies on information about the first symbols that
can be generated by a production body. More precisely, let a be a string of grammar symbols (terrninals and/or nonterminals).
We define F I R S T ( a ) to be the
set of terminals that appear as the first symbols of one or more strings of
terminals generated from a. If a is e or can generate e, then e is also in F I
R S T (a).
The details of how one computes FIRST ( o ;) are in Section 4 . 4 . 2 .
Here, we shall just use ad hoc reasoning to deduce the symbols in F I R S T
(a); typically, a will either begin with a terminal, which is therefore the
only symbol in F I R S T ( Q ; ) , or a will begin with a nonterminal whose
production bodies begin with termi-nals, in which case these terminals are the
only members of F I R S T ( a ) .
For example, with respect to the grammar of Fig. 2 . 1 6 , the following
are correct calculations of FIRST.


3. When to Use e-Productions
Our predictive parser uses an e-production as a default when no other
produc-tion can be used. With the input of Fig. 2.18, after the terminals for and ( are matched, the lookahead
symbol is ;. At this point procedure optexpr
is called, and the code
if ( lookahead === expr ) match (expr);
in its body is executed. Nonterminal optexpr
has two productions, with bodies expr and
e. The lookahead symbol ";" does not match the terminal expr, so the production with body expr
cannot apply. In fact, the procedure returns without changing the lookahead
symbol or doing anything else. Doing nothing corresponds to applying an
e-production.
More generally, consider a variant of the productions in Fig. 2.16 where
optexpr generates an expression
nonterminal instead of the terminal expr:

Thus, optexpr either generates an
expression using nonterminal expr or it generates e. While parsing
optexpr, if the lookahead symbol is not in FIRST (espr), then the e-production
is used.
For more on when to use e-productions, see the discussion of LL(1)
grammars in Section 4.4.3.
4. Designing
a Predictive Parser
We can generalize the technique introduced informally in Section 2.4.2,
to apply to any grammar that has disjoint FIRST sets for the production bodies
belonging to any nonterminal. We shall also see that when we have a translation
scheme — that is, a grammar with embedded actions — it is possible to execute
those actions as part of the procedures designed for the parser.
Recall that a predictive parser
is a program consisting of a procedure for every nonterminal. The procedure for
nonterminal A does two things.
1. It decides which A-production to use by examining the lookahead
symbol. The production with body a
(where a is not e, the empty string)
is used if the lookahead symbol is in F i R S T ( a ) . If there is a conflict
between two nonempty bodies for any lookahead symbol, then we cannot use this
parsing method on this grammar. In addition, the e-production for A, if it exists, is used if the
lookahead symbol is not in the FIRST set for any other production body for A.
2. The procedure then mimics the body of the chosen production. That is,
the symbols of the body are "executed" in turn, from the left. A
nonterminal is "executed" by a call to the procedure for that
nonterminal, and a terminal matching the lookahead symbol is
"executed" by reading the next input symbol. If at some point the
terminal in the body does not match the lookahead symbol, a syntax error is
reported.
Figure 2.19 is the result of applying these rules to the grammar in Fig.
2.16.
Just as a translation scheme is formed by extending a grammar, a
syntax-directed translator can be formed by extending a predictive parser. An
algo-rithm for this purpose is given in Section 5.4. The following limited
construction suffices for the present:
Construct a predictive parser,
ignoring the actions in productions.
Copy the actions from the
translation scheme into the parser. If an action appears after grammar symbol X in production p, then it is copied after the implementation of X in the code for p. Otherwise, if it appears at the beginning of the production,
then it is copied just before the code for the production body.
We shall construct such a translator in Section 2.5.
5. Left Recursion
It is possible for a recursive-descent parser to loop forever. A problem
arises with "left-recursive" productions like
expr —y expr + term
where the leftmost symbol of the body is the same as the nonterminal at
the head of the production. Suppose the procedure for expr decides to apply this production. The body begins with expr so the procedure for expr is called recursively. Since the
lookahead symbol changes only when a terminal in the body is matched, no change
to the input took place between recursive calls of expr. As a result, the second call to expr does exactly what the first call did, which means a third call to expr,
and so on, forever.
A left-recursive production can be eliminated by rewriting the offending
production. Consider a nonterminal A
with two productions
A
->• Aa | /3
where a and /3 are sequences of terminals and
nonterminals that do not start with A.
For example, in
expr —y expr + term \ term
nonterminal A — expr, string a = + term, and string (3 = term.
The nonterminal A and its
production are said to be left recursive,
because the production A -> Aa has
A itself as the leftmost symbol on
the right side.4 Repeated application of this production builds up a sequence of a's to
the right of A, as in Fig. 2.20(a).
When A is finally replaced by /3, we have a /3 followed by a sequence of zero or more a's .
The same effect can be achieved, as in Fig. 2.20(b), by rewriting the
productions for A in the following manner, using a new nonterminal R:
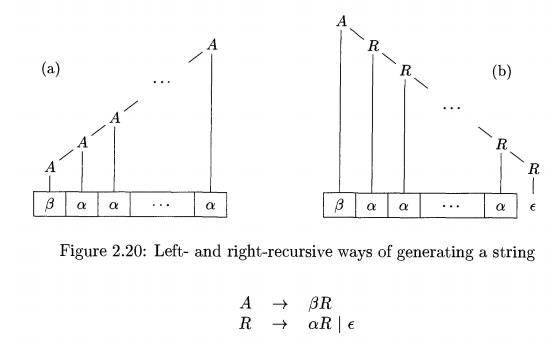
Nonterminal R and its production R -» aR are recursive because this pro duction for R has R itself as the last symbol on the right side. Right-recursive
productions lead to trees that grow down towards the right, as in Fig. 2.20(b).
Trees growing down to the right make it harder to translate expressions
con-taining left-associative operators, such as minus. In Section 2.5.2,
however, we shall see that the proper translation of expressions into postfix
notation can still be attained by a careful design of the translation scheme.
In Section 4.3.3, we shall consider more general forms of left recursion
and show how all left recursion can be eliminated from a grammar.
6. Exercises for Section 2.4
Exercise 2 . 4 . 1 : Construct
recursive-descent parsers, starting with the following grammars:
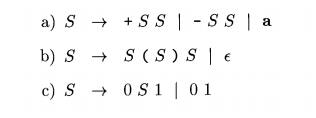
Related Topics