A Translator for Simple Expressions

A Translator for Simple Expressions

1 Abstract and Concrete Syntax

2 Adapting the Translation Scheme

3 Procedures for the Nonterminals

4 Simplifying the Translator

5 The Complete Program

Using the techniques of the last three sections, we now construct a syntax-directed translator, in the form of a working Java program, that translates arithmetic expressions into postfix form. To keep the initial program manage-ably small, we start with expressions consisting of digits separated by binary plus and minus signs. We extend the program in Section 2.6 to translate ex-pressions that include numbers and other operators. It is worth studying the translation of expressions in detail, since they appear as a construct in so many languages.

A syntax-directed translation scheme often serves as the specification for a translator. The scheme in Fig. 2.21 (repeated from Fig. 2.15) defines the translation to be performed here.

Often, the underlying grammar of a given scheme has to be modified before it can be parsed with a predictive parser. In particular, the grammar underlying the scheme in Fig. 2.21 is left recursive, and as we saw in the last section, a predictive parser cannot handle a left-recursive grammar.

We appear to have a conflict: on the one hand we need a grammar that facilitates translation, on the other hand we need a significantly different gram-mar that facilitates parsing. The solution is to begin with the grammar for easy translation and carefully transform it to facilitate parsing. By eliminating the left recursion in Fig. 2.21, we can obtain a grammar suitable for use in a predictive recursive-descent translator.

1. Abstract and Concrete Syntax

A useful starting point for designing a translator is a data structure called an abstract syntax tree. In an abstract syntax tree for an expression, each interior node represents an operator; the children of the node represent the operands of the operator. More generally, any programming construct can be handled by making up an operator for the construct and treating as operands the semantically meaningful components of that construct.

In the abstract syntax tree for 9 - 5 + 2 in Fig. 2.22, the root represents the operator +. The subtrees of the root represent the subexpressions 9 - 5 and 2. The grouping of 9 - 5 as an operand reflects the left-to-right evaluation of operators at the same precedence level. Since - and + have the same precedence, 9 - 5 + 2 is equivalent to ( 9 - 5 ) + 2 .

Abstract syntax trees, or simply syntax trees, resemble parse trees to an extent. However, in the syntax tree, interior nodes represent programming constructs while in the parse tree, the interior nodes represent nonterminals. Many nonterminals of a grammar represent programming constructs, but others are "helpers" of one sort of another, such as those representing terms, factors, or other variations of expressions. In the syntax tree, these helpers typically are not needed and are hence dropped. To emphasize the contrast, a parse tree is sometimes called a concrete  syntax tree,  and the underlying grammar is called a  concrete  syntax for the  language.

In the syntax tree in Fig.  2.22,  each interior node is associated with an operator,  with  no "helper"  nodes  for  single  productions  (a production  whose body consists of a single nonterminal, and nothing else) like expr —»• term or for e-productions like rest -> e.

It is desirable for a translation scheme to be based on a grammar whose parse trees are as close to syntax trees as possible. The grouping of subexpressions by the grammar in Fig. 2.21 is similar to their grouping in syntax trees. For example, subexpressions of the addition operator are given by expr and term in the production body expr+ term.

2. Adapting the Translation Scheme

The left-recursion-elimination technique sketched in Fig. 2.20 can also be ap-plied to productions containing semantic actions. First, the technique extends to multiple productions for A. In our example, A is expr, and there are two left-recursive productions for expr and one that is not left recursive. The technique transforms the productions 

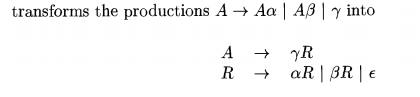
Second, we need to transform productions that have embedded actions, not just terminals and nonterminals. Semantic actions embedded in the productions are simply carried along in the transformation, as if they were terminals.

Example 2 . 1 3 :  Consider the translation scheme of Fig. 2.21.  Let

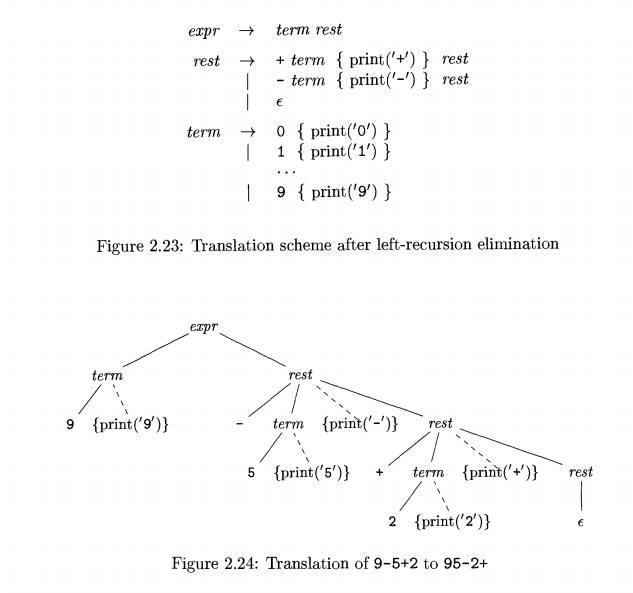
Then the left-recursion-eliminating transformation produces the translation scheme in Fig. 2.23. The expr productions in Fig. 2.21 have been transformed into the productions for expr, and a new nonterminal rest plays the role of R.

The productions for term are repeated from Fig. 2.21.  Figure 2.24 shows how 9-5+2 is translated using the grammar in Fig. 2.23. •

Left-recursion elimination must be done carefully, to ensure that we preserve the ordering of semantic actions. For example, the transformed scheme in Fig. 2.23 has the actions { print ('+') } and { print(' - ') } in the middle of a production body, in each case between nonterminals term and rest. If the actions were to be moved to the end, after rest, then the translations would become incorrect. We leave it to the reader to show that 9-5+2 would then be translated incorrectly into 952+-, the postfix notation for 9-(5+2), instead of the desired 95-2+, the postfix notation for (9-5)+2.

3. Procedures for the Nonterminals

Functions expr, rest, and term in Fig. 2.25 implement the syntax-directed trans-lation scheme in Fig. 2.23. These functions mimic the production bodies of the  corresponding nonterminals.  Function  expr implements  the  production expr ->  term  rest by the calls term() followed  by  rest().

Function rest implements the three productions for nonterminal rest in Fig. 2.23. It applies the first production if the lookahead symbol is a plus sign, the second production if the lookahead symbol is a minus sign, and the production rest e in all other cases. The first two productions for rest are implemented by the first two branches of the if-statement in procedure rest. If the lookahead symbol is +, the plus sign is matched by the call match('+'). After the call term(), the semantic action is implemented by writing a plus character. The second production is similar, with - instead of +. Since the third production for rest has e as its right side, the last else-clause in function rest does nothing.

The ten productions for term generate the ten digits. Since each of these productions generates a digit and prints it, the same code in Fig. 2.25 imple-ments them all. If the test succeeds, variable t saves the digit represented by lookahead so it can be written after the call to match. Note that match changes the lookahead symbol, so the digit needs to be saved for later printing.⁵

4. Simplifying the Translator

Before showing a complete program, we shall make two simplifying transfor-mations to the code in Fig. 2.25. The simplifications will fold procedure rest into procedure expr. When expressions with multiple levels of precedence are translated, such simplifications reduce the number of procedures needed.

First, certain recursive calls can be replaced by iterations. When the last statement executed in a procedure body is a recursive call to the same proce-dure, the call is said to be tail recursive. For example, in function rest, the calls of rest() with lookahead + and - are tail recursive because in each of these branches, the recursive call to rest is the last statement executed by the given call of rest.

For a procedure without parameters, a tail-recursive call can be replaced simply by a jump to the beginning of the procedure. The code for rest can be rewritten as the pseudocode of Fig. 2.26. As long as the lookahead symbol is a plus or a minus sign, procedure rest matches the sign, calls term to match a digit, and continues the process. Otherwise, it breaks out of while loop and returns from  rest.

Second, the complete Java program will include one more change. Once the tail-recursive calls to rest in Fig. 2.25 are replaced by iterations, the only remaining call to rest is from within procedure expr. The two procedures can therefore be integrated into one, by replacing the call restQ by the body of procedure rest.

5. The Complete Program

The complete Java program for our translator appears in Fig. 2.27. The first line of Fig. 2.27, beginning with import, provides access to the package j ava. io for system input and output. The rest of the code consists of the two classes Parser and Postfix. Class Parser contains variable lookahead and functions

 Parser, expr, term, and match.

Execution begins with function main, which is defined in class Postfix. Function main creates an instance parse of class Parser and calls its function expr to parse an expression.  

The function Parser, with the same name as  its class,  is a  constructor, it is called automatically when an object of the class is created. Notice from its definition at the beginning of class Parser that the constructor Parser initializes variable lookahead by reading a token. Tokens, consisting of single characters, are supplied by the system input routine read, which reads the next character from the input file. Note that lookahead is declared to be an integer, rather than a character, to anticipate the fact that additional tokens other than single characters will be introduced in later sections.

Function expr is the result of the simplifications discussed in Section 2.5.4; it implements nonterminals expr and rest in Fig. 2.23. The code for expir in Fig. 2.27 calls term and then has a while-loop that forever tests whether lookahead matches either ' + ' or ' - ' . Control exits from this while-loop when it reaches the return statement. Within the loop, the input/output facilities of the System class are used to write a character.

Function term uses the routine isDigit from the Java class Character to test if the lookahead symbol is a digit.  The routine  isDigit expects to be applied to a character; however, lookahead is declared to be an integer, anticipating future extensions. The construction (char) lookahead casts or coerces lookahead to be a character. In a small change from Fig. 2.25, the semantic action of writing the lookahead character occurs before the call to match.

The function match checks terminals; it reads the next input terminal if the lookahead symbol is matched and signals an error otherwise by executing  throw new  Error("syntax error");

This  code creates a new exception of class Error and supplies it the string syntax error as an error message. Java does not require Error exceptions to be declared in a throws clause, since they are meant to be used only for abnormal events that should never occur.6 6 Error handling can be streamlined using the exception-handling facilities of Java. One ap-proach is to define a new exception, say SyntaxError, that extends the system class Exception. Then, throw SyntaxError instead of Error when an error is detected in either term or match. Further, handle the exception in main by enclosing the call parse.expr() within a try state-ment that catches exception SyntaxError, writes a message, and terminates. We would need to add a class SyntaxError to the program in Fig. 2.27. To complete the extension, in addition to IOException, functions match and term must now declare that they can throw SyntaxError. Function expr, which calls them, must also declare that it can throw SyntaxError.

A Few Salient Features of Java

Those unfamiliar with Java may find the following notes on Java helpful in reading the code in Fig. 2.27:

                          A class in Java consists of a sequence of variable and function defi-nitions.

                          Parentheses enclosing function parameter lists are needed even if there are no parameters; hence we write expr() and term(). These functions are actually procedures, because they do not return values, signified by the keyword void before the function name.

• Functions communicate either by passing parameters "by value" or by accessing shared data. For example, the functions expr() and term() examine the lookahead symbol using the class variable lookahead that they can all access since they all belong to the same class Parser.

            Like C, Java uses = for assignment, == for equality, and != for in-equality.

            The clause "throws IOException" in the definition of term() de-clares that an exception called IOException can occur. Such an exception occurs if there is no input to be read when the function match uses the routine read. Any function that calls match must also declare that an IOException can occur during its own execution.