Symmetry through transformations

Symmetry through transformations

We learnt the types of symmetry. Now we are going to learn symmetry of figures through transformations.

Transformation describe how geometric figures of the same shape are related to one another. Figures or shapes in a plane can be translated, reflected or rotated to get new figures.

The original figure is called the pre-image and the new figure is called the image. Pre-images are denoted by A, B, C … etc., and the images are denoted by A', B', C', … etc. A' can be read as A prime.

Leonardo da Vinci’s Vitruvian Man (ca. 1487) is often used as a representation of symmetry in the human body and, by extension, the natural universe.

The operation that maps or moves the pre-image onto the image is called the transformation.

A transformation is a specific set of rules that change the pre-image onto the image.

In this chapter we are going to learn three types of transformation.

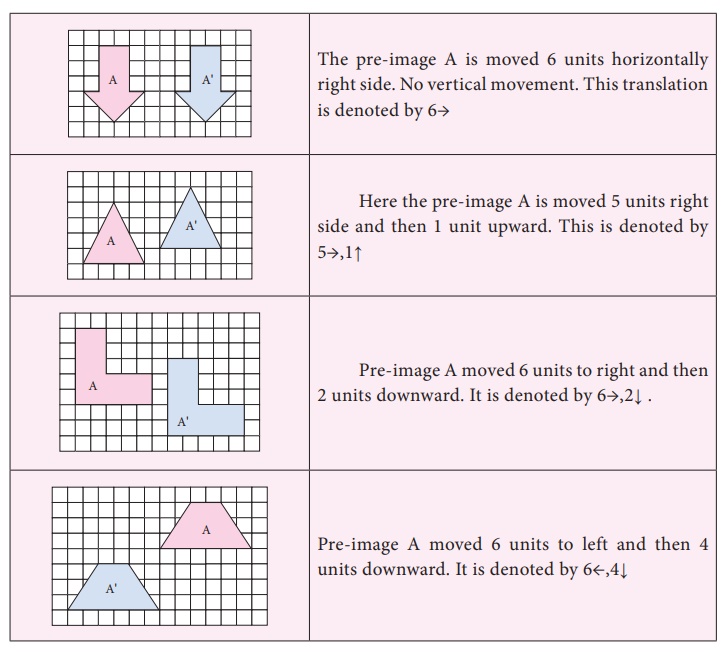
1. Translation:

A translation is a transformation that moves all points of a figure in the same distance in the same direction.

Look at the Fig 4.8.

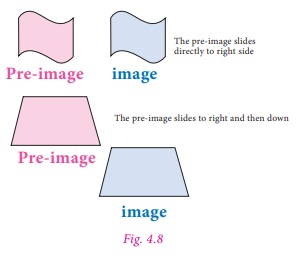
From these examples we can observe that all points of a figure move in the same distance and in the same direction.

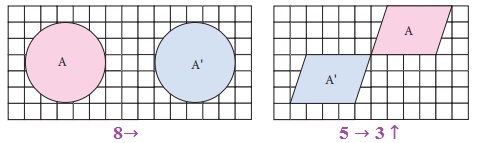
Using a grid paper, we can specify a translation by how far the shape is moved horizontally and then vertically.

In horizontal, the right side movement is denoted by → and the left side  movement is denoted ←.

In vertical, the upside movement is denoted ↑ and the downward movement is denoted ↓.

TRY THESE

1. Translate this figure to 4 → 3 ↑

Solution:  

2. Translate this figure to 2 ↓ 1 ←

Solution:

3. How is the pre–image A translated to image A’ in each of the following figures?

Solution:

8→

5 → 3 ↑

Think

The pre-image and the image after a translation coincide. What can you say about the translation?

Solution:  There is no right, left, up or down movement took place.

Activity

Here is a letter grid. Start with Square A. From A move 5 units right then 2 units down and stop. Then move 3 units left then 2 units up and stop. What mathematical word you get? Start at square L. Move 3 units left and stop. Then move 1 unit left and 1 unit down and stop. Then move 3 units right then 2 unit up and stop. What mathematical word you get? Give instruction to get (i) Right (ii) Angle (iii) Work (iv) Hard

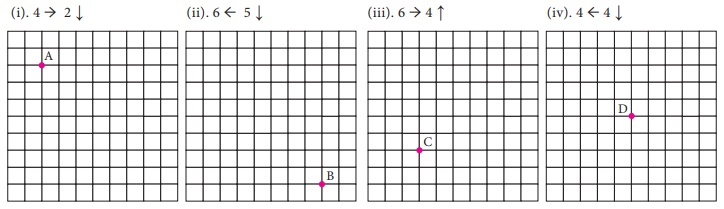
Example 4.1

 Find the new position of each point using the translation given.

(i). 4 → 2 ↓

(ii). 6 ← 5 ↓

(iii). 6 → 4 ↑

 (iv). 4 ← 4 ↓

Solution:

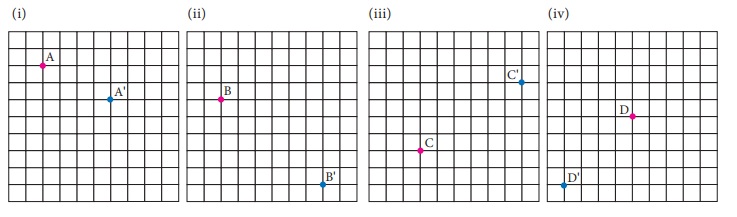
Example 4.2

How is the pre-image translated to the image?

Solution:

(i) A is translated to A’ by 5→,2↑

(ii) B is translated to B’ by 5←,3↑

(iii) C is translated to C’ by 4←,5↓

The sights and pageantry of marching band performance can add to the excitement of a sporting event. Band members dedicate a lot of time and energy to learning the music as well as the movements required for a performance.

The movements of each band member as they progress throughout the show are examples of translations.

2. Reflection

A reflection is a transformation that “flips” or “reflects” a figure about a line.

After a figure is reflected, it looks like a mirror image of itself. The line that a figure is flipped over is called a line of reflection.

We can observe reflection in water, a mirror or in a glossy surface as shown in Fig. 4.9.

Observe the following pictures.

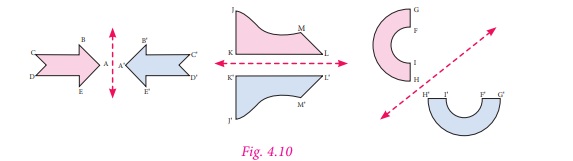
In the above pictures (Fig. 4.10), the figures are reflected by a line. This line is called a line of reflection. Here the red line is the line of reflection.

We can observe that the figures and its reflections are exactly the same distance from the line of reflection on both sides.

The line of reflection may be horizontal or vertical or slanting and also it may be on the shape or outside the shape.

Note

The line of reflection is the perpendicular bisector of the line joining at any point and its image

How to reflect a shape about a line?

To reflect the shape about the line of reflection, we have to reflect every vertex individually and then connect them again.

First, choose one of the vertices and draw the line through this vertex so that it is perpendicular to the line of reflection.

Now measure the distance from the vertex to the line of the reflection, and mark a point that has the same distance on the other side. It can be done by using either a ruler or a compass.

Repeat the process for all the other vertices of the shape.

Finally connect all the reflected vertices in the correct order to get the reflection of the shape.

Try these

1. Draw the line of reflection in the following pictures.

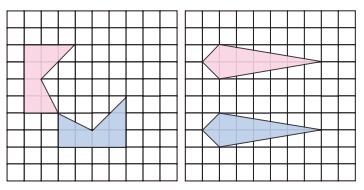
Solution: 

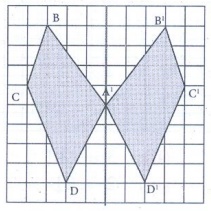
2. Reflect the shape with given line of reflection.

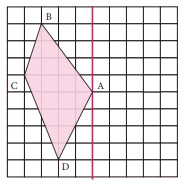
Solution: 

Taj Mahal at Agra is planned by following the axis with Bilateral symmetrical design in plan and overall campus as the mirror image as shown in figure.

The symmetry in architecture is implied by its axiality or centrality in the form of the building. The monumental architecture often uses symmetrical design i.e. mirrored, which show stability, balance and control.

Example 4.3

 Reflect the shape in each of the following pictures with given line of reflection.

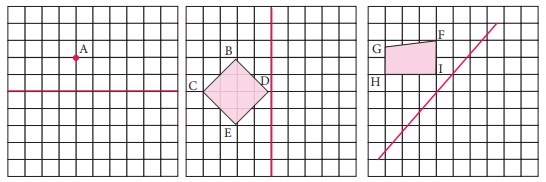
Solution:

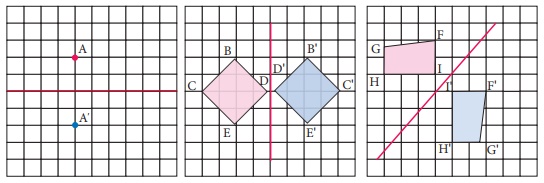
Example 4.4

 Reflect the letter about the red line.

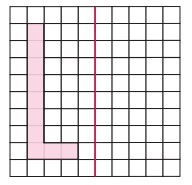
Solution:

3. Rotation

A rotation is a transformation that turns every point of the pre-image through a specified angle and direction about a point.

The fixed point is called the centre of rotation. The angle is called the angle of rotation. A rotation is also called a turn.

The default direction of a rotation is the anti-clockwise direction. The angle of rotation can be any value between 0 and 360 degrees, both are included.

Rotation of 360° is called a full turn, rotation of 180° is called a half turn, rotation of 90° is called a quarter turn.

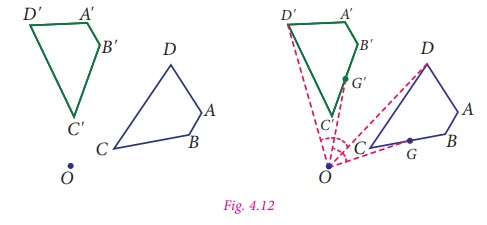
In Fig. 4.12 the preimage ABCD is rotated about the point O to get the image A’B’C’D’. Here the angles ∠AOA’, ∠BOB’, ∠COC’, ∠DOD’ are equal. Any point G on the preimage ABCD will have a corresponding image G’ on A’B’C’D’ such that ∠GOG’ = ∠AOA’ = ∠BOB’ = ∠COC’ = ∠DOD’ which is the angle of rotation.

Activity

● Fold a piece of paper and lable it as shown. Cut scalene triangle out of the folded paper and unfold the paper. You can see triangles in all three parts How are the triangles in parts 2 and 3 are related to triangle in part 1?

● Fold a piece of paper and lable it as shown. Cut scalene triangle out of the folded paper and unfold the paper. You can see triangles in all four parts. How are the triangles in part 2, part 3 and part 4 are related to triangle in part 1?

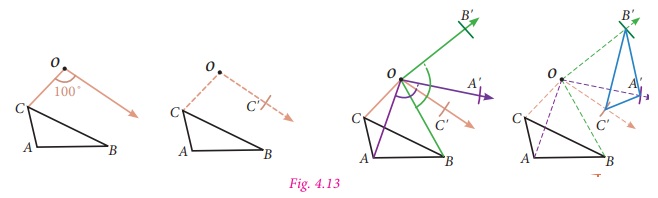
How to rotate a shape about a point?

To rotate a shape about a point with the given angle, we have to rotate every vertex individually and connect them again.

Here ΔABC is rotated about O with angle of 100°.

Step1. Draw CO. Make angle of 100° with vertex C and side CO using a protractor.

Step2. Use a compass to construct CO’ = CO

Step3. Locate A’ and B’ in the similar way.

Step4. Join A’, B’, C’ to form ΔA’B’C’

Note

A 180° clockwise rotation and a 180° counter clockwise rotation have the same image.,So, you do not need to specify direction when rotating a figure 180°.

Example 4.5

Rotate the pink point about the green point by given angle of rotation and direction

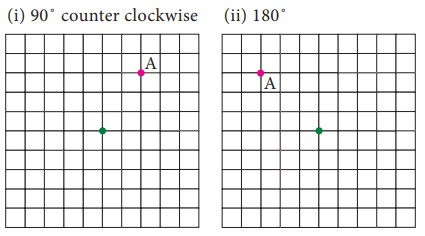
Solution:

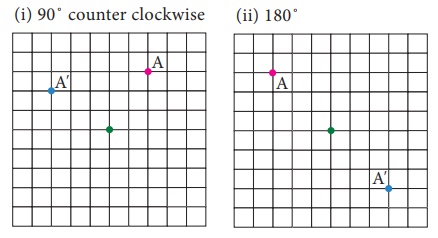
Example 4.6

Rotate the pink shape about the green point by given angle of rotation and direction

(i) 180˚ (ii) 90˚ counter clockwise

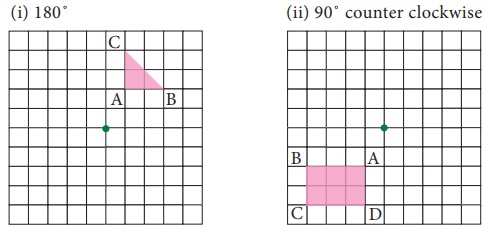
Solution:

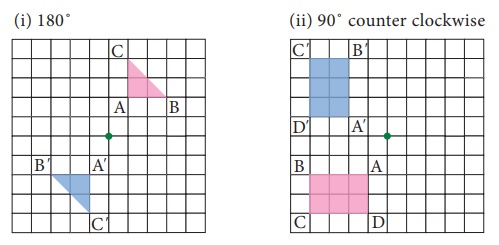
Example 4.7

Describe the transformation involved in the following pair of figures. Write translation, reflection or rotation.

Solution:

(i) Reflection (ii) Rotation (iii) Translation

A glide reflection is a combination of two transformations: a reflection about a line and a translation. Here the translation is parallel to the line of reflection. Reversing the order of the composition will not affect the outcome. We can translate first and then reflect, or reflect first and then translate.