Chapter: Digital Electronics : Minimization Techniques and Logic Gates
Sum-of-Products (SOP) Form
SUM-OF-PRODUCTS (SOP) FORM:
Two or more product terms summed by Boolean addition
Any expression -> SOP using Boolean algebra
Example:
A + BC
Sum-of-Products (SOP) Form:
*AB+ B(CD + EF) = AB+ BCD + BEF
*(A + B)(B + C + D) = AB+ AC+ AD+ B + BC + BD
= AC + AD + B
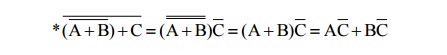
Implementation of SOP Expression by using basic gates
B+AC+AD
CANONICAL FORM:
In SOP and POS, if all the term contains all the variables either in true or in complementary form then its said to be canonical SOP or canonical POS.
2. MINTERM ( canonical SOP)
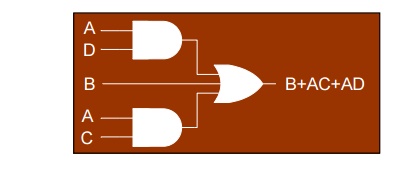
In a Boolean function, a binary variable (x) may appear either in its normal form (x) or in its complement form (x’).Consider 2 binary variables x and y and an AND operation, there are 4 and only 4 possible combinations: x’•y’, x’•y, x•y’ & x•y.
Each of the 4 product terms is called a MINTERM or STANDARD PRODUCT
By definition, a Minterm is a product which consists of all the variables in the normal form or the complement form but NOT BOTH.
e.g. for a function with 2 variables x and y: x•y’ is a minterm but x’ is NOT a minterm
e.g. for a function with 3 variables x, y andz:
x’yz’ is a minterm but xy’ is NOT a minterm
3. MAXTERM (canonical POS)
Consider 2 binary variables x and y and an OR operation, there are 4 and only 4 possible combinations: x’+y’, x’+y, x+y’, x+y.Each of the 4 sum terms is called a MAXTERM or STANDARD SUM.By definition, a Maxterm is a sum in which each variable appears once and only once either in its normal form or its complement form but NOT BOTH.
Minterms and Maxterms for 3 Variables
Minterm Boolean Expression
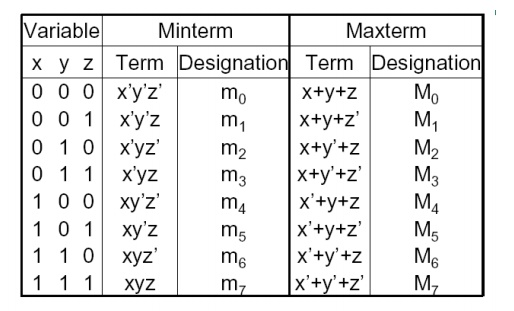
Boolean functions can be expressed with minterms,
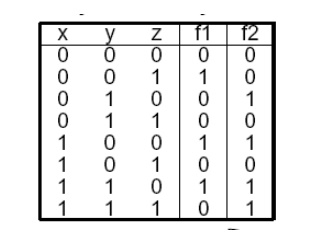
e.g.f1(x,y,z) = m1 + m4 + m6 = ÎŁm(1, 4, 6)
f2(x,y,z) = m2 + m4 + m6+ m7
= ÎŁm(2, 4, 6, 7)
Maxterm Boolean Expression
Boolean functions can also be expressed with maxterms,
e.g.f1’ = x’y’z’+x’yz’+x’yz+xy’z+xyz
f1 = (x’y’z’+x’yz’+x’yz+xy’z+xyz)’
= (x+y+z)(x+y’+z)(x+y’+z’)(x’+y+z’)(x’+y’+z’)
= M0•M2•M3•M5•M7
= Î M(0, 2, 3, 5, 7)
f2 = M0•M1•M3•M5 = ΠM(0, 1, 3, 5)
Express Boolean Functions in Minterms
If product terms in a Boolean function are not minterms, they can be converted to minterms
e.g. f(a,b,c) = a’ + bc’ + ab’c
Function f has 3 variables, therefore, each minterm must have 3 literals.
Neither a’ nor bc’ are minterms.They can be converted to minterm.ab’c is a minterm
Conversion to Minterms
e.g. f(a,b,c) = a’ + bc’ + ab’c
To convert a’ to a minterm, the 2 variables (b, c) must be added, without changing its functionality .Since a’=a’•1 & 1 = b+b’, a’= a’(b + b’) = a’b + a’b’
Similarly, a’b = a’b(c + c’) = a’bc + a’bc’ and a’b’ = a’b’(c+c’) = a’b’c + a’b’c’ bc’ = bc’(a+a’) = abc’ + a’bc’
f = a’bc+a’bc’+a’b’c+a’b’c’+abc’+a’bc’+ab’c
Express Boolean Functions in Maxterms
By using the Distribution Law: x+yz = (x+y)(x+z), a Boolean function can be converted to an expression in product of maxterms
e.g. f(a,b,c) = a’+bc’
= (a’+b)(a’+c’) {not maxterms}
= (a’+b+cc’)(a’+c’+bb’) {cc’=0}
= (a’+b+c)(a’+b+c’)(a’+c’+b)(a’+c’+b’)
= (a’+b+c)(a’+b+c’)(a’+c’+b’)
Boolean Function Manipulation
Boolean functions can be manipulated with Boolean algebra. Manipulation can transform logic expressions, but still keep the same logic functionality.Manipulation can reduce the complexity, hence, easier to be implemented in hardware, i.e. fewer logic gates
Boolean Function Manipulation Example
f = xy’ + xyz + x’z
= x(y’ + yz) + x’z {common factor}
= x[(y’+y)(y’+z)] + x’z {Distribution law}
= x(y’+z) + x’z {y’ + y = 1}
= xy’ + xz + x’z {Distribution law}
= xy’ + (x + x’)z {common factor}
= xy’ + z {x + x’ = 1}
Simplify f1=abc+a’b+abc’ and f2=(a+b)’(a’+b’) to the minimum literals
f1 = abc+a’b+abc’ = ab(c+c’) + a’b = ab + a’b = (a+a’)b = b
f2 =(a+b)’(a’+b’) = a’b’(a’+b’) {DeMorgan}
= a’b’a’+a’b’b’
= a’b’ + a’b’ = a’b’
Related Topics