Boolean Postulates and Laws

BOOLEAN POSTULATES AND LAWS:

T1 : Commutative Law

(a)        A + B = B + A

(b)       A B = B A

T2 : Associate Law

(a)        (A + B) + C = A + (B + C)

(b)       (A B) C = A (B C)

T3 : Distributive Law

(a)        A (B + C) = A B + A C

(b)       A + (B C) = (A + B) (A + C)

T4 : Identity Law

(a)        A + A = A

(b)       A A = A

T5 :

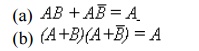
T6 : Redundance Law

(a)        A + A B = A

(b)       A (A + B) = A

T7 :

(a)        0 + A = A

(b)       0 A = 0

T8 :

(a)        1 + A = 1

(b)       1 A = A

T9 :

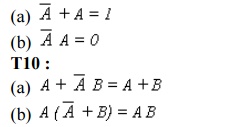
Boolean Theorems

Investigating the various Boolean theorems (rules) can help us to simplify logic expressions and logic circuits.

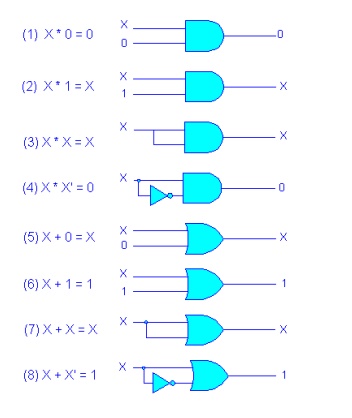
Boolean postulates are                   

— The Commutative Law of addition for two variable.       

         A + B         =       B + A         

— The Commutative Law of multiplication for two  variable.       

         A . B  =  B  . A   

— The Associative law of addition with multiplication is written as       

         A + (B + C) = A +B +C

— The Associative law of multiplication with addition is written as       

         A . (B . C)  = (A . B) . C        

— The Associative law of multiplication with addition is written as       

         A . (B + C)  =  A . B + A . C  

— The Associative law of addition with multiplication is written as       

         A + (B . C) = (A + B) . (A + C)