Chapter: Digital Electronics : Minimization Techniques and Logic Gates
Keeping Circuits Simple (Karnaugh Maps)
KEEPING CIRCUITS SIMPLE (KARNAUGH MAPS)
We have just seen how using the logic identities can simplify a Boolean expression. This is important because it reduces the number of gates needed to construct the logic circuit.
However, as I am sure you will agree, having to work out Boolean problems in longhand is not easy. It takes time and ingenuity HereŌĆÖs a basic outline showing how to apply Karnaugh mapping to a three-input system:
1. First, select a desired truth table.
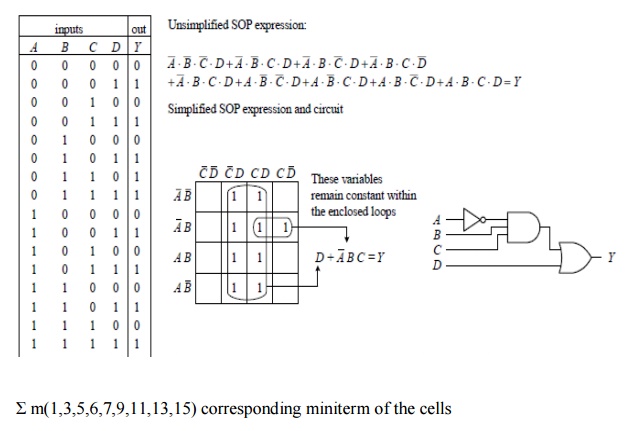
2. Next, translate the truth table into a Karnaugh map. AKarnaugh map is similar to a truth table but has its variables represented along two axes. Translating the truth table into a Karnaugh map reduces the number of 1s and 0s needed to present the information. Figure shows how the translation is carried out.
3. After you create the Karnaugh map, you proceed to encircle adjacent cells of 1s into groups of 2, 4, or 8. The more groups you can encircle, the simpler the final equation will be. In other words, take all possible loops.
4. Now, identify the variables that remain constant within each loop, and write out an SOP equation by ORing these variables together. Here,constant means that a variable and its inverse are not present together within the loop. For example, the top horizontal loop in Fig. yields A_B_ (the first term in the SOP expression), since A_ŌĆÖs and B_ŌĆÖs inverses (A and B) are not present. However, the C variable is omitted from this term because Cand C_ are both present.
5. The SOP expression you end up with is the simplest possible expression. With it you can create your logic circuit. You may have to apply some bubble pushing to make the final circuit practical, as shown in the figure below.
To apply Karnaugh mapping to four-input circuits, you apply the same basic steps used in the three-input scheme. However, now you use must use a 4 ├Ś 4 Karnaugh map to hold all the necessary information. Here is an example of how a four-input truth table (or unsimplified four-variable SOP expression) can be mapped and converted into a simplified SOP expression that can be used to create the final logic circuit:
Filling the cell with 1s from SOP form:
1 When output is 1 for a given combination of A, B and C, we place 1 at the corresponding cell.
2 Complete the step 1 for all the rows of truth table with outputs = 1.
Filling the cell with 0s from POS form:
1 When output is 0 for a given combination of A, B and C, we place 0 at the corresponding cell.
2 Complete the step 1 for all 8 rows of truth table with outputs = 0.
Map from 3 variables Truth table or SOP form Boolean Expression:
_ A two-dimensional map built from a truth table or 3 variables SOP form Boolean Expression _ Since number of rows in three variable (three inputs) truth table are 8, the map has 8 cells _ Two cells horizontal and four cells vertical. [It can also be vice versa.
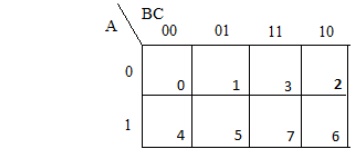
1.THREE VARIABLE KARNAUGHMAP:
Step 1:
Simplify the following Boolean functions, using three variable maps F(A,B,C) =
Ōłæ(0,2,3,6,7)?
┬Ę Draw the K-map diagram for three variable method.
┬Ę A three variable method contains 23 = 8 cells.
┬Ę Assign the three variable as A,B,C. for this method in K-map table value should be in 0 to 7 because its an three variable method.
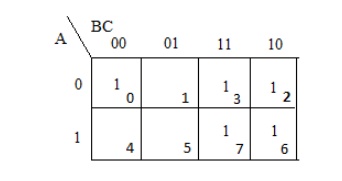
Step 2:
┬Ę From the given example enter the value ŌĆś1ŌĆÖ for given decimal value in K-map diagram.
Step 3:
┬Ę Check for those 1ŌĆÖs which are adjacent to only one other 1 and encircle such pairs.
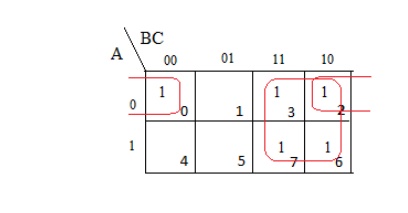
Step 4:
┬Ę Simplify the boolean expression from step 3.
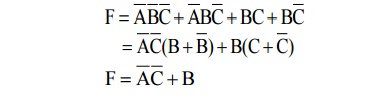
The above boolean expression is simplified by using k-map method.
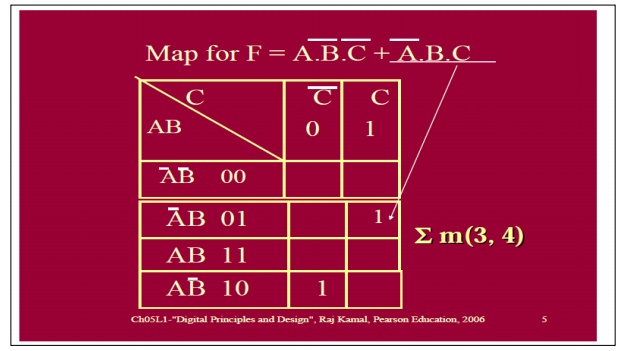
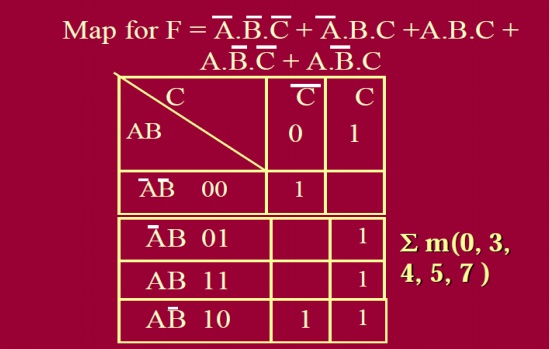
Filling the cell with 1s from SOP form:
1 When output is 1 for a given combination of A, B and C, we place 1 at the corresponding cell.
2 Complete the step 1 for all the rows of truth table with outputs = 1.

CORRESPONDING MAXTERM ╬ĀM(1, 6):
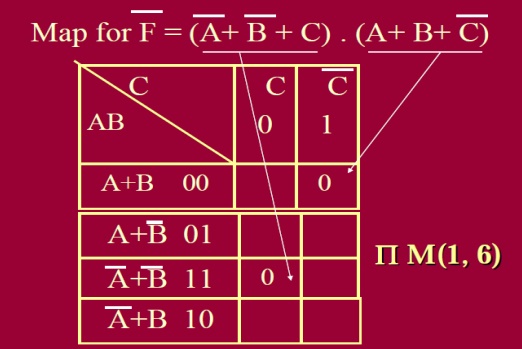
filling the cell with 0s from POS form:
1 When output is 0 for a given combination of A, B and C, we place 0 at the corresponding cell.
2 Complete the step 1 for all 8 rows of truth table with outputs = 0.

2. MAP FROM 4 VARIABLES TRUTH TABLE OR SOP FORM BOOLEAN EXPRESSION:
A two-dimensional map built from a truth table or 4 variables SOP form Boolean Expression. Since number of rows in a four variable (three inputs) truth table are 16, the map has 16 cells _ Four cells horizontal and four cells vertical
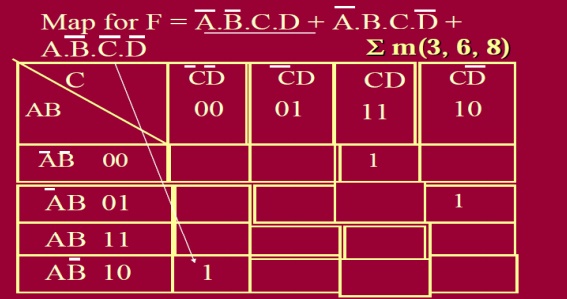
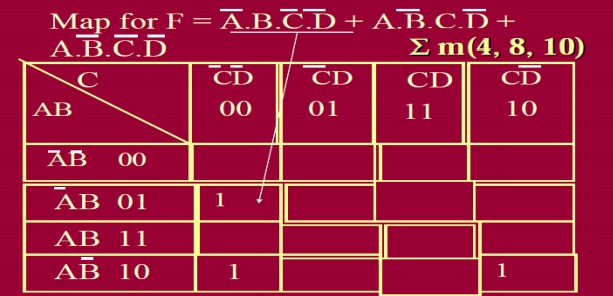
filling the cell with 1s:
1. When output is 1 for a given combination of A, B, C and D, we place 1 at the corresponding cell.
2. Complete the step 1 for all 16 rows of truth table with outputs = 1.

filling the cell with 0s from POS form:
1 When output is 0 for a given combination of A, B and C, we place 0 at the corresponding cell.
2 Complete the step 1 for all the rows of truth table with outputs = 0.


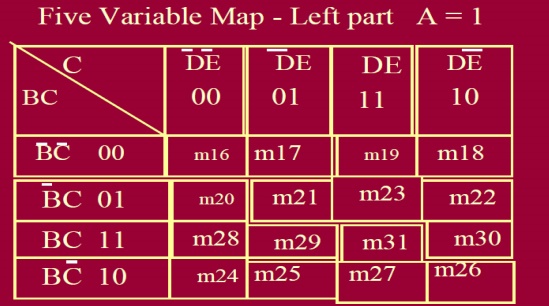
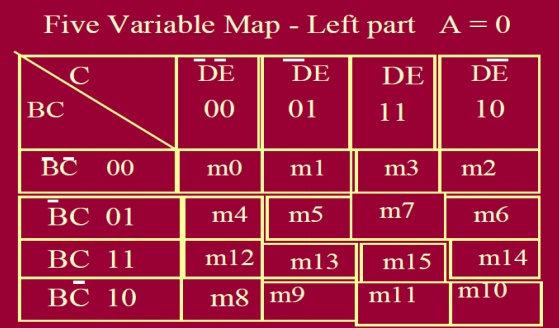
3. FIVE VARIABLE KARNAUGH MAP:
Related Topics