Stratified Random Sampling

Stratified Random Sampling

In Stratified random sampling, the heterogeneous population of size N units is sub-divided into L homogeneous non overlapping sub populations called Strata, the ith  stratum having Ni  units (i =1, 2, 3,…,L) such that N1+N2 +…. +NL = N.

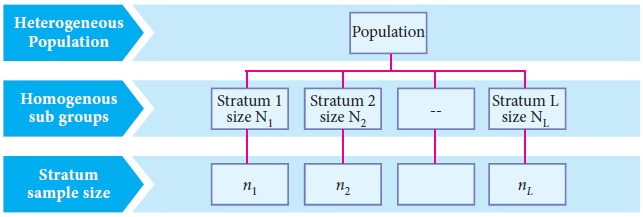
               sample size being ni from ith stratum (i=1, 2,…,L) is independently taken by simple random sampling in such way that n1+n2+… +nL = n. A sample obtained using this procedure is called a stratified random sample.

To determine the sample size for each stratum, there are two methods namely proportionate allocation and optimum allocation. In proportionate allocation sample size is determined as proportionate to stratum size. If the stratum size large, that stratum will get more representation in the sample. If the stratum size small, that stratum will get less representation in the sample. The sample size for the ith stratum can be determined using the formula ni = (n/N)* Ni . The optimum allocation method uses variation in the stratum and cost to determine the stratum sample size ni .

Example 2.2

To study about the introduction of NEET exam, the opinions are collected from 3 schools. The strength of the schools are 2000, 2500 and 4000. It is fixed that the sample size is 170. Calculate the sample size for each school?

Solution

Here N = 2000 + 2500 + 4000 = 8500 and n = 170 then n1 = n2 = n13 = ?

N1 = 2000, N2 = 2500 , N3 = 4000

n1 = (n/N)× N1  = ( 170 / 8500 ) ×2000 = 40

n2 = (n/N)× N2  = ( 170 / 8500 ) × 2500 = 50

n3 = (n/N)× N3  = ( 170 / 8500 ) × 4000 = 80

Therefore 40 students from school 1, 50 students from school 2 and 80 students from school 3, are to be selected using SRS to obtain the required stratified random sample

The main objective of stratification is to give a better cross-section of the population for a higher degree of relative precision. The criteria used for stratification are States, age and sex, academic ability, marital status etc,. In many practical situations when it is difficult to stratify with respect to the characteristic under study, administrative convenience may be considered as the basis for stratification

Merits

·           It provides a chance to study of all the sub-populations separately.

·           An optimum size of the sample can be determined with a given cost, precision and reliability.

·           It is a more precise sample.

·           Representation of sub groups in the population

·           Biases reduced and greater precise.

Limitations

·           There is a possibility of faulty stratification and hence the accuracy may be lost.

·           Proportionate stratification requires accurate information on the proportion of population in each stratum.