Probability sampling

Probability sampling:

Probability sampling or random sampling involves a random selection process to include a unit of the population in the sample. In random sampling, all items have a positive probability of selection. Random sampling techniques remove the personal bias of the investigators. Some of the important methods of probability sampling are: Simple Random Sampling, Stratified Random Sampling and Systematic Sampling.

Simple random sampling

This method selects a sample in such a way that each possible sample to have an equal probability of being selected or each item in the entire population to have an equal probability of being included in the sample. The following are the methods of selecting a simple random sample.

(1) Lottery Method

Suppose that we have to select a random sample of size n from a finite population of size N. First assign numbers 1 to N to all the N units of the population. Then write numbers 1 to N on different identical slips or cards so that a card is not distinguishable from another. They are folded and mixed up in a drum or a box or a container. A blindfold selection is made. The selected card may be replaced or may not be replaced before the next draw. The Required numbers of slips are selected for the desired sample size under any one of these methods forms a simple random sample. The selection of items thus depends on chance.

Simple random sampling without replacement (SRSWOR):

If the selected cards are not replaced before the next draw, such a sampling is called without replacement.

Simple random sampling with replacement (SRSWR):

If the selected cards are replaced before the next draw, such a sampling is called sampling with replacement

Remark: 

 If the population size is large, this method is cumbersome. The alternative method is using of table of random numbers.

(2) Table of Random numbers

The easiest way to select a sample randomly is to use random number tables. There are several tables of random numbers. Some of them are

·           Kendall and Smith random number table.

·           Tippet’s random number table.

·           Fishers and Yates random number table.

Method of using Random Number table.

In a given finite population, the method of selecting a random sample from a random number table is given below:

The table contains different numbers consisting of 0, 1, 2,… ,9 and possesses the essential characteristics which ensures random sampling. A part of the table is given as Appendix. Referring to this page, selection of a random sample is explained by taking a finite population of size 100 units and selecting a sample of 10 units. The steps to be followed are listed as under.

·           A list of all 100 units in the finite population is prepared and each unit is assigned a serial number ranging from 00 to 99.

·           Any number in the table is chosen at random and it is the starting point for selecting the sampling units.

·           From the starting point we can make a move on to the next number either vertically, horizontally or diagonally.

·           Since our numbered population consists of two digits from 00 to 99 , we confine ourselves to reading only two digit numbers without omitting any number that comes forward.

·           As we proceed, random numbers read from the table which are above 99 are ignored and those numbers which are less than are equal to 99 are recorded. This process is continued until we reach 10 such random numbers.

·           If sampling without replacement scheme is followed, a random number once recorded appears again, the same is omitted and we move on to the next number.

·           The 10 such selected random numbers are compared with the labeled (numbered) population units and the corresponding units are selected to get a simple random sample of size 10.

Example 2.1

Select a random sample of size 15 from the random number table from a finite population of size 220.

Step 1 : Assign serial numbers 00 to 219 to the 220 units of the population.

Step 2 : Since the maximum digit is 3, select a three digit as starting point. Let the starting point in the random number table is 066.(first two digits of the entry in the 11^th row and 4^th column).

Step 3 : Continue in the column downwards to select random numbers of size 15.

Step 4 : The numbers chosen to have SRS are 066, 147, 119, 194, 093, 180, 092, 127, 211, 087, 002, 214, 176, 063 and 176. If we get any random number greater than 219, then the multiple of 219 is to be subtracted from the selected number such that the resultant value is less than 219.

Illustration:

Assume that the random is 892. But here, the maximum value assigned for the population is 219 . Hence we select ’4’as the multiplier of 219. Then the random number correspond to 892 is 016. (See: 892 - 4 # 219 = 892 - 876 = 16 )

Case(1) : Under SRSWR: Here the random sample is 066, 147, 119, 194, 093, 180, 092, 127, 211, 087, 002, 214, 176, 063 and 176.

Case(2): Under SRSWOR: Here the random sample is 066, 147, 119, 194, 093, 180, 092, 127, 211, 087, 002, 214, 176, 063and 157.

Merits:

·           It is more representative of the universe.

·           It is free from personal bias and prejudices.

·           The method is simple to use.

·           It is to assess sampling error in the method.

Demerits:

·           If the units are widely dispersed, the sample becomes unrepresentative.

·           The method is not applicable when the units are heterogeneous in nature.

·           Units selected may be too widely dispersed; thus, adherence to the whole sample may be difficult. Remark: Simple random sampling is more suitable when the population is homogeneous. If the population is heterogeneous we must go in for stratified random sampling.

Stratified Random Sampling

In Stratified random sampling, the heterogeneous population of size N units is sub-divided into L homogeneous non overlapping sub populations called Strata, the ith  stratum having N_i  units (i =1, 2, 3,…,L) such that N₁+N₂ +…. +N_L = N.

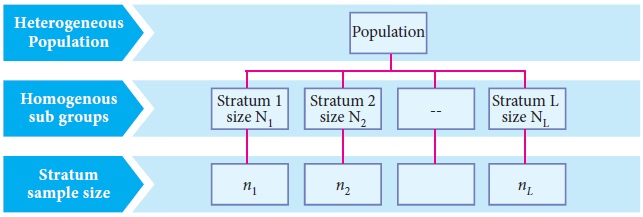
               sample size being n_i from i^th stratum (i=1, 2,…,L) is independently taken by simple random sampling in such way that n₁+n₂+… +n_L = n. A sample obtained using this procedure is called a stratified random sample.

To determine the sample size for each stratum, there are two methods namely proportionate allocation and optimum allocation. In proportionate allocation sample size is determined as proportionate to stratum size. If the stratum size large, that stratum will get more representation in the sample. If the stratum size small, that stratum will get less representation in the sample. The sample size for the ith stratum can be determined using the formula n_i = (n/N)* N_i . The optimum allocation method uses variation in the stratum and cost to determine the stratum sample size ni .

Example 2.2

To study about the introduction of NEET exam, the opinions are collected from 3 schools. The strength of the schools are 2000, 2500 and 4000. It is fixed that the sample size is 170. Calculate the sample size for each school?

Solution

Here N = 2000 + 2500 + 4000 = 8500 and n = 170 then n₁ = n₂ = n₁₃ = ?

N₁ = 2000, N₂ = 2500 , N₃ = 4000

n₁ = (n/N)× N₁  = ( 170 / 8500 ) ×2000 = 40

n₂ = (n/N)× N₂  = ( 170 / 8500 ) × 2500 = 50

n₃ = (n/N)× N₃  = ( 170 / 8500 ) × 4000 = 80

Therefore 40 students from school 1, 50 students from school 2 and 80 students from school 3, are to be selected using SRS to obtain the required stratified random sample

The main objective of stratification is to give a better cross-section of the population for a higher degree of relative precision. The criteria used for stratification are States, age and sex, academic ability, marital status etc,. In many practical situations when it is difficult to stratify with respect to the characteristic under study, administrative convenience may be considered as the basis for stratification

Merits

·           It provides a chance to study of all the sub-populations separately.

·           An optimum size of the sample can be determined with a given cost, precision and reliability.

·           It is a more precise sample.

·           Representation of sub groups in the population

·           Biases reduced and greater precise.

Limitations

·           There is a possibility of faulty stratification and hence the accuracy may be lost.

·           Proportionate stratification requires accurate information on the proportion of population in each stratum.

Systematic Sampling

In systematic sampling, the population units are numbered from 1 to N in ascending order. A sampling interval, denoted by k, is determined as k=N/n, where n denotes the required sample size. Then n–1 such sampling intervals each consisting of k units will be formed. A number is selected at random from the first sampling interval. Let it be number i where i ≤ k. This number is the random starting point for the whole selection of the sample. The unit corresponding to i is the first unit in the sample. The subsequent sampling units are the units in the following positions:

i, k +i, 2k +i, 3k + i , …, nk

Thus, with selection of the first unit, the whole sample is selected automatically. As the first unit could have been any of the k units, the technique will generate k systematic samples with equal probability. If N is not an integral multiple of n, then sizes of a few possible systematic samples may vary by one unit.

Merits:

·           This method is simple and convenient.

·           Less time consuming.

·           It can be used in infinite population.

Limitation:

·           Since it is a quasi random sampling, the sample may not be a representative sample.

Example 2.3

Suppose a systematic random sample of size n = 10 is needed from a population of size N = 200, the sampling interval k=N/n=200/10=20.

The first sampling interval consists of numbers 1 to 20. If the randomly selected number (random starter) is 7, the systematic sample will consist units corresponding to positions 7, 27,47,67,87,107,127,14 7,167,187.

Applications:

·           Systematic sampling is preferably used when the information is to be collected from trees in a highway, houses in blocks, etc,.

·           This method is often used in industry, where an item is selected for testing from a production line (say, every fifteenth item in the order of production) to ensure that equipments are working satisfactorily.

·           This technique could also be used in a sample survey for interviewing people. A market researcher might select every 10th person who enters a particular store, after selecting a person at random as a random start.