Chapter: Introduction to the Design and Analysis of Algorithms : Divide and Conquer
StrassenŌĆÖs Matrix Multiplication
Multiplication of Large Integers and StrassenŌĆÖs Matrix Multiplication
In this section, we examine two surprising algorithms for seemingly straightfor-ward tasks: multiplying two integers and multiplying two square matrices. Both achieve a better asymptotic efficiency by ingenious application of the divide-and-conquer technique.
StrassenŌĆÖs
Matrix Multiplication
Now that
we have seen that the divide-and-conquer approach can reduce the number of
one-digit multiplications in multiplying two integers, we should not be
surprised that a similar feat can be accomplished for multiplying matrices.
Such an algorithm was published by V. Strassen in 1969 [Str69]. The principal
insight of the algorithm lies in the discovery that we can find the product C of two 2 ├Ś 2 matrices A and B with
just seven multiplications as opposed to the eight required by the brute-force
algorithm (see Example 3 in Section 2.3). This is accomplished by using the
following formulas:
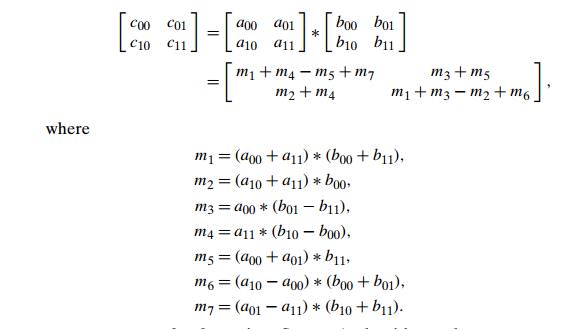
Thus, to
multiply two 2 ├Ś 2
matrices, StrassenŌĆÖs algorithm makes seven multipli-cations and 18
additions/subtractions, whereas the brute-force algorithm requires eight
multiplications and four additions. These numbers should not lead us to
multiplying 2 ├Ś 2
matrices by StrassenŌĆÖs algorithm. Its importance stems from its asymptotic superiority as matrix order n goes to infinity.
Let A and B be two n ├Ś n matrices where n is a power of 2. (If n is not a power of 2, matrices
can be padded with rows and columns of zeros.) We can divide A, B,
and their
product C into four n/2
├Ś n/2 submatrices each as follows:
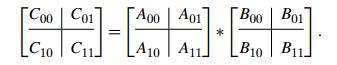
It is not
difficult to verify that one can treat these submatrices as numbers to get the
correct product. For example, C00 can be
computed either as A00 ŌłŚ B00 +
A01 ŌłŚ B10 or as
M1 + M4 ŌłÆ M5 + M7 where
M1, M4, M5, and
M7 are found
by StrassenŌĆÖs formulas, with the
numbers replaced by the corresponding submatrices.
If the
seven products of n/2 ├Ś n/2
matrices are computed recursively by the same method, we have StrassenŌĆÖs
algorithm for matrix multiplication.
Let us
evaluate the asymptotic efficiency of this algorithm. If M(n) is the number of multiplications
made by StrassenŌĆÖs algorithm in multiplying two n ├Ś n matrices
(where n is a power of 2), we get the
following recurrence relation for it:
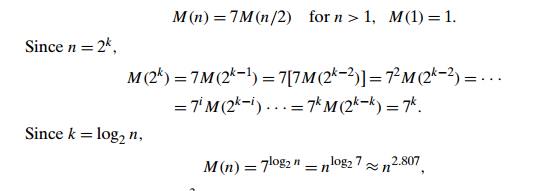
which is
smaller than n3 required
by the brute-force algorithm.
Since
this savings in the number of multiplications was achieved at the expense of
making extra additions, we must check the number of additions A(n) made by StrassenŌĆÖs algorithm. To
multiply two matrices of order n > 1, the
algorithm needs to multiply seven matrices of order n/2 and
make 18 additions/subtractions of matrices of size n/2; when n = 1, no additions are made since two
numbers are
simply
multiplied. These observations yield the following recurrence relation:
A(n) = 7A(n/2)
+ 18(n/2)2 for n
> 1, A(1)
= 0.
Though
one can obtain a closed-form solution to this recurrence (see Problem 8 in this
sectionŌĆÖs exercises), here we simply establish the solutionŌĆÖs order of growth.
According to the Master Theorem, A(n) Ōłł (nlog 2
7). In other words, the number of
additions has the same order of growth as the number of multiplications. This
puts StrassenŌĆÖs algorithm in (nlog2 7), which is a better efficiency
class than (n3) of the brute-force method.
Since the
time of StrassenŌĆÖs discovery, several other algorithms for multiplying two n ├Ś n matrices of real numbers in O(n╬▒) time
with progressively smaller constants ╬▒ have
been invented. The fastest algorithm so far is that of Coopersmith and Winograd
[Coo87] with its efficiency in O(n2.376). The decreasing values of the
exponents have been obtained at the expense of the increasing complexity of
these algorithms. Because of large multiplicative constants, none of them is of
practical value. However, they are interesting from a theoretical point of
view. On one hand, they get closer and closer to the best theoretical lower
bound known for matrix multiplication, which is n2
multiplications, though the gap between this bound and the best available
algorithm remains unresolved. On the other hand, matrix multiplication is known
to be computationally equivalent to some other important problems, such as
solving systems of linear equations (discussed in the next chapter).
Exercises
5.4
What are the smallest and largest numbers of digits
the product of two decimal n-digit
integers can have?
Compute 2101 ŌłŚ 1130 by
applying the divide-and-conquer algorithm outlined in the text.
a. Prove the equality alogb c = clogb a, which was used in Section 5.4.
Why is nlog2 3
better than 3log2 n as a
closed-form formula for M(n)?
a. Why did
we not include multiplications by 10n in the multiplication count M(n)
of the
large-integer multiplication algorithm?
In addition to assuming that n is a power of 2, we made, for
the sake of simplicity, another, more subtle, assumption in setting up the
recurrences for M(n) and A(n), which is not always true (it
does not change the final answers, however). What is this assumption?
How many one-digit additions are made by the
pen-and-pencil algorithm in multiplying two n-digit
integers? You may disregard potential carries.
Verify
the formulas underlying StrassenŌĆÖs algorithm for multiplying 2 ├Ś 2 matrices.
7. Apply StrassenŌĆÖs algorithm to
compute
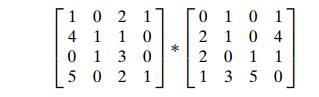
exiting the recursion when n = 2, i.e., computing the products of
2 ├Ś 2 matrices by the brute-force
algorithm.
Solve the recurrence for the number of additions
required by StrassenŌĆÖs algo-rithm. Assume that n is a
power of 2.
V. Pan [Pan78] has discovered a divide-and-conquer
matrix multiplication algorithm that is based on multiplying two 70 ├Ś 70 matrices using 143,640
multiplications. Find the asymptotic efficiency of PanŌĆÖs algorithm (you may
ignore additions) and compare it with that of StrassenŌĆÖs algorithm.
Practical implementations of StrassenŌĆÖs algorithm
usually switch to the brute-force method after matrix sizes become smaller than
some crossover point. Run an experiment to determine such a crossover point on
your computer system.
Related Topics