Static and Dynamic Response

STATIC AND DYNAMIC RESPONSE

The static characteristics of measuring instruments are concerned only with the steady-state reading that the instrument settles down to, such as accuracy of the reading.

The dynamic characteristics of a measuring instrument describe its behavior between the time a measured quantity changes value and the time when the instrument output attains a steady value in response. As with static characteristics, any values for dynamic characteristics quoted in instrument data sheets only apply when the instrument is used under specified environmental conditions. Outside these calibration conditions, some variation in the dynamic parameters can be expected.

In any linear, time-invariant measuring system, the following general relation can be written between input and output for time (t) > 0:

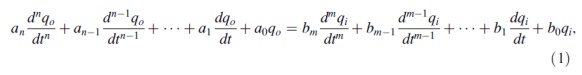
where q_i is the measured quantity, qo is the output reading, and a_o ...a_n, b_o... b_m are constants. If we limit consideration to that of step changes in the measured quantity only, then Equation (2) reduces to

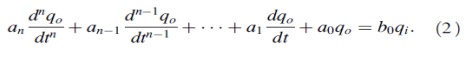
Zero-Order Instrument

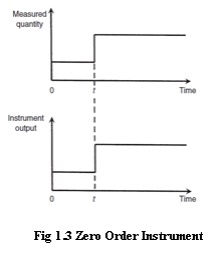
If all the coefficients a1 . . . an other than a0  in Equation (2) are assumed zero, then where K is a constant known as the instrument sensitivity as defined earlier. Any instrument that behaves according to Equation (3) is said to be of a zero-order type. Following a step change in the measured quantity at time t, the instrument output moves immediately to a new value at the same time instant t, as shown in Figure. A potentiometer,  which measures motion is a good example of such an instrument, where the output voltage changes instantaneously as the slider is displaced along the potentiometer track.

First-Order Instrument

If all the coefficients a2 . . . an except for ao and a1 are assumed zero in Equation (2) then

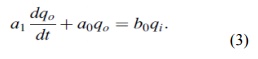
Any instrument that behaves according to Equation (4) is known as a first-order instrument. If d/dt is replaced by the D operator in Equation (4), we get

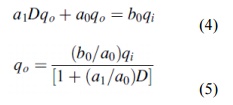
Defining K ¼ b₀/a₀ as the static sensitivity and t ¼ a₁/a₀ as the time constant of the system,

Equation (5) becomes

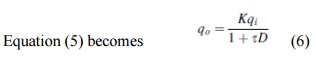
Second-Order Instrument

If all coefficients a₃ . . . other than a₀, a₁, and a₂ in Equation (2) are assumed zero, then we get

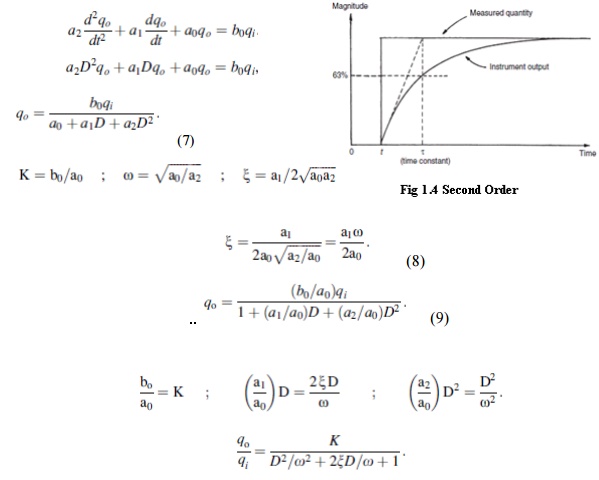
This is the standard equation for a second-order system, and any instrument whose response can be described by it is known as a second-order instrument. If Equation (9) is solved analytically, the shape of the step response obtained depends on the value of the damping ratio parameter x. The output responses of a second-order instrument for various values of x following a step changein the value of the measured quantity at time t are shown in Figure. Commercial second-order instruments, of which the accelerometer is a common example, are generally designed to have a damping ratio (x) somewhere in the range of 0.6–0.8.