Solved Example Problems: Area of a Triangle and Quadrilateral

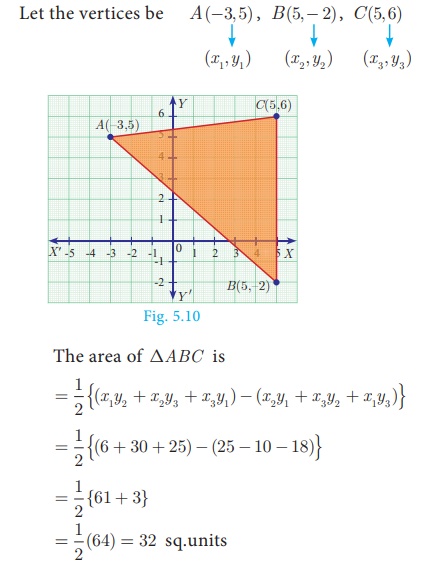
Example 5.1

Find the area of the triangle whose vertices are (-3, 5) , (5, 6) and (5, - 2)

Solution

Plot the points in a rough diagram and take them in  counter-clockwise order.

Example 5.2

Show that the points P(-1.5, 3) , Q(6 , -2) , R(-3 , 4) are collinear.

Solution

The points are P(-1. 5, 3) , Q(6 , -2) , R(-3 , 4)

Area of ΔPQR = 1/2{(x ₁y₂  + x ₂y₃  + x ₃y₁ ) −(x ₂y₁ + x ₃y₂  + x ₁y₃ )}

=1/2 {(3 + 24 − 9) −(18 + 6 − 6)} = 1/2{18 −18} = 0

Therefore, the given points are collinear.

Example 5.3

If the area of the triangle formed by the vertices A(-1, 2) , B (k , -2) and C(7, 4) (taken in order) is 22 sq. units, find the value of k.

Solution

The vertices are A(-1, 2) , B (k , -2) and C(7, 4)

Area of triangle ABC is 22 sq.units

2k + 34 = 44 gives 2k = 10 so k = 5

Example 5.4

If the points P(- 1, -4) , Q (b,c) and R(5, -1) are collinear and if 2b + c = 4 , then find the values of b and c.

 Solution

Since the three points P(- 1, - 4) , Q (b,c) and R(5, -1) are collinear,

 Area of triangle PQR = 0

−c −b − 20 + 4b − 5c −1  = 0

b - 2c = 7        …(1)

Also, 2b + c = 4      …(2) (from given information)

Solving (1) and (2) we get b = 3 , c = −2

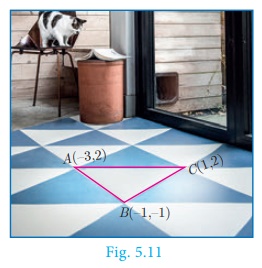
Example 5.5

The floor of a hall is covered with identical tiles which are in the shapes of triangles. One such triangle has the vertices at (-3 , 2) , (- 1 , -1) and (1 , 2) . If the floor of the hall is completely covered by 110 tiles, find the area of the floor.

Solution

Vertices of one triangular tile are at 

(-3 , 2) , (- 1 , -1) and (1 , 2)

Area of this tile  = 1/2 {(3 − 2 + 2) −(− 2 −1 − 6)} sq.units

= 1/2(12) = 6 sq.units

Since the floor is covered by 110 triangle shaped identical tiles,

Area of floor = 110 ×6 = 660 sq.units

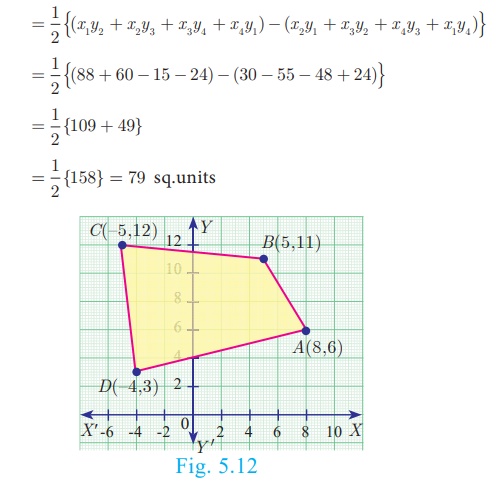
Example 5.6

Find the area of the quadrilateral formed by the points (8, 6) , (5, 11) , (-5, 12) and (-4, 3) .

Solution

Before determining the area of quadrilateral, plot the vertices in a graph. Let the vertices be A(8,6), B(5,11), C(–5,12) and D(–4,3)

Therefore, area of the quadrilateral ABCD

Example 5.7

The given diagram shows a plan for constructing a new parking lot at a campus. It is estimated that such construction would cost ₹1300 per square feet. What will be the total cost for making the parking lot?

Solution

The parking lot is a quadrilateral whose vertices are  at A(2, 2) , B(5, 5) , C(4, 9) and D(1, 7) .

Therefore, Area of parking lot

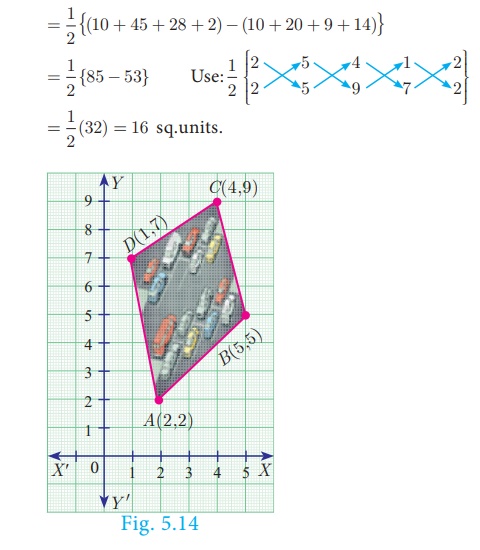
So, area of parking lot = 16 sq.feets

Construction rate per square feet = ₹1300

Therefore, total cost for constructing the parking lot = 16 ×1300 = ₹20800