Exercise 5.4: General Form of a Straight Line

Exercise 5.4

1. Find the slope of the following straight lines

(i) 5y − 3 = 0   (ii) 7x – 3/17 = 0

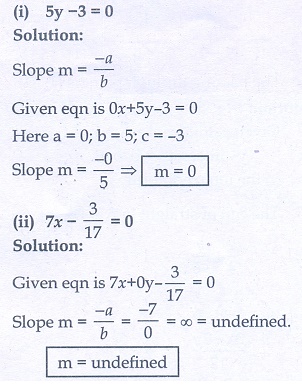
2. Find the slope of the line which is

(i) parallel to y = 0. 7x −11

(ii) perpendicular to the line x = −11

3. Check whether the given lines are parellel or perpendicular

(i) x/3 + y/4 + 1/7 = 0 and 2x/3 + y/2 + 1/10 = 0

(ii) 5x + 23y + 14 = 0 and 23x − 5y + 9 = 0

4. If the straight lines 12y = −( p + 3)x + 12 , 12x − 7y = 16 are perpendicular then find ‘p’.

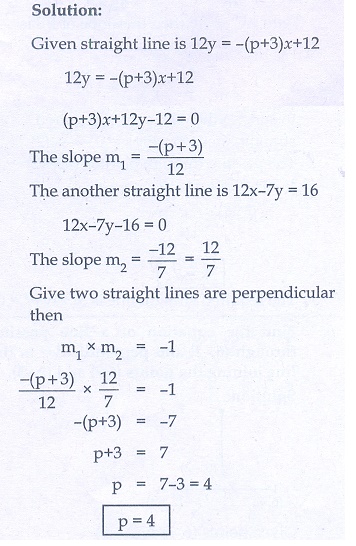
5. Find the equation of a straight line passing through the point P(-5, 2) and parallel to the line joining the points Q(3, - 2) and R(-5, 4)

6. Find the equation of a line passing through (6,–2) and perpendicular to the line joining the points (6,7) and (2,–3).

7. A(-3, 0) B(10, - 2) and C(12, 3) are the vertices of ΔABC . Find the equation of the altitude through A and B.

8. Find the equation of the perpendicular bisector of the line joining  the points A(-4, 2) and B(6, - 4) .

9. Find the equation of a straight line through the intersection of lines 7x + 3y = 10 , 5x − 4y = 1 and parallel to the line 13x + 5y + 12 = 0

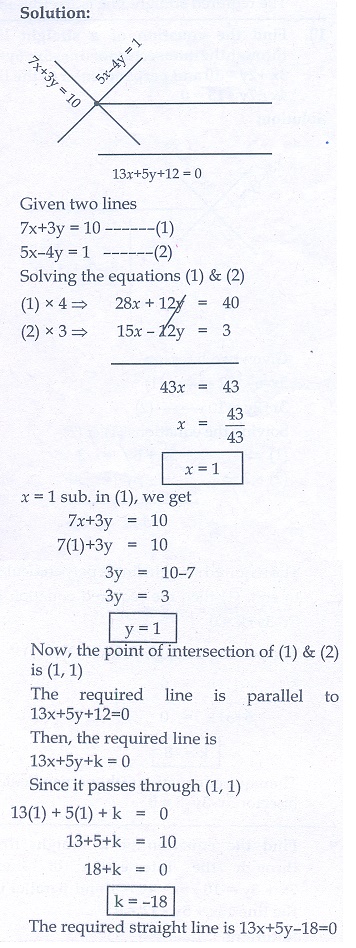
10. Find the equation of a straight line through the intersection of lines 5x − 6y = 2 , 3x + 2y = 10 and perpendicular to the line 4x − 7y + 13 = 0

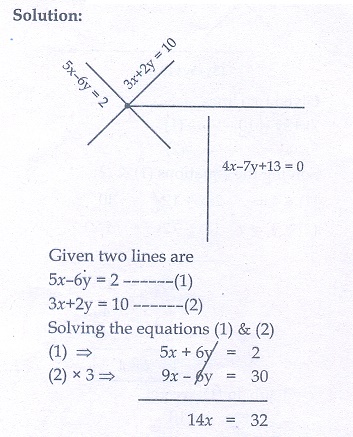
11. Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x − 2y − 4 = 0 to the point of intersection of 7x − 3y = −12 and 2y = x + 3

12. Find the equation of a straight line through the point of intersection of the lines 8x + 3y = 18 , 4x + 5y = 9 and bisecting the line segment joining the points (5,–4) and (–7,6).

Answers:

1.(i) 0 (ii) undefined

2.(i) 0.7 (ii) undefined

3.(i) Parallel (ii) Perpendicular

4. 4

5. 3x + 4y + 7 = 0

6. 2x + 5y − 2 = 0

7. 2x + 5y + 6 = 0 , 5x + y − 48 = 0

8. 5x − 3y − 8 = 0

9. 13x + 5y − 18 = 0

10. 49x + 28y −156 = 0

11. 31x + 15y + 30 = 0

12. 4x + 13y − 9 = 0