Inclination of a line

Inclination of a line

The inclination of a line or the angle of inclination of a line is the angle which a straight line makes with the positive direction of X axis measured in the counter-clockwise direction to the part of the line above the X axis. The inclination of the line is usually denoted by θ.

Note

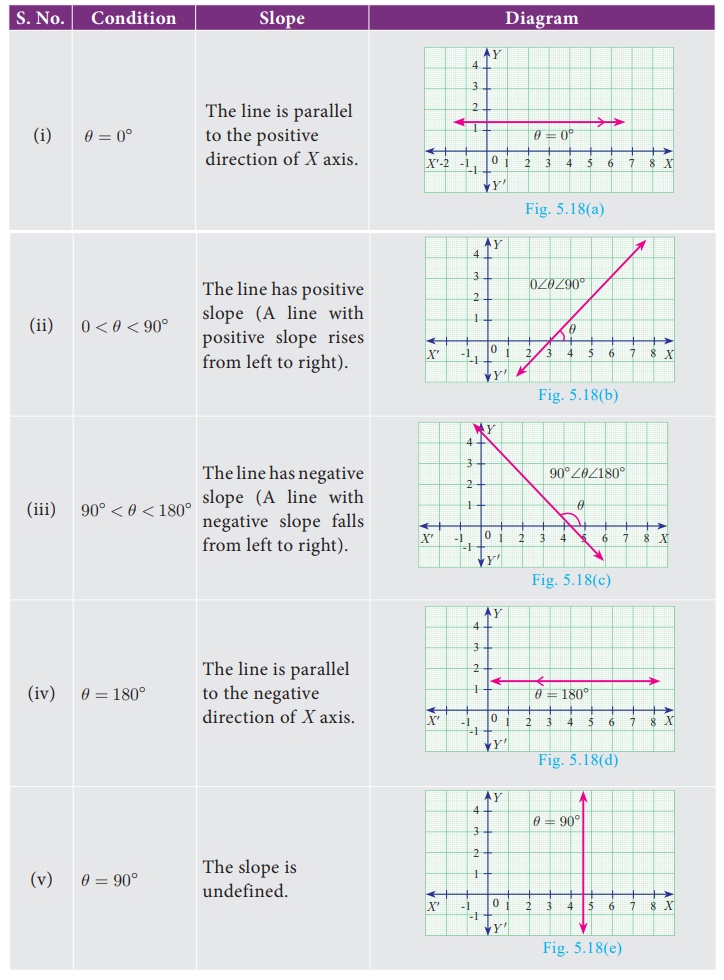
·           The inclination of X axis and every line parallel to X axis is 0°.

·           The inclination of Y axis and every line parallel to Y axis is 90°.

1. Slope of a Straight line

While laying roads one must know how steep the road will be. Similarly, when constructing a staircase, we should consider its steepness. For the same reason, anyone travelling along a hill or a bridge, feels hard compared to travelling along a plain road.

All these examples illustrate one important aspect called “Steepness”. The measure of steepness is called slope or gradient.

The concept of slope is important in economics because it is used to measure the rate at which the demand for a product changes in a given period of time on the basis of its price. Slope comprises of two factors namely steepness and direction.

Definition

If θ is the angle of inclination of a non -vertical straight line, then tanθ is called the slope or gradient of the line and is denoted by m.

Therefore the slope of the straight line is m = tan θ , 0 ≤ θ ≤ 180° , θ ≠ 90°

To find the slope of a straight line when two points are given

Slope m = tan θ

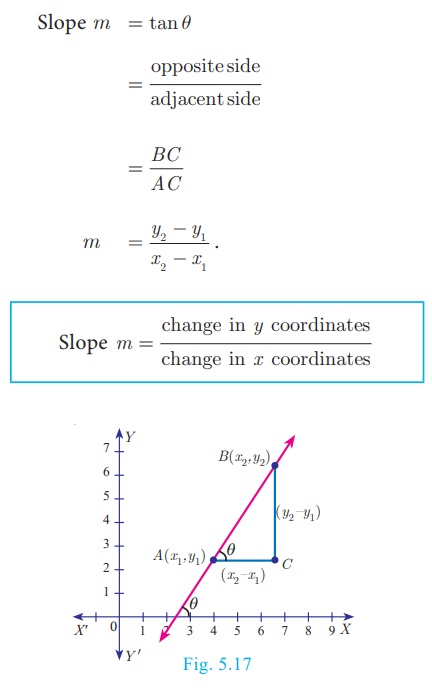
The slope of the line through (x ₁ , y₁ ) and (x ₂ , y₂ ) with x ₁ ≠ x₂ is .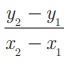

Note

The slope of a vertical line is undefined

Values of slopes

2. Slopes of parallel lines

Two non-vertical lines are parallel if and only if their slopes are equal.

Let l₁ and l₂ be two non-vertical lines with slopes m₁ and m₂ respectively.

Let the inclination of the lines with positive direction of X axis be θ₁ and θ₂ respectively.

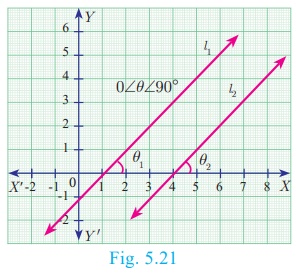
Assume, l₁ and l₂are parallel

θ₁ = θ₂   (Since, θ₁ , θ₂  are corresponding angles)

tan θ₁= tan θ₂

m₁= m₂

Hence, the slopes are equal.

Therefore, non-vertical parallel lines have equal slopes.

Conversely

Let the slopes be equal, then m₁ = m₂

tan θ ₁= tan θ ₂

θ₁= θ₂ (since 0 ≤ θ₁ , θ₂  ≤ 180°)

That is the corresponding angles are equal.

Therfore, l₁  and l₂ are parallel

Thus, non-vertical lines having equal slopes are parallel.

Hence, non vertical lines are parallel if and only if their slopes are equal.

3. Slopes of perpendicular lines

Two non-vertical lines with slopes m₁ and m₂ are perpendicular if and only if m₁m₂ = −1

Let l₁ and l₂ be two non-vertical lines with slopes m₁ and m₂ , respectively. Let their inclinations be θ₁ and θ₂ respectively.

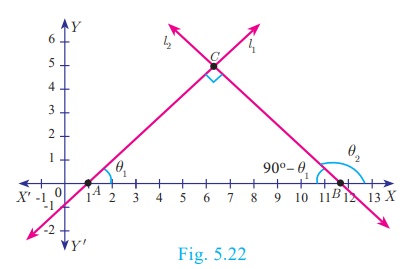
Then m₁  = tan θ₁  and m₂  = tan θ₂

First we assume that, l₁ and l₂ are perpendicular to each other. 

Then ∠ABC = 90° − θ₁  (sum of angles of ΔABC is 180° )

Now measuring slope of l₂ through angles θ₂ and 90° − θ₁ , which are opposite to each other, we get

tan θ₂ = −tan(90° − θ₁ )

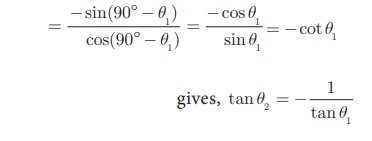
tan θ₁ . tan θ₂ = −1

m₁ .m₂ = −1

Thus, when the line l₁ is perpendicular to line l₂  then m₁m₂  = −1 .

Conversely,

Let l₁ and l₂ be two non-vertical lines with slopes m₁ and m₂ respectively, such that m₁m₂ = −1 .

Since m₁ = tan θ ₁ , m₂ = tan θ₂

We have tan θ₁ tan θ₂ = −1

tan θ₁ = −1/ tan θ₂

tan θ₁ = −cot θ₂

tan θ₁ = −tan(90° - θ₂)

tan θ₁ = tan(-(90° - θ₂)) = tan(θ₂ - 90°)

θ₁ = θ₂ - 90°         (since 0 ≤ θ_1, θ₂ ≤ 180)

θ₂ = 90° + θ₁

But in ΔABC, θ₂ = ∠C + θ₁

Therefore, ∠C = 90°

Note 

Let l₁ and l₂ be two lines with well-defined slopes m₁  and m₂  respectively, then

(i) l₁ is parallel to l₂ if and only if m₁ = m₂ .

(ii) l₁ is perpendicular to l₂ if and only if m₁m₂ = −1.

Example 5.8

(i) What is the slope of a line whose inclination is 30° ?

(ii) What is the inclination of a line whose slope is √3?

Solution

(i) Here θ = 30°

Slope m = tan θ

Therefore, slope m = tan 30° = 1 /√3

(ii) Given m = √3 let θ be the inclination of the line

tan θ =  √3

We get, θ = 60°

Example 5.9

Find the slope of a line joining the given points

 (i) (-6, 1) and (-3, 2) (ii) (-1/3, ½) , and (2/7, 3/7) (iii) (14, 10) and (14, -6)

Solution

(i) (-6, 1) and (-3, 2)

The slope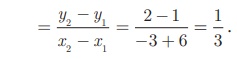 

(iii) (14, 10) and (14, - 6) 

The slope is undefined.

Example 5.10

The line r passes through the points (–2, 2) and (5, 8) and the line s passes through the points (–8, 7) and (–2, 0). Is the line r perpendicular to s ?

Solution

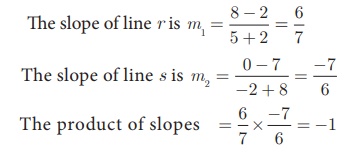
That is,m₁m₂ = −1

Therefore, the line r is perpendicular to line s.

Example 5.11

The line p passes through the points (3, - 2) , (12, 4) and the line q passes through the points (6, - 2) and (12, 2) . Is p parallel to q ?

Solution

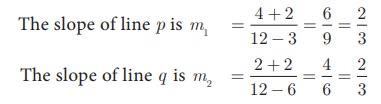
Thus, slope of line p = slope of line q.

Therefore, line p is parallel to the line q.

Example 5.12

Show that the points (-2, 5) , (6, -1) and (2, 2) are collinear.

Solution 

The vertices are A(-2, 5) , B(6, -1) and C(2, 2).

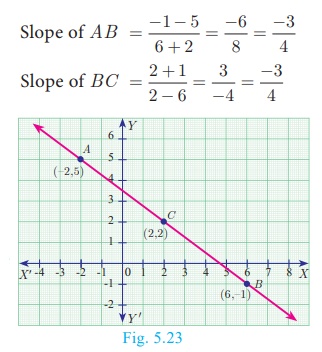
We get, Slope of AB = Slope of BC

Therefore, the points A, B, C all lie in a same straight line.

Hence the points A, B and C are collinear.

Example 5.13

Let A(1, - 2) , B(6, - 2) , C(5, 1) and D(2, 1) be four points

(i) Find the slope of the line segments (a) AB (b) CD

(ii) Find the slope of the line segments (a) BC (b) AD

(iii) What can you deduce from your answer.

Solution

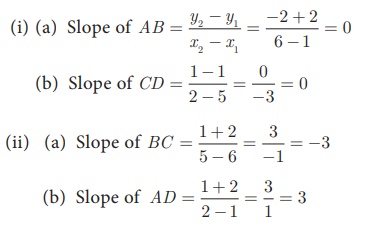
(iii) The slope of AB and CD are equal so AB, CD are parallel.

Similarly the lines AD and BC are not parallel, since their slopes are not equal. So, we can deduce that the quadrilateral ABCD is a trapezium.

Example 5.14

Consider the graph representing growth of population (in crores). Find the slope of the line AB and hence estimate the population in the year 2030? 

Solution

The points A(2005, 96) and B(2015, 100) are on the line AB.

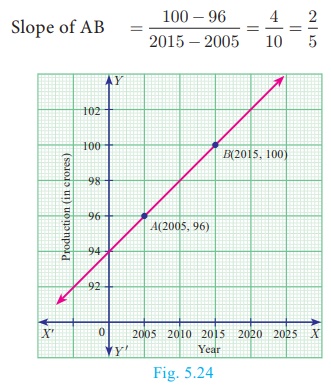
Let the growth of population in 2030 be k crores.

Assuming that the point C (2030,k) is on AB, 

we have, slope of AC = slope of AB

k - 96 = 10

k = 106

Hence the estimated population in 2030 = 106 Crores.

Example 5.15

Without using Pythagoras theorem, show that the points (1, - 4) , (2, - 3) and (4, - 7) form a right angled triangle.

Solution

Let the given points be A(1, - 4) , B(2, - 3) and C(4, - 7).

Slope of AB × slope of AC = (1)(−1) = −1

AB is perpendicular to AC. ∠A = 90°

Therefore, ΔABC is a right angled triangle.

Example 5.16

Prove analytically that the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is equal to half of its length.

Solution

Let P (a,b) Q (c,d) and R(e, f ) be the vertices of a triangle.

Let S be the mid-point of PQ and T be the mid-point of PR

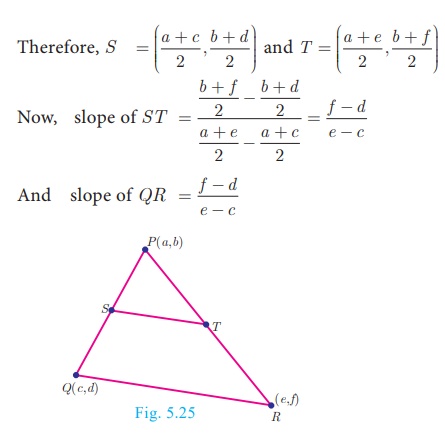
Therefore, ST is parallel to QR. (since, their slopes are equal)

Also   

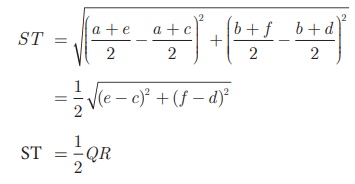
Thus ST is parallel to QR and half of it.

Note

This example illustrates how a geometrical result can be proved using coordinate Geometry.