General Form of a Straight Line

General Form of a Straight Line

The linear equation (first degree polynomial in two variables x and y) ax + by +c = 0 (where a, b and c are real numbers such that at least one of a, b is non-zero) always represents a straight line. This is the general form of a straight line.

Now, let us find out the equations of a straight line in the following cases

(i) parallel to ax + by + c = 0

(ii) perpendicular to  ax + by + c = 0

(iii) The point of intersection of two intersecting straight lines

1. Equation of a line parallel to the line ax + by +c = 0

The equation of all lines parallel to the line ax + by +c = 0 can be put in the form ax + by + k = 0 for different values of k

2. Equation of a line perpendicular to the line ax + by +c = 0

The equation of all lines perpendicular to the line ax + by +c = 0 can be written as bx − ay + k = 0 for different values of k.

3. Slope of a straight line

The general form of the equation of a straight line is ax + by +c = 0 . (at least one of a, b is non-zero)

coefficient of x = a , coefficient of y = b , constant term = c.

The above equation can be rewritten as by = −ax –c

Gives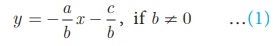  

comparing (1) with the form y = mx +l

We get, slope m = − a/b

m = −coefficient of x / coefficient of y

y intercept l = − c/b

y intercept = −constant term / coefficient of y

Example 5.30

Find the slope of the straight line 6x + 8y + 7 = 0 .

Solution

Given 6x + 8y + 7 = 0

 slope m = 

Therefore, the slope of the straight line is – 3/4.

Example 5.31

Find the slope of the line which is 

(i) parallel to 3x − 7y = 11

(ii) perpendicular to 2x − 3y + 8 = 0

Solution

(i) Given straight line is 3x − 7y = 11

gives 3x - 7y –11  = 0

Slope m= − 3/-7 = 3/7

Since parallel lines have same slopes, slope of any line parallel to

 3x − 7y = 11  is  3/7

(ii) Given straight line is 2x − 3y + 8 = 0

Slope m = −2/−3  = 23

Since product of slopes is −1 for perpendicular lines, slope of any line perpendicular to 2x − 3y + 8 = 0 is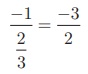 

Example 5.32

Show that the straight lines 2x + 3y − 8 = 0  and  4x + 6y + 18 = 0 are parallel.

Solution

Slope of the straight line 2x + 3y − 8 = 0 is

m₁ = − coefficient of x / coefficient of y

m₁ = − 2/3

Slope of the straight line 4x + 6y + 18 = 0 is

m₂ = −4/6 = −2/3

Here, m₁   = m₂

That is, slopes are equal. Hence, the two straight lines are parallel.

Example 5.33

Show that the straight lines x − 2y + 3 = 0 and 6x + 3y + 8 = 0 are perpendicular.

Solution

Slope of the straight line x − 2y + 3 = 0 is

m₁ = −1/−2 = 1/2

Slope of the straight line 6x + 3y + 8 = 0 is

m₂ = −6/3 = −2

 Now, m₁ × m₂  = 1/2 × (−2) = −1

Hence, the two straight lines are perpendicular.

Example 5.34

Find the equation of a straight line which is parallel to the line 3x − 7y = 12 and passing through the point (6,4).

Solution

Equation of the straight line, parallel to 3x − 7y −12 = 0 is 3x − 7y + k = 0 Since it passes through the point (6,4)

3(6) − 7(4) + k= 0

k = 28 −18 = 10

Therefore, equation of the required straight line is 3x − 7y + 10 = 0.

Example 5.35

Find the equation of a straight line perpendicular to the line 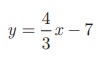  and passing through the point (7, –1).

Solution

The equation 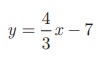 can be written as 4x − 3y − 21 = 0 .

Equation of a straight line perpendicular to 4x − 3y − 21 = 0 is 3x + 4y + k = 0

Since it is passes through the point (7, –1),

21 − 4 + k = 0 we get, k = −17

Therefore, equation of the required straight line is 3x + 4y −17 = 0 .

Example 5.36

Find the equation of a straight line parallel to Y axis and passing through the point of intersection of the lines 4x + 5y = 13 and x − 8y + 9 = 0 .

Solution

Given lines 4x + 5y −13= 0   ...(1)

x − 8y + 9 = 0                        ...(2) 

To find the point of intersection, solve equation (1) and (2)

The equation of the line is x = 59/37 gives 37x − 59 = 0

Example 5.37

The line joining the points A(0, 5) and B(4, 1) is a tangent to a circle whose centre C is at the point (4, 4) find

(i) the equation of the line AB.

(ii) the equation of the line through C which is perpendicular to the line AB.

(iii) the coordinates of the point of contact of tangent line AB with the circle.

Solution

(i) Equation of line AB, A(0, 5) and B(4, 1)

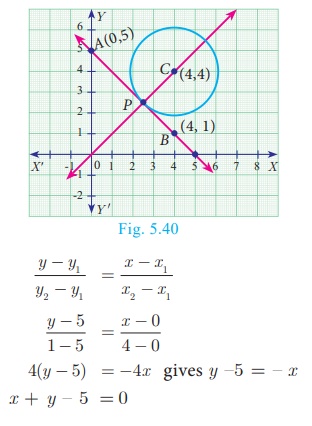
(ii) The equation of a line which is perpendicular to the line AB : x + y − 5 = 0 is x − y + k = 0 

Since it is passing through the point (4,4), we have 4 – 4 + k = 0 gives k = 0

The equation of a line which is perpendicular to AB and through C is x − y = 0...(2)

(iii) The coordinate of the point of contact P of the tangent line AB with the circle is point of intersection of lines.

x + y − 5 = 0  and x − y = 0

solving, we get x = 5/2 and y = 5/2

Therefore, the coordinate of the point of contact is P(5/2,5/2).