Linear programming problem - Solution of LPP by graphical method | 11th Business Mathematics and Statistics(EMS) : Chapter 10 : Operations Research
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 10 : Operations Research
Solution of LPP by graphical method
Solution of LPP by
graphical method
After formulating the linear
programming problem, our aim is to determine the values of decision variables
to find the optimum (maximum or minimum) value of the objective function.
Linear programming problems which involve only two variables can be solved by
graphical method. If the problem has three or more variables, the graphical
method is impractical.
The major steps involved in this
method are as follows
(i) State
the problem mathematically
(ii) Write
all the constraints in the form of equations and draw the graph
(iii) Find
the feasible region
(iv) Find
the coordinates of each vertex (corner points) of the feasible region. The
coordinates of the vertex can be obtained either by inspection or by solving
the two equations of the lines intersecting at the point
(v) By
substituting these corner points in the objective function we can get the
values of the objective function
(vi) If
the problem is maximization then the maximum of the above values is the optimum
value. If the problem is minimization then the minimum of the above values is
the optimum value
Example 10.5
Solve the following LPP
Maximize Z = 2 x1 +5x2
subject to the conditions x1+ 4x2 ≤ 24
3x1+x2
≤ 21
x1+x2 ≤ 9and x1, x2 ≥ 0
Solution:
First we
have to find the feasible region using the given conditions.
Since
both the decision variables x1
and x2 are non-negative
,the solution lies in the first quadrant.
Write all the inequalities of the
constraints in the form of equations.
Therefore we have the lines x1+ 4x2=24 ; 3x1
+ x2 = 21; x1 + x2= 9 x1+
4x2= 24 is a line passing
through the points (0 , 6) and (24 , 0). [(0,6) is obtained by taking x1=0 in x1 + 4x2
= 24 , (24 , 0) is obtained by taking x2
= 0 in x1+ 4x2 = 24].
Any point lying on or below the
line x1 + 4x2 = 24 satisfies the
constraint x1 + 4x2≤
24 .
3x1 +x2= 21 is a line passing through the points (0, 21) and
(7, 0). Any point lying on or below
the line 3 x1 + x2 = 21 satisfies the
constraint 3 x1 + x2 ≤ 21.
x1+ x2 = 9 is a line passing through the points (0 , 9) and ( 9 , 0) .Any
point lying on or below the line x1 + x2 = 9 satisfies the constraint x1+ x2
≤ 9.
Now we
draw the graph.
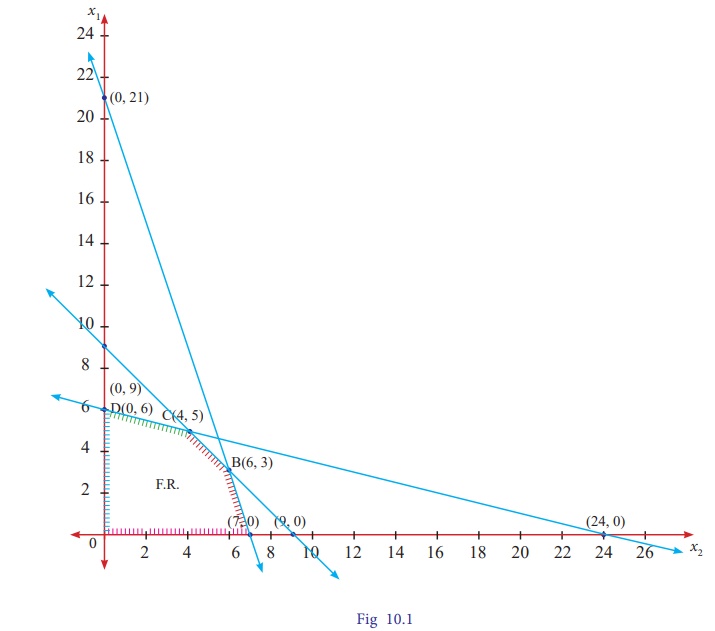
The feasible region satisfying
all the conditions is OABCD.The co-ordinates of the points are O(0,0)
A(7,0);B(6,3) [ the point B is the intersection of two lines x1+ x2= 9 and 3 x1+
x2= 21];C(4,5) [ the point
C is the intersection of two lines
x1+ x2 = 9 and x1+ 4x2 = 24] and D(0,6).
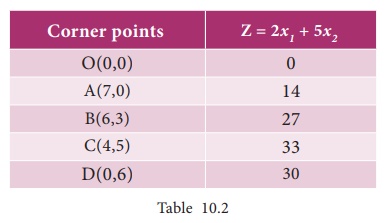
Maximum
value of Z occurs at C. Therefore the solution is x1 =4, x2
= 5, Z max = 33
Example 10.6
Solve the
following LPP by graphical method Minimize z
= 5x1+4x2 Subject to constraints 4x1+ x2 ≥ 40 ; 2x1+3x2 ≥ 90 and x1,
x2
> 0
Solution:
Since both the decision variables
x1 and x2 are non-negative, the
solution lies in the first quadrant of the plane.
Consider the equations 4x1+x2 = 40 and 2 x1+3 x2 = 90
4x1+x 2
= 40 is a line passing through the points (0,40) and (10,0).Any point lying on
or above the line 4x1+x2= 40 satisfies the
constraint 4x1+ x2 ≥ 40.
2x1+3x2
= 90 is a line passing through the points (0,30) and (45,0). Any point lying on
or above the line 2 x1+3x2= 90 satisfies the constraint
2x1+3x2 ≥ 90.
Draw the
graph using the given constraints.
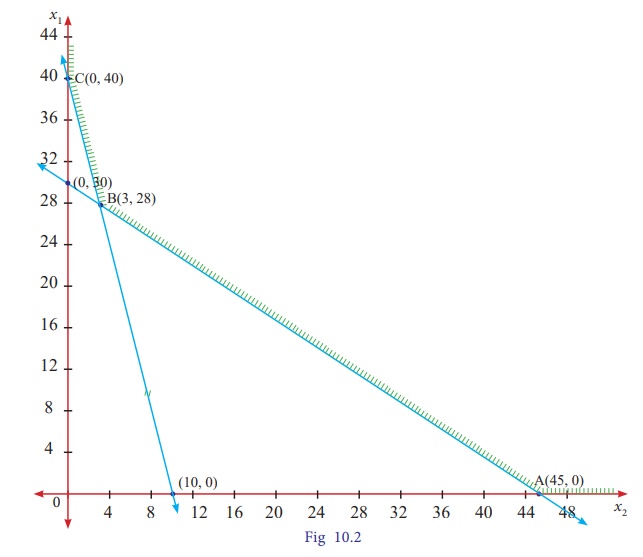
The
feasible region is ABC (since the problem is of minimization type we are moving
towards the origin.
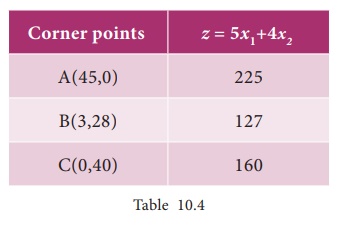
The minimum value of Z occurs at
B(3,28).
Hence the
optimal solution is x1 =
3, x2 = 28 and Zmin=127
Example 10.7
Solve the following LPP.
Maximize Z= 2 x1
+3x2 subject to
constraints x1 + x2 ≤ 30 ; x2 ≤ 12; x1 ≤ 20 and x1, x2≥ 0
Solution:
We find the feasible region using
the given conditions.
Since both the decision variables
x1 and x2 are non-negative, the
solution lies in the first quadrant of the plane.
Write all the inequalities of the
constraints in the form of equations.
Therefore we have the lines
x1+x2=30; x2 =12; x1= 20
x1+x2 =30 is a line passing
through the points (0,30) and (30,0)
x2 = 12 is a
line parallel to x1–axis
x1 = 20 is a
line parallel to x2–axis.
The
feasible region satisfying all the conditions x1+ x2≤
30; x2≤ 12 ; x1≤ 20 and x1, x2 ≥ 0 is
shown in the following graph.
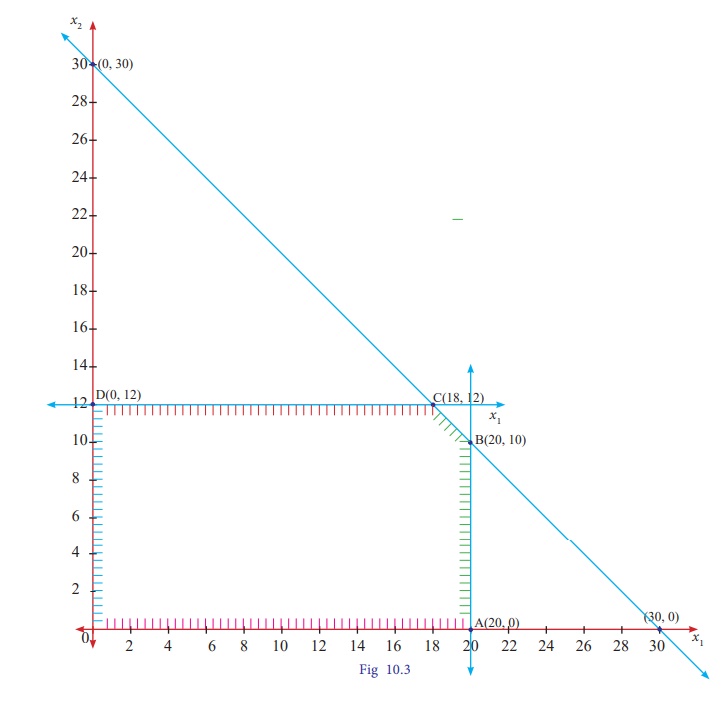
The feasible region satisfying
all the conditions is OABCD.
The
co-ordinates of the points are O(0,0) ; A(20,0); B(20,10) ; C(18,12) and
D(0,12).
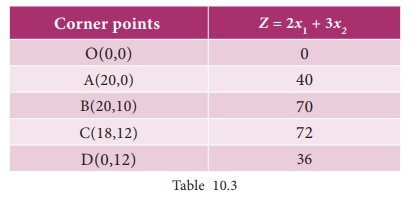
Maximum
value of Z occurs at C. Therefore the
solution is x1 = 18 , x2= 12, Z max = 72
Example 10.8
Maximize
Z = 3x1 + 4x2 subject to x1 – x2
< –1; –x1+x2 < 0 and x1, x2 ≥ 0
Solution:
Since both the decision variables
x1, x2 are non-negative ,the solution lies in the first
quadrant of the plane.
Consider the equations x1– x2 = –1 and – x1
+ x2 = 0
x1– x2 =–1 is a line passing through the points (0,1) and (–1,0)
–x1 + x2
= 0 is a line passing through the point (0,0)
Now we
draw the graph satisfying the conditions x1
– x2 < –1; –x1+x2 < 0 and x1,
x2≥0
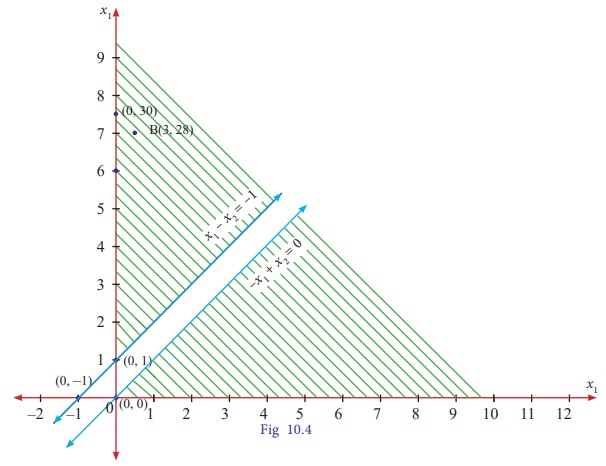
There is no common
region(feasible region) satisfying all the given conditions.
Hence the
given LPP has no solution.
Exercise 10.1
1. A
company produces two types of pens A and B. Pen A is of superior quality and
pen B is of lower quality . Profits on pens A and B are Rs 5 and Rs 3 per pen
respectively. Raw materials required for each pen A is twice as that of pen B.
The supply of raw material is sufficient only for 1000 pens per day . Pen A
requires a special clip and only 400 such clips are available per day. For pen
B, only 700 clips are available per day . Formulate this problem as a linear
programming problem.
2. A
company produces two types of products say type A and B. Profits on the two
types of product are Rs.30/- and Rs.40/- per kg respectively. The data on
resources required and availability of resources are given below.
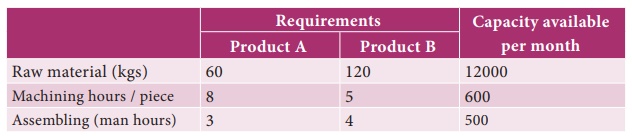
Formulate this problem as a
linear programming problem to maximize the profit.
3. A
company manufactures two models of voltage stabilizers viz., ordinary and
auto-cut. All components of the stabilizers are purchased from outside sources
, assembly and testing is carried out at company’s own works. The assembly and
testing time required for the two models are 0.8 hour each for ordinary and
1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is
available per week. The market for the two models has been surveyed which
suggests maximum weekly sale of 600 units of ordinary and 400 units of auto-cut
. Profit per unit for ordinary and auto-cut models has been estimated at Rs 100
and Rs 150 respectively. Formulate the linear programming problem.
4. Solve
the following linear programming problems by graphical method.
(i) Maximize
Z = 6x1 + 8x2 subject to constraints 30x1+20x2 ≤300;5x1+10x2 ≤110; and x1, x2 > 0 .
(ii)
Maximize Z = 22x1 +
18x2 subject to constraints 960x1 +
640x2 ≤ 15360 ; x1 +
x2 ≤ 20 and
x1 , x2 ≥ 0 .
(iii) Minimize
Z = 3x1 + 2x2
subject to the constraints 5x1+
x2≥10; x1+ x2≥6; x1+
4 x2 ≥12 and x1, x2≥0.
(iv) Maximize
Z = 40x1 + 50x2 subject to
constraints 30x1 + x2 ≤ 9 ; x1
+ 2x2 ≤ 8 and x1 ,
x2 ≥ 0
(v) Maximize
Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2
≤ 36 ; 5x1
+ 2x2 ≤ 50 ; 2x1 + 6x2
≤ 60 and x1 , x2
≥ 0
(vi) Minimize Z
= 20x1 + 40x2 subject to the constraints
36x1 + 6x2 ≥ 108, 3x1 + 12x2
≥ 36, 20x1 + 10x2 ≥ 100 and x1 , x2 ≥ 0
Related Topics