Critical path analysis

Critical path analysis

For each activity an estimate must be made of time that will be spent in the actual accomplishment of that activity. Estimates may be expressed in hours, days, weeks or any other convenient unit of time. The time estimate is usually written in the network immediately above the arrow. For the purpose of calculating various times of events and activities, the following terms shall be used in critical path calculations:

E_i = Earliest start time of event i

L_j = Latest start time of event j

t_ij = Duration of activity (i,j)

The next step after making the time estimates is the calculations which are done in the following ways:

(i) Forward Pass Calculations

(ii) Backward Pass Calculations.

Forward pass calculations:

We start from the initial node 1 with starting time of the project as zero. Proceed through the network visiting nodes in an increasing order of node number and end at the final node of the network. At each node, we calculate earliest start times for each activity by considering E_i as the earliest occurrence of node i.

The method may be summarized as below:

Step 1.                          Set E₁ = 0 ; i = 1 (initial node)

Step 2.                          Set the earliest start time(EST) for each activity that begins at node i as ES_ij = E_i ; for all activities (i, j) that start at node i.

Step 3.                          Compute the earliest finish time(EFT) of each activity that begins at node i by adding the earliest start time of the activity to the duration of the activity. Thus EF_ij = ES_ij + t_ij = E_i + t_ij

Step 4.                          Move on to next node, say node j(j > i) and compute the earliest start time at node j, using E_j = max i{EF}_ij , = max_i "{E_i + t_ij} , for all immediate predecessor activities.

Step 5.                          If j = n (final node), then the earliest finish time for the project is given by E_n = max {EF_ij }, = max {E_{n - 1} + t_ij },

Backward pass calculations:

We start from the final (last) node n of the network, proceed through the network visiting nodes in the decreasing order of node numbers and end at the initial node 1. At each node, we calculate the latest finish time and latest start time for each activity by considering L_j as the latest occurrence of node j. The method may be summarized below:

Step 1.                          L_n = E_n; for j = n

Step 2.                          Set the latest finish time (LFT)of each activity that ends at node j as LF_ij = L_j

Step 3.                          Compute the latest start time(LST) of all activities ending at node j, subtracting the duration of each activity from the latest finish time of the activity. Thus, LS_ij = LF_ij - t_ij = L_j - t_ij

Step 4.                          Proceed backward to the next node i( i<j) in the sequence and compute the latest occurrence time at node i using

L_i = min _j {LS_ij }, = min _j {L_j - t_ij },

Step 5.        If j = 1 (initial node), then  L₁ = min {LS_ij }, = min {L₂ - t_ij },

Critical path:

The longest path connected by the activities in the network is called the critical path. A path along which it takes the longest duration.

For the activity (i,j), to lie on the critical path, following conditions must be satisfied:

(i) E_i = L_i  and  E_j = L_j

(ii) E_j - E_i = L_j - L_i = t_ij

Example 10.13

Compute the earliest start time, earliest finish time ,latest start time and latest finish time of each activity of the project given below:

Solution:

Earliest start time (EST)and latest finish time(LFT) of each activity are given ithe following network.

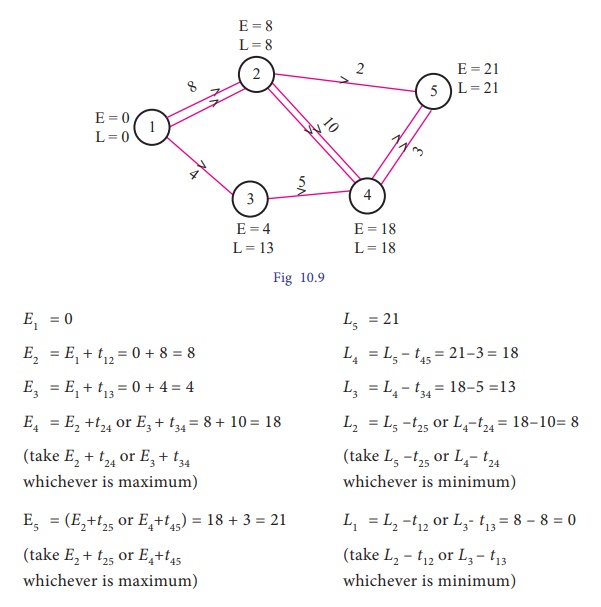
Here the critical path is 1-2-4-5, which is denoted by double lines.

The longest duration to complete this project is 21 days.

The path connected by the critical activities is the critical path(the longest path).

Critical path is 1-2-4-5 and project completion time is 21 days.

Example 10.14

Calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity of the project given below and determine the Critical path of the project and duration to complete the project.

Solution:

Here the critical path is 1–2–4–6

The project completion time is 25 weeks

Exercise 10.2

1. Draw the network for the project whose activities with their relationships are given below:

Activities A,D,E can start simultaneously; B,C>A; G,F>D,C; H>E,F.

2. Draw the event oriented network for the following data:

3. Construct the network for the projects consisting of various activities and their precedence relationships are as given below:

A,B,C can start simultaneously A<F, E; B<D, C; E, D<G

4. Construct the network for each the projects consisting of various activities and their precedence relationships are as given below:

5. Construct the network for the project whose activities are given below.

Calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity. Determine the critical path and the project completion time.

6. A project schedule has the following characteristics

Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

7. Draw the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

8. The following table gives the activities of a project and their duration in days

Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

9. A Project has the following time schedule

Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.

10. The following table use the activities in a construction projects and relevant information

Draw the network for the project ,calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration